モンティ・ホールの問題
確率は直感と異なる結果を返すことがあります.
本記事では,それが原因となり数学に物議を醸し出した問題である,モンティ・ホールの問題についてお話ししたいと思います.
モンティ・ホールの問題のきっかけは,アメリカのあるテレビ番組内のゲームです.
そのゲーム,及び,ゲームから生じた問題を簡単に説明すると以下のようになります.

問題.
扉が3つあり,1つはアタリ,2つはハズレである.ゲームのプレーヤーは扉のうち1つを選択する.その後,アタリの扉を知っている第三者(この番組では司会者)が,プレーヤーが選択しなかった2つの扉のうち,ハズレの扉を1つプレーヤーに教える.その後,プレーヤーは残った2つの扉のうち1つを選択し直すことができる.さて,プレーヤーは最初に選択した扉を変わらず選ぶべきだろうか?それとも選択を変更するべきだろうか?
実際のテレビ番組ではアタリの扉の向こうには景品の新車があり,ハズレの扉の向こうにはヤギが居たようです.
さて,物議を醸し出したのはここからです.
当時「世界で一番IQが高い人物」として知られていた女性のサバントが,ニュース雑誌のコラムで「選択する扉を変更すると当たる確率が2倍になる」という内容の記事を書きました.ちなみに,サバントの書いた記事の内容は正しく,選択を変えなかった場合に当たる確率は3分の1,変更した場合は3分の2です.
しかし後日,サバント宛に大量の投書が殺到しました.その内容の多くは「残った扉はアタリ1つとハズレ1つなのだから,確率は同じである」というものでした.反論の投書をした人物には,数学の博士号の所持者や現役の数学者も多くいました.中にはサバントを馬鹿にしたような内容や,侮辱的な内容の投書もありました.ちなみに,数学者の反論の一部はWikipediaや『放浪の天才数学者エルデシュ』の第6章で読むことができます.いかにサバントのことを見下しているかが分かる内容となっております.
また,偉大な数学者のひとりである,ポール・エルデシュも「確率は2分の1」だと反論しています1ここでは,失態のみを紹介していますが,エルデシュは歴史に残る数学者であり,風変わりな生活をしていたこと,共著論文が多いことで有名です.詳しくはポール・ホフマン著(平石律子訳)『放浪の天才数学者エルデシュ』を読むのが良いでしょう..
その後,サバントは何度か反論への反論をコラムに掲載しますが,反論の投書(もはや罵詈雑言,罵倒の類)は止まることがありませんでした.
事態が収束したのは,エルデシュの弟子がコンピュータでシミュレーションを行った結果,サバントの主張が正しいことが分かり,また,何名かの学者が解説を行った後でした.
ヒトは「直感に反するものは受け入れ難い」性質を持っていますし,ヒトは「何を言ったかより,誰が言ったかに影響を受けやすい」ものですが,これらが良くない方向に働いた結果,罵詈雑言飛び交う大論争になってしまいました2数学者はゲームのルールを理解していなかったのだから間違えるのも仕方がないと,誤った反論を強く(ときに品も無く)行った数学者を擁護する人もいるようですが,その場合だと,問題を理解せずに答えを出そうとする数学者が大量にいて,そのうちの何人かは人を当然のように見下すという,ひどい状況になってしまうのですが,そんな擁護の仕方でよろしいのでしょうか..
これが,モンティ・ホールの問題が引き起こした騒動の概要でした.
さて最後に,モンティ・ホールの問題において,なぜ選択を変更した方が良いのかを解説したいと思います.
最も分かりやすい説明は,場合分けを使ったものでしょう.
2つのハズレの扉を,ハズレ1とハズレ2として区別します.
初めの3択でアタリの扉を選んだ場合はどうなるでしょうか.
最初にアタリの扉を選んだ後,司会者からハズレ1かハズレ2の扉がハズレであることが教えられます.
この場合は,扉を変更するとハズレ,扉を変更しないとアタリとなります.
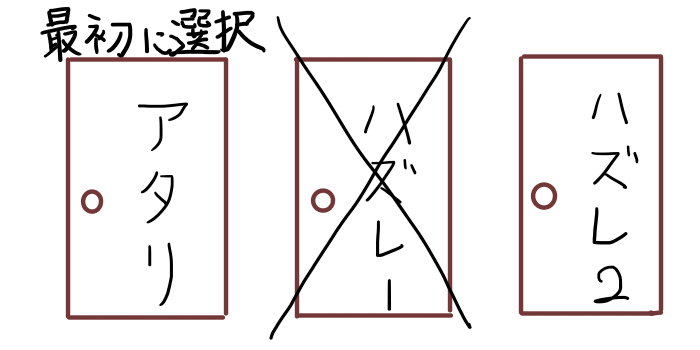
次に,最初の3択でハズレ1の扉を選んだ場合はどうなるでしょうか.
最初にハズレ1の扉を選んだ後,司会者からハズレ2の扉がハズレであることが教えられます.司会者は「ハズレの扉」しか教えませんから,ここではハズレ2が必ず候補から外れます.
この場合は,扉を変更するとアタリ,扉を変更しないとハズレとなります.
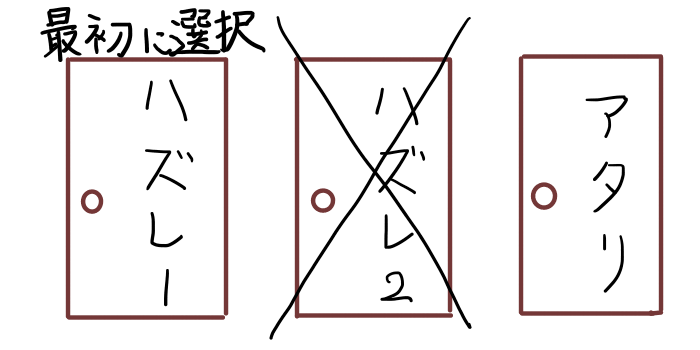
最後に,最初の3択でハズレ2の扉を選んだ場合を考えます.
最初にハズレ2の扉を選んだ後,司会者から,ハズレ1の扉がハズレであると教えられます.
この場合は,扉を変更するとアタリ,扉を変更しないとハズレとなります.
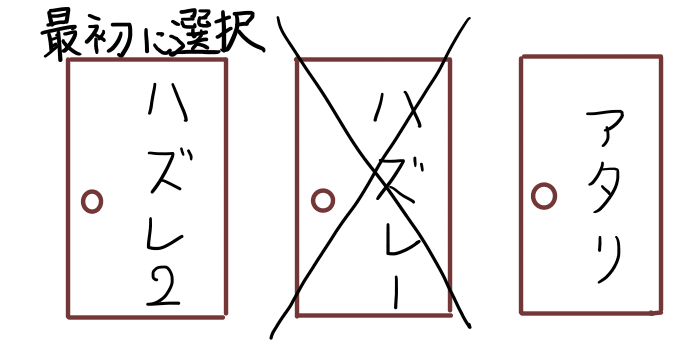
以上のことをまとめると,最初の扉の3択で,どの扉を選ぶことも同様に確からしいならば,選択を変更した場合のアタリの確率は3分の2,変更しなかった場合にアタリとなる確率は3分の1となります.
参考文献