三角形の五心　〜性質と証明〜

本記事では，三角形の五心について解説を行います．
ここで書かれる命題の証明は，証明方法のほんの一例にすぎませんので，ぜひ自分なりの証明に挑戦してみてください．
また，中学校で習う定理・命題に関しましては，図を省略していることがあります．分かりにくい場合は，ぜひ自分で図を描いてみてください．

外心

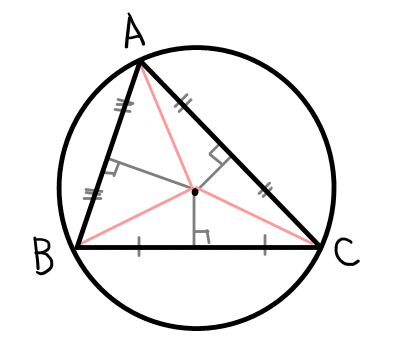
外心の押さえておきたいポイントは以下の3点です．

• 三角形の外接円の中心である．
• 三角形の3つの辺の垂直二等分線は1点(外心)で交わる．
• 外心から各頂点までの距離は等しい．

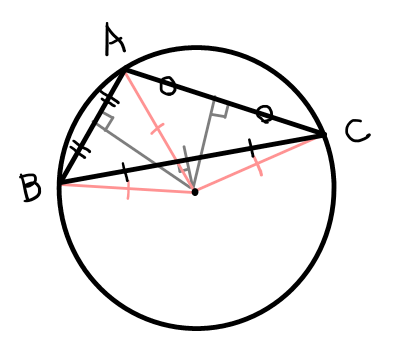
下の図のように外心が三角形の外にある場合もあります．

それでは先ほど書いた3つのポイントは一度忘れて，それぞれの性質が成り立つか確かめてみましょう．

重要な定理を証明するために，まずは垂直二等分線に関する以下の命題を証明します．

命題．
線分$\mathrm{AB}$と点$\mathrm{P}$が存在するとき，点$\mathrm{P}$が線分$\mathrm{AB}$の垂直二等分線上にあるならば，$\mathrm{AP} = \mathrm{BP}$が成り立つ．

証明．
線分$\mathrm{AB}$の中点を$\mathrm{M}$とする．
線分$\mathrm{PM}$は共通しており，中点なので$\mathrm{AM} = \mathrm{BM}$，$\angle \mathrm{PMA} = \angle \mathrm{PMB}$より，2辺と間の角が等しいので，
$\bigtriangleup \mathrm{AMP} \equiv \bigtriangleup \mathrm{BMP}$
よって，
$\mathrm{AP} = \mathrm{BP}$

先ほどの命題の逆も成り立ちます．

命題．
線分$\mathrm{AB}$と点$\mathrm{P}$が存在するとき，$\mathrm{AP} = \mathrm{BP}$が成り立つならば，点$\mathrm{P}$が線分$\mathrm{AB}$の垂直二等分線上にある．

証明．
線分$\mathrm{AB}$の中点を$\mathrm{M}$とする．
$\mathrm{P} = \mathrm{M}$ならば，$\mathrm{P}$は垂直二等分線上の点である．
$\mathrm{P} \neq \mathrm{M}$の場合，
$\mathrm{AP} = \mathrm{BP}$，$\mathrm{AM} = \mathrm{BM}$，$\mathrm{PM}$は共通より，3辺が等しいため，
$\bigtriangleup \mathrm{AMP} \equiv \bigtriangleup \mathrm{BMP}$
となる．よって$\angle \mathrm{AMP} = \angle \mathrm{BMP}$かつ，$\angle \mathrm{AMP} + \angle \mathrm{BMP} = 180^{\circ}$より，$\angle \mathrm{AMP} = \angle \mathrm{BMP}=90^{\circ}$
つまり
$\mathrm{AB} \perp \mathrm{PM}$
したがって，点$\mathrm{P}$は垂直二等分線上の点である．

それでは，外心に関わる命題を証明していきましょう．

定理．¹命題の中でも特に重要なものを「定理」と呼びます．
三角形の3辺の垂直二等分線は1点で交わる．

証明．
$\bigtriangleup \mathrm{ABC}$の辺$\mathrm{AB}$と辺$\mathrm{BC}$の垂直二等分線の交点を$\mathrm{O}$とする．辺$\mathrm{AB}$の中点を$\mathrm{M}$，辺$\mathrm{BC}$の中点を$\mathrm{M}^{\prime}$とすると，
$\bigtriangleup \mathrm{AMO} \equiv \bigtriangleup \mathrm{BMO}$
$\bigtriangleup \mathrm{BM^{\prime}O} \equiv \bigtriangleup \mathrm{CM^{\prime}O}$
よって，
$\mathrm{OA} = \mathrm{OB}$
$\mathrm{OB} = \mathrm{OC}$
が成り立つ．したがって，
$\mathrm{OA} = \mathrm{OC}$
も成り立つ．よって，$\mathrm{O}$は辺$\mathrm{CA}$の垂直二等分線上にあり，3辺の垂直二等分線が1点で交わることが示された．

ちなみに$\mathrm{OA} = \mathrm{OB} = \mathrm{OC}$より，$\mathrm{O}$を中心とした$\bigtriangleup \mathrm{ABC}$の外接円が存在することが分かります．

内心

内心の押さえておきたいポイントは以下の3点です．

• 三角形の内接円の中心である．
• 三角形の3つの内角の二等分線は1点(内心)で交わる．
• 内心から各辺までの距離は等しい．

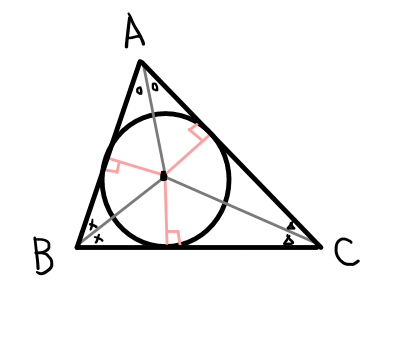
外心のときと同様に，先ほど書いた3つのポイントは一度忘れて，それぞれの性質が成り立つか確かめてみましょう．

まずは外心のときと同様に，重要な定理につながる命題を証明します．

命題．
同一平面上に半直線$\mathrm{OA}$と$\mathrm{OB}$が存在するとき，$\angle \mathrm{AOB}$の二等分線上の点$\mathrm{P}$から半直線$\mathrm{OA}$，$\mathrm{OB}$への距離は等しい．

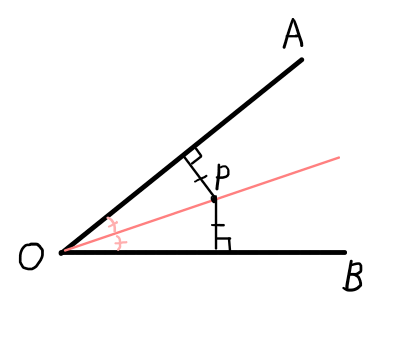
証明．
半直線$\mathrm{OA}$と点$\mathrm{P}$から$\mathrm{OA}$への垂線との交点を点$\mathrm{D}$，同様に，半直線$\mathrm{OB}$と点$\mathrm{P}$から$\mathrm{OB}$への垂線との交点を点$\mathrm{E}$とする．
点$\mathrm{P}$は$\angle \mathrm{AOB}$の二等分線上にあるため，
$\angle \mathrm{DOP} = \angle \mathrm{EOP}$
また，辺$\mathrm{OP}$は共有しており，$\angle \mathrm{ODP} = \angle \mathrm{OEP} = 90^{\circ}$なので，
$\bigtriangleup \mathrm{OPD} \equiv \bigtriangleup \mathrm{OPE}$
よって，
$\mathrm{PD} = \mathrm{PE}$

少しだけ条件を追加すれば，その逆も成り立ちます．

命題．
$\angle \mathrm{AOB}$の内側に点$\mathrm{P}$があり，半直線$\mathrm{OA}$，$\mathrm{OB}$との距離が等しいとき，点$\mathrm{P}$は$\angle \mathrm{AOB}$の二等分線上に存在する．

証明．
半直線$\mathrm{OA}$と点$\mathrm{P}$から$\mathrm{OA}$への垂線との交点を点$\mathrm{D}$，同様に，半直線$\mathrm{OB}$と点$\mathrm{P}$から$\mathrm{OB}$への垂線との交点を点$\mathrm{E}$とする．
$\bigtriangleup \mathrm{OPD}$ と $\bigtriangleup \mathrm{OPE}$において，三平方の定理より，
$\mathrm{OD}^2 = \mathrm{OP}^2 - \mathrm{PD}^2$
$\mathrm{OE}^2 = \mathrm{OP}^2 - \mathrm{PE}^2$
前提条件より$\mathrm{PD} = \mathrm{PE}$なので，
$\mathrm{OD} = \mathrm{OE}$
対応する3辺が等しいので，
$\bigtriangleup \mathrm{OPD} \equiv \bigtriangleup \mathrm{OPE}$
よって，
$\angle \mathrm{POD} = \angle \mathrm{POE}$
したがって，点$\mathrm{P}$は$\angle \mathrm{AOB}$の二等分線上に存在する．

定理．
$\bigtriangleup \mathrm{ABC}$の3つの角の二等分線は１点で交わる．

証明．
$\bigtriangleup \mathrm{ABC}$の$\angle \mathrm{B}$の二等分線と$\angle \mathrm{C}$の二等分線の交点を$\mathrm{I}$とする．$\mathrm{I}$から各辺へ垂線をおろし，辺$\mathrm{AB}$との交点を$\mathrm{D}$，辺$\mathrm{BC}$との交点を$\mathrm{E}$，辺$\mathrm{AC}$との交点を$\mathrm{F}$とする．
$\bigtriangleup \mathrm{BDI} \equiv \bigtriangleup \mathrm{BEI}$，
$\bigtriangleup \mathrm{CEI} \equiv \bigtriangleup \mathrm{CFI}$
よって，
$\mathrm{ID} = \mathrm{IE} = \mathrm{IF}$
したがって，$\angle \mathrm{A}$の二等分線も点$\mathrm{I}$を通り，3つの角の二等分線は1点で交わる．

さらに，中心が$\mathrm{I}$で3点$\mathrm{D}$，$\mathrm{E}$，$\mathrm{F}$で接する$\bigtriangleup \mathrm{ABC}$の内接円が存在することが分かります．

この定理はチェバの定理の逆を使った証明もできます．チェバの定理の逆についてはこちらの記事をご覧ください．

チェバの定理・メネラウスの定理

重心

重心の押さえておきたいポイントは以下の2点です．

• 三角形の3つの中線は1点(重心)で交わる．
• 重心は各中線を$2:1$に内分する．

三角形の各頂点と対辺の中点を結ぶ線を中線といいます．

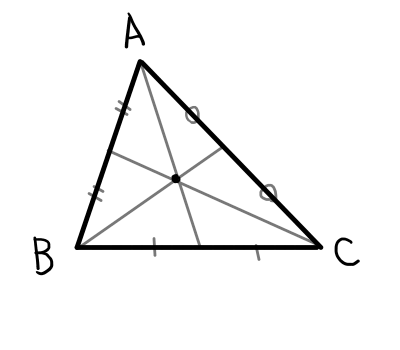
これからの証明で中点連結定理を使うので，簡単におさらいしたいと思います．

中点連結定理
$\bigtriangleup \mathrm{ABC}$において，辺$\mathrm{AB}$の中点を$\mathrm{M}$，辺$\mathrm{AC}$の中点を$\mathrm{N}$とすると，以下の2つが成り立つ．
$\mathrm{BC} /\!/ \mathrm{MN}$
$\mathrm{BC} = 2\mathrm{MN}$

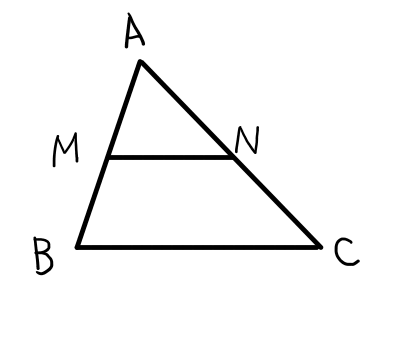
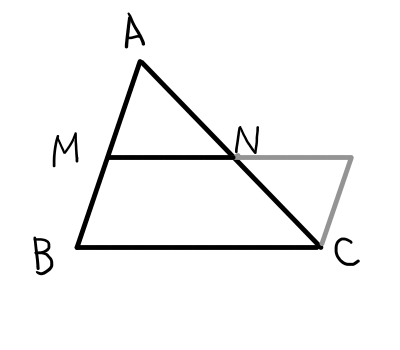
相似を使うと楽に証明ができそうですが，論理の堂々巡りを避けるために，平行四辺形と合同を利用して証明するのが筋の良いやり方です．中学校で学習済みだと思いますので，証明は省略します²下の図を見れば証明方法も分かると思います．．

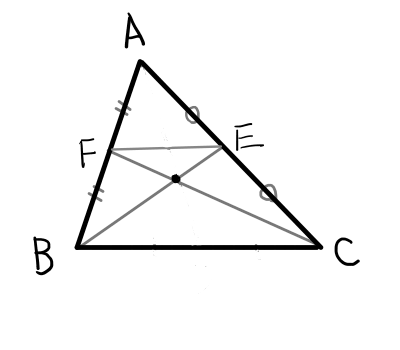
まずは，2つの中線の交点が中線を$2:1$に内分することを示します．

定理．
$\bigtriangleup \mathrm{ABC}$の中線の交点は，中線を$2:1$に内分する．

証明．
辺$\mathrm{AB}$の中点を$\mathrm{F}$，辺$\mathrm{AC}$の中点を$\mathrm{E}$とし，中線$\mathrm{BE}$と中線$\mathrm{CF}$の交点を$\mathrm{G}$とする．
中点連結定理より
$\mathrm{BC} /\!/ \mathrm{EF}$
$\mathrm{BC} = 2\mathrm{EF}$
このことから，$\bigtriangleup \mathrm{BCG} \text{∽} \bigtriangleup \mathrm{EFG}$であり，相似比は$2 : 1$である．よって，
$\mathrm{CG} : \mathrm{FG} = \mathrm{BG} : \mathrm{EG} = 2 : 1$

次に三角形の3つの中線が1点で交わることを証明します．

定理．
$\bigtriangleup \mathrm{ABC}$の3つの中線は１点で交わる．

証明．
辺$\mathrm{AB}$の中点を$\mathrm{F}$，辺$\mathrm{AC}$の中点を$\mathrm{E}$，辺$\mathrm{BC}$の中点を$\mathrm{D}$とし，中線$\mathrm{BE}$と中線$\mathrm{CF}$の交点を$\mathrm{G}$，中線$\mathrm{AD}$と中線$\mathrm{BE}$の交点を$\mathrm{G^{\prime}}$とする．
中点連結定理より
$\bigtriangleup \mathrm{ABG^{\prime}} \text{∽} \bigtriangleup \mathrm{DEG^{\prime}}$であり，相似比は$2 : 1$である．よって，
$\mathrm{BG^{\prime}} : \mathrm{EG^{\prime}} = 2 : 1$
前の定理の証明より，$\mathrm{BG} : \mathrm{EG} = 2 : 1$でもあるため，$\mathrm{G}$と$\mathrm{G^{\prime}}$は同一の点である．よって，3つの中線は1点で交わる．

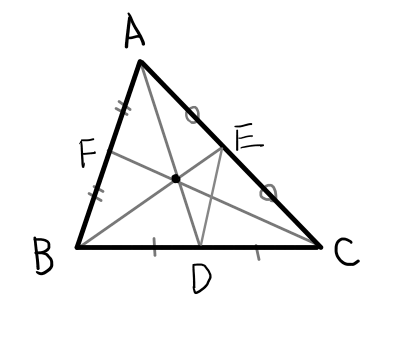
垂心

垂心の定義は以下の通りです．

各頂点から対辺への垂線は1点で交わり，その点を垂心という．

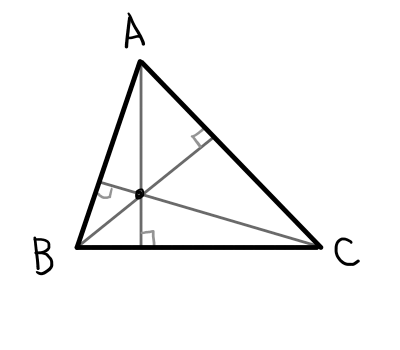
ここでは各頂点から対辺への垂線が1点で交わることを証明したいと思います．

定理．
$\bigtriangleup \mathrm{ABC}$の各頂点から対辺への垂線は１点で交わる．

証明．

頂点$\mathrm{A}$から対辺$\mathrm{BC}$におろした垂線と対辺との交点を$\mathrm{D}$，頂点$\mathrm{B}$から対辺$\mathrm{ AC}$におろした垂線と対辺との交点を$\mathrm{E}$，頂点$\mathrm{C}$から対辺$\mathrm{AB}$におろした垂線と対辺との交点を$\mathrm{F}$とする．
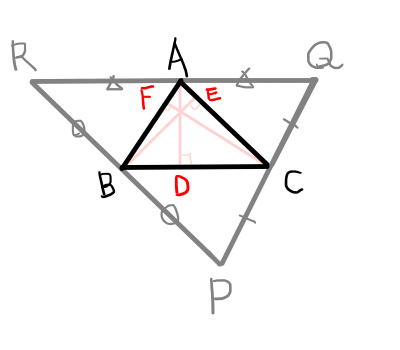
また，各頂点から，対辺に平行で対辺と同じ長さの線分を頂点の両側に引き，下の図のような$\bigtriangleup \mathrm{PQR}$を作る．
$\bigtriangleup \mathrm{ABC}$の垂線は$\bigtriangleup \mathrm{PQR}$の垂直二等分線となるため，その交点は$\bigtriangleup \mathrm{PQR}$の外心となる．よって3本の垂線は1点で交わる．

他にも，外接円を持つ四角形を利用する証明方法などがあります．

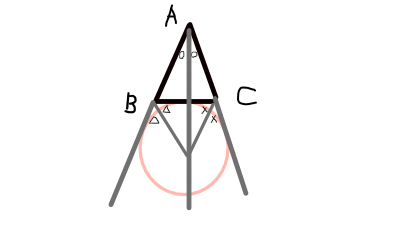
傍心

• 1つの頂点の内角の二等分線と，他の2つの頂点の外角の二等分線は1点で交わる．この点を傍心という．
• 傍心は3つある．
• 傍心を中心とし，対辺と接し，他の2辺を延長した直線と接する円が描ける．この円のことを傍心円という．

図を描くと以下のようになります．少し雑な図ですみません．

最後になりますが，次の命題の証明を演習問題として残そうと思います．
ここまでの証明と流れは大きく変わりません．ここまでの内容を理解している人ならすぐに証明できるはずです．

定理．
$\bigtriangleup \mathrm{ABC}$において$\angle \mathrm{A}$の内角の二等分線と，$\angle \mathrm{B}$の外角の二等分線と，$\angle \mathrm{C}$の外角の二等分線は1点で交わる．

ヒント³傍心から対辺$\mathrm{BC}$，半直線$\mathrm{AB}$，$\mathrm{AC}$への垂線を引いてみましょう．そのあとは，合同な図形を利用すれば証明できます．

　　

「勝手気ままに高校数学」シリーズ一覧へ