三角関数の基礎 〜三角関数の導入とsin,cos,tanの関係〜
前回,前々回の記事で一般角と弧度法について解説しましたので,本記事ではいよいよ三角関数を解説したいと思います.などと仰々しく書いてみましたが,0^{\circ} \leqq \theta \leqq 180^{\circ} の範囲に拡張された三角比とほとんど変わらないので,気楽に読んでください.
先にネタバラシをすると,\sin,\cos,\tan を一般角まで拡張したものを,まとめて三角関数といいます.
またこれ以降の記事においては,特に断りがない場合,角度の大きさは弧度法により表します.
途中に演習問題もありますが,弧度法に慣れるための練習だと考えてください.
↓前々回の記事↓
↓前回の記事↓
三角関数の定義
xy座標において,原点\mathrm{O}を中心とする半径rの円を描きます.
x軸の正の側を始線とし,\thetaの動径と円の交点を\mathrm{P},また\mathrm{P}の座標を(x, y)とします.
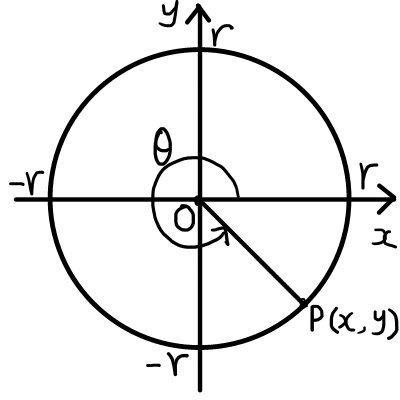
このとき,一般角の正弦1\sin(sine,サイン),余弦2\cos(cosine,コサイン),正接3\tan(tangent,タンジェント)を以下のように定義します.
\begin{aligned} \sin{\theta} &= \frac{y}{r} \\ \\ \cos{\theta} &= \frac{x}{r} \\ \\ \tan{\theta} &= \frac{y}{x} (ただし,\theta = \frac{\pi}{2} + n \pi (nは整数)のとき定義しない) \end{aligned}
数学Ⅰで学習した三角比を一般角に当てはめただけで,形は変わっていません.
また,これら3つの関数をまとめて三角関数といいます.
また定義より,次のことが直ちに導かれます.
\begin{aligned} y = r \sin{\theta} \\ x = r \cos{\theta}\\ \end{aligned}
ここで三角関数の値域について考えてみましょう.
三角関数の値域はそれぞれ以下のようになります.
-1 \leqq \sin{\theta} \leqq 1
-1 \leqq \cos{\theta} \leqq 1
\tan{\theta}は全ての実数を取りうる.
単位円を用いた値の求め方
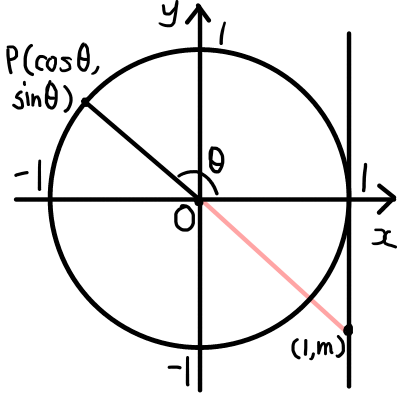
三角関数の値を素早く求める方法として,単位円を用いる方法があります.単位円とは,半径1の円のことです.
単位円を用いると,
\begin{aligned}
\sin{\theta} = y \\
\cos{\theta} = x \\
\tan{\theta} = \frac{y}{x}
\end{aligned}
となります.また,\tan{\theta}は,\thetaの動径を直線とみなしたものとx=1との交点の座標を(1, m)とすることで,\tan{\theta}=mとすることもできます.
演習問題
角度\thetaが以下の値をとるとき,\sin{\theta},\cos{\theta},\tan{\theta}の値を求めよ.
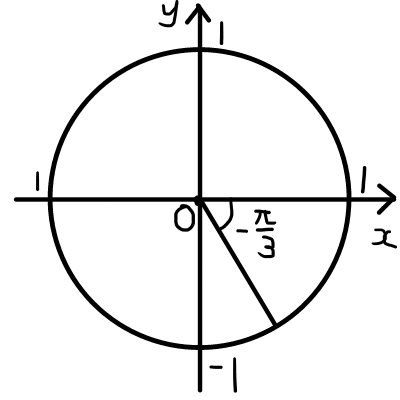
(1)\begin{aligned} - \frac{\pi}{3} \end{aligned}
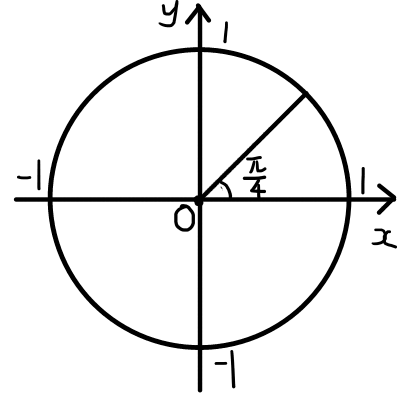
(2)\begin{aligned} \frac{\pi}{4} \end{aligned}
(3)\begin{aligned} \frac{5}{6} \pi \end{aligned}
(4)\begin{aligned} \frac{7}{6} \pi \end{aligned}
解答例と解説
(1)
\begin{aligned}
\sin{\left( - \frac{\pi}{3} \right)} &= - \frac{\sqrt{3}}{2} \\
\\
\cos{\left( - \frac{\pi}{3} \right)} &= \frac{1}{2} \\
\\
\tan{\left( - \frac{\pi}{3} \right)} &= - \sqrt{3}
\end{aligned}
(2)
\begin{aligned}
\sin{\frac{\pi}{4}} &= \frac{1}{\sqrt{2}} \\
\\
\cos{\frac{\pi}{4}} &= \frac{1}{\sqrt{2}} \\
\\
\tan{\frac{\pi}{4}} &= 1
\end{aligned}
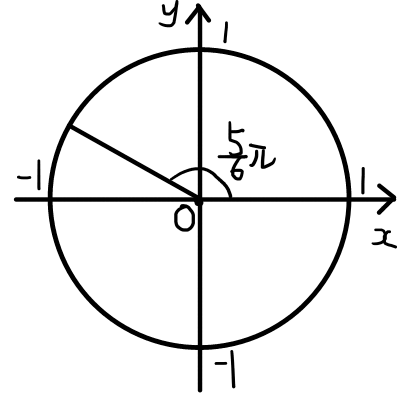
(3)
\begin{aligned}
\sin{\frac{5}{6} \pi } &= \frac{1}{2} \\
\\
\cos{\frac{5}{6} \pi} &= - \frac{\sqrt{3}}{2} \\
\\
\tan{\frac{5}{6} \pi} &= - \frac{1}{\sqrt{3}}
\end{aligned}
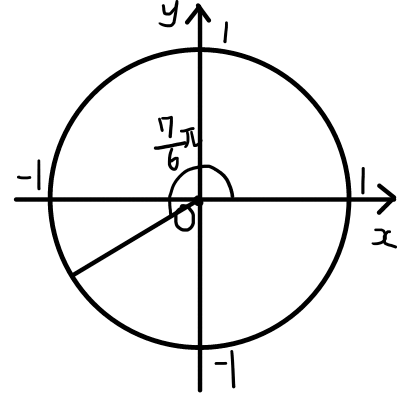
(4)
\begin{aligned}
\sin{\frac{7}{6} \pi } &= - \frac{1}{2} \\
\\
\cos{\frac{7}{6} \pi } &= - \frac{\sqrt{3}}{2} \\
\\
\tan{\frac{7}{6} \pi } &= \frac{1}{\sqrt{3}}
\end{aligned}
三角関数の関係
最後に,数学Ⅰの三角比で成り立っていた以下の3つの式が,三角関数においても成り立つか調べてみましょう.
(1)
\begin{aligned}
\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}
\end{aligned}
(2)
\begin{aligned}
\sin^2{\theta} + \cos^2{\theta} = 1
\end{aligned}
(3)
\begin{aligned}
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}\\
\end{aligned}

(1)について
半径rの円において,
\begin{aligned}
\tan{\theta} &= \frac{y}{x} \\
&= \frac{y}{r} \div \frac{x}{r} \\
&= \frac{\sin{\theta}}{\cos{\theta}}
\end{aligned}
ただし,分母が0にならないように\cos{\theta} \neq 0であり,また\theta \neq \frac{\pi}{2} + n \pi(nは整数)のとき\tan{\theta} は定義されていないことから,\theta \neq \frac{\pi}{2} + n \pi(nは整数)のとき(1)は成り立つ.
(2)について
\begin{aligned}
\sin^2{\theta} + \cos^2{\theta} &= \left( \frac{y}{r} \right)^2 + \left( \frac{x}{r} \right)^2 \\
&= \frac{x^2 + y^2}{r^2}
\end{aligned}
\thetaの動径と円の交点は,円x^2 + y^2 = r^2上の点であるため,
\begin{aligned}
\sin^2{\theta} + \cos^2{\theta} &= \frac{x^2 + y^2}{r^2} \\
&= \frac{r^2}{r^2} \\
&= 1
\end{aligned}
(3)について
\cos{\theta} \neq 0のとき(2)の両辺を\cos^2{\theta}で割って,
\begin{aligned}
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}
\end{aligned}
この式は\cos{\theta} \neq 0,つまり\theta \neq \frac{\pi}{2} + n \pi(nは整数)のとき成り立つ.

