整式の割り算
「整式」という名前の由来は,整数と似た性質を持っていることでしょう.
数学Ⅰでは,整式の足し算,引き算,掛け算を扱いました.
数学Ⅱではそれらに加えて,整式の割り算を学習します1先に断っておきますが,組立除法は扱いません.所謂受験テクニックのようなものにしか見えないためです.本質がありませんし,楽しくもありません.「みそじ(みはじ)の円」などと同じカテゴリーです..
整式の割り算
3x^3 -2x + 1をx - 2で割ってみましょう.
筆算で解くのが一般的です.筆算の方法は,整数の割り算の筆算に似ています.
今回の場合,割られる整式には2次の項がありませんので,2次の項の分だけ隙間を空けておきましょう.
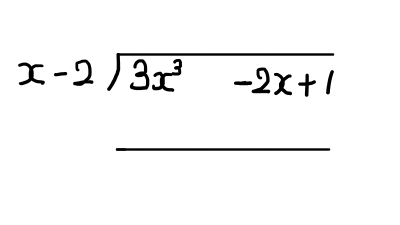
3x^3を消すために,x - 2に3x^2を掛けます.
その後引き算を行うのは,整数の割り算と同じです.
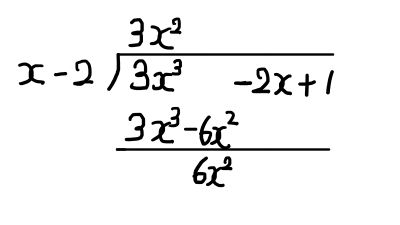
次の次数を降ろして,後はこれまでの手順の繰り返しです.
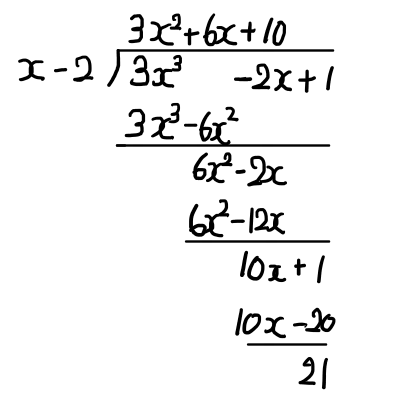
3x^3 -2x + 1をx - 2で割った商は 3x^2 + 6x + 10 余りは 21 となります.
整式の割り算
割られる整式をA,割る整式をB,商をQ,余りをRとすると,以下の式が成り立ちます.
A = BQ + Rただし余りはRの次数は,Aの次数より小さくなります.
余りがR = 0のとき,AはBで割り切れるといいます.

