チェバの定理・メネラウスの定理

本記事では，チェバの定理とメネラウスの定理の証明をします．

チェバの定理

チェバの定理．
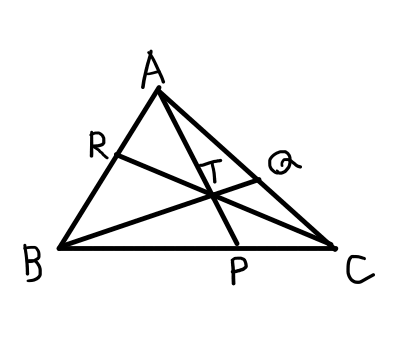
三角形$\bigtriangleup \mathrm{ABC}$の内部に点$\mathrm{T}$をとる．直線$\mathrm{AT}$と辺$\mathrm{BC}$の交点を$\mathrm{P}$，直線$\mathrm{BT}$と辺$\mathrm{CA}$の交点を$\mathrm{Q}$，直線$\mathrm{CT}$と辺$\mathrm{AB}$の交点を$\mathrm{R}$とすると，以下の等式が成り立つ．
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$

証明．
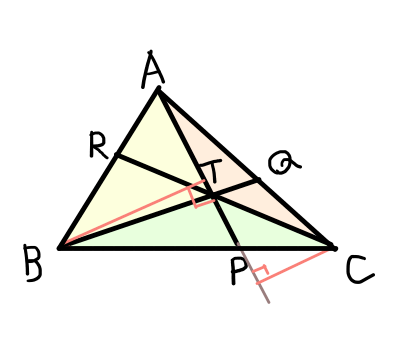
$\bigtriangleup \mathrm{ABT}$の面積を$S_1$，$\bigtriangleup \mathrm{BCT}$の面積を$S_2$，$\bigtriangleup \mathrm{CAT}$の面積を$S_3$とする．
$\bigtriangleup \mathrm{ABT}$の面積$S_1$と$\bigtriangleup \mathrm{CAT}$の面積$S_3$の面積比について考えると，底辺を共通する辺である$\mathrm{AT}$とすると，高さはそれぞれ頂点$\mathrm{B}$から$\mathrm{AT}$への垂線と高さは頂点$\mathrm{C}$から$\mathrm{AT}$への垂線となる．それぞれの垂線の足を$\mathrm{D}$，$\mathrm{E}$とすると，
$\bigtriangleup \mathrm{BDP}\text{∽}\bigtriangleup \mathrm{CEP}$より，
$\mathrm{BD}:\mathrm{CE} = \mathrm{BP}:\mathrm{PC}$
したがって，
$\frac{S_1}{S_3} = \frac{\mathrm{BP}}{\mathrm{PC}}$
となる．
同様の方法で，
$\frac{S_3}{S_2} = \frac{\mathrm{AR}}{\mathrm{RB}}$
$\frac{S_2}{S_1} = \frac{\mathrm{CQ}}{\mathrm{QA}}$
が求められる．
したがって，
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{S_1}{S_3} \cdot \frac{S_3}{S_2} \cdot \frac{S_2}{S_1} = 1$

チェバの定理の逆

チェバの定理の逆を証明したいと思います¹「逆」といいながら，厳密には，完全に逆の命題ではありません．．

チェバの定理の逆．
三角形$\bigtriangleup \mathrm{ABC}$において，辺$\mathrm{BC}$上に点$\mathrm{P}$があり，辺$\mathrm{CA}$上に点$\mathrm{Q}$があり，辺$\mathrm{AB}$上に点$\mathrm{R}$があるとする．以下の等式
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$
が成り立つならば，直線$\mathrm{AP}$，$\mathrm{BQ}$，$\mathrm{CR}$は一点で交わる．

証明．
2直線$\mathrm{AP}$，$\mathrm{BQ}$の交点を$\mathrm{T}$とする．直線$\mathrm{CT}$と$\mathrm{AB}$の交点を$\mathrm{R^{\prime}}$とすると，チェバの定理より，
$\frac{\mathrm{AR^{\prime}}}{\mathrm{R^{\prime}B}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$
が成り立つ．
条件の等式$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$より，
$\frac{\mathrm{AR}}{\mathrm{RB}}= \frac{\mathrm{AR^{\prime}}}{\mathrm{R^{\prime}B}}$
$\mathrm{R} = \mathrm{R^{\prime}}$となるため，3直線は1点で交わる．

演習．
チェバの定理の逆を用いて，三角形の3本の中線が1点で交わることを証明せよ．

三角形の3本の中線の交点とは重心のことです．詳しくはこちらのページをご覧ください．

三角形の五心　〜性質と証明〜

メネラウスの定理

メネラウスの定理．
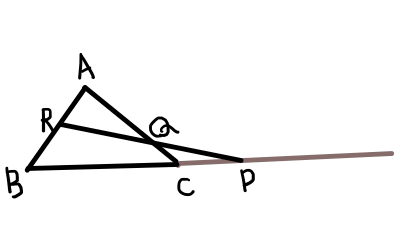
三角形$\bigtriangleup \mathrm{ABC}$に対して直線を一本引く．直線と辺$\mathrm{BC}$，辺$\mathrm{CA}$，辺$\mathrm{AB}$，もしくはその延長との交点を，点$\mathrm{P}$，$\mathrm{Q}$，$\mathrm{R}$とすると，以下の等式が成り立つ．
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$

証明．
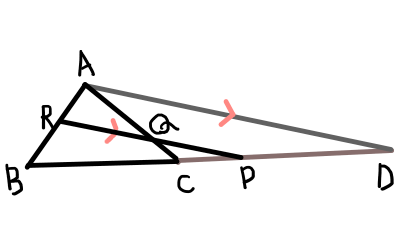
以下の図のように，点$\mathrm{A}$を通り，$\mathrm{RP}$と平行な直線を引く．その直線と，$\mathrm{BP}$の延長の交点を$\mathrm{D}$とすると，
$\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{PD}}{\mathrm{PB}}$
$\frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\mathrm{CP}}{\mathrm{PD}}$
となるので，
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\mathrm{PD}}{\mathrm{PB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CP}}{\mathrm{PD}} = 1$

メネラウスの定理の逆

メネラウスの定理の逆．
$\bigtriangleup \mathrm{ABC}$の辺$\mathrm{BC}$の延長線上に点$\mathrm{P}$，辺$\mathrm{CA}$上に点$\mathrm{Q}$，辺$\mathrm{AB}$上に点$\mathrm{R}$があるとき，以下の等式，
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$
が成り立つならば，点$\mathrm{P}$，$\mathrm{Q}$，$\mathrm{R}$は同一直線上にある．

証明．
点$\mathrm{P}$，$\mathrm{Q}$を通る直線と辺点$\mathrm{AB}$との交点を点$\mathrm{R^{\prime}}$とすると，
$\frac{\mathrm{AR^{\prime}}}{\mathrm{R^{\prime}B}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$
が成り立つ．
また，条件より，
$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1$
が成り立つため，
$\frac{\mathrm{AR}}{\mathrm{RB}}= \frac{\mathrm{AR^{\prime}}}{\mathrm{R^{\prime}B}}$
$\mathrm{R} = \mathrm{R^{\prime}}$となり，3点$\mathrm{P}$，$\mathrm{Q}$，$\mathrm{R}$は同一直線上の点となる．

　

「勝手気ままに高校数学」シリーズ一覧へ