データの分析の基本用語と定理

近年はデータ分析が盛んになっています．AI¹近い分野の研究をしているのに定義がわからない謎ワードだとかも流行っているようですね．
そんな時流であるためか，中学高校の「数学」や「情報」において，データを扱う単元は，学習指導要領が変更されるたびに増加しています．令和4年度入学の学生から適用される学習指導要領では，高校で仮説検定を扱うようになり，令和7年度大学入試からは，大学入学共通テストの「情報Ⅰ」が国立大学の受験に必須の科目となりました．

この記事では，「データの分析」の単元の基本用語を紹介したいと思います．

平均

変量xのn個の実際のデータをx_1, x_2, \cdots , x_nとします．このとき，xの平均 \bar{x}を以下のように定義します．

平均の定義．
変量xのn個のデータx_1, x_2, \cdots , x_nの平均 \bar{x}は，
\begin{aligned} \bar{x} &= \frac{x_1 + x_2 + \cdots + x_n}{n} \\ &= \frac{1}{n} \sum_{i=1}^{n} x_i \end{aligned}

式の1行目と2行目は同じことを書いています．
2行目の方がコンパクトにまとまりますので，総和の記号\Sigmaが分からない人はこちらの記事を読んでみて下さい．

総和Σと総乗Π

平均の計算の例を挙げてみましょう．5人の英語のテストの点数をそれぞれ，51，72，93，80，64とすると，その平均は，
\begin{aligned} \bar{x} &= \frac{51 + 72 + 93 + 80 + 64}{5} \\ &= \frac{360}{5} \\ &= 72 \end{aligned}
となります．

愚直に計算すると大変なので，数字が大きい場合は仮平均を用いて計算するのが一般的です．

仮平均を用いた平均の求め方
n個のデータx_1, x_2, \cdots , x_nの平均 \bar{x}を求める．仮平均の値をmとすると，
\begin{aligned} \bar{x} &= m + \frac{(x_1 - m) + (x_2 - m) + \cdots + (x_n - m)}{n} \\ &= m + \frac{1}{n} \sum_{i=1}^{n} (x_i - m) \end{aligned}

証明．
\begin{aligned} &　m + \frac{1}{n} \sum_{i=1}^{n} (x_i - m) \\ &= m + \frac{1}{n} \sum_{i=1}^{n} x_i - \frac{1}{n}\sum_{i=1}^{n} m \\ &= m + \bar{x} - \frac{1}{n} (nm) \\ &= \bar{x} \end{aligned}

先ほどの5人の英語の点数51，72，93，80，64の平均を，仮平均を用いて求めたいと思います．ここでは，仮平均を50とします．
\begin{aligned} \bar{x} &= 50 + \frac{(51-50) + (72 - 50) + (93 - 50) + (80 -50) + (64 -50)}{5} \\ &= 50 + \frac{1 + 22 + 43 + 30 + 14}{5} \\ &= 50 + \frac{110}{5} \\ &= 50 + 22 \\ &= 72 \end{aligned}
先ほどより小さな数字の計算で済むようになりました．

分散・標準偏差

データが平均から「どれだけ散らばっているか」を示す指標に分散があります．

分散の定義．
n個のデータx_1, x_2, \cdots , x_nの平均 \bar{x}とすると，分散s_{x}は，
\begin{aligned} s_{x} &= \frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{n} \\ &= \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \end{aligned}

(x_1 - \bar{x})をx_1の平均からの偏差といいます．

また，分散の正の平方根\sqrt{s_{x}}のことを標準偏差といいます．

以下の記事の再掲となりますが，分散に関する性質をひとつ紹介したいと思います．

総和Σと総乗Π

命題．
n個のデータx_1, x_2 , \cdots x_nの平均を\overline{x}，分散をs^2，n個のデータの2乗の平均を\overline{x^2}とするとき，以下の等式が成り立つ．
s^2 = \overline{x^2} - \left( \overline{x} \right)^2

証明．
\begin{aligned} s^2 &= \frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2 \\ &= \frac{1}{n} \left\{ \sum_{i=1}^n x_i^2 -2 \sum_{i=1}^n \overline{x} x_i + \sum_{i=1}^n (\overline{x})^2 \right\} \\ &= \frac{1}{n} \sum_{i=1}^n x_i^2 - 2\overline{x} \frac{1}{n} \sum_{i=1}^n x_i + \frac{1}{n} n(\overline{x})^2 \\ &= \overline{x^2} -2\left( \overline{x} \right)^2 + \left( \overline{x} \right)^2 \\ &= \overline{x^2} -\left( \overline{x} \right)^2 \end{aligned}

共分散

共分散の定義．
2つの変量xとyのデータの組がn個あり，それを(x_1, y_1), (x_2, y_2), \cdots , (x_n, y_n)とすると，共分散s_{xy}は，
\begin{aligned} s_{xy} &= \frac{(x_1 - \bar{x})(y_1 - \bar{y}) + (x_2 - \bar{x})(y_2 - \bar{y}) + \cdots + (x_n - \bar{x})(y_n - \bar{y})}{n} \\ &= \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \end{aligned}

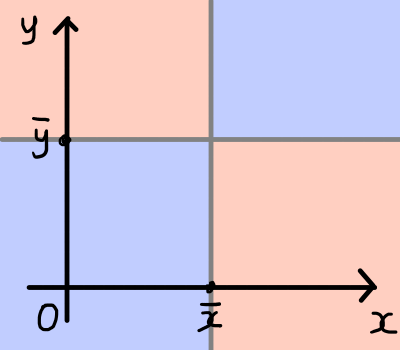
(x_i - \bar{x})(y_i - \bar{y})の値とデータの関係を下の図を使って説明しますと，(x_i - \bar{x})(y_i - \bar{y})> 0のときデータの組(x_i , y_i)は青い領域にあり，(x_i - \bar{x})(y_i - \bar{y})< 0のとき(x_i , y_i)は赤い領域にあります．

命題．
2つの変量xとyのデータの組がn個あり，それを(x_1, y_1), (x_2, y_2), \cdots , (x_n, y_n)とする．さらに，xとyの平均値をそれぞれ\bar{x}と\bar{y}とすると，以下の式が成り立つ．
\begin{aligned} s_{xy} &= \frac{1}{n} \left( \sum_{i=1}^{n} x_i y_i \right) - \bar{x} \cdot \bar{y} \\ \end{aligned}

証明．
\begin{aligned} s_{xy} &= \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \\ &= \frac{1}{n} \sum_{i=1}^{n} (x_i y_i - x_i \bar{y} - y_i \bar{x} + \bar{x} \cdot \bar{y}) \\ &= \frac{1}{n} \sum_{i=1}^{n} x_i y_i - \frac{1}{n} \sum_{i=1}^{n} x_i \bar{y} - \frac{1}{n} \sum_{i=1}^{n} y_i \bar{x} + \frac{1}{n} \sum_{i=1}^{n} \bar{x} \cdot \bar{y} \\ &= \frac{1}{n} \sum_{i=1}^{n} x_i y_i - \frac{1}{n} \bar{y} \sum_{i=1}^{n} x_i - \frac{1}{n} \bar{x} \sum_{i=1}^{n} y_i + \frac{1}{n} n \bar{x} \cdot \bar{y} \\ &= \frac{1}{n} \left( \sum_{i=1}^{n} x_i y_i \right) - \bar{x} \cdot \bar{y} - \bar{x} \cdot \bar{y} + \bar{x} \cdot \bar{y} \\ &= \frac{1}{n} \left( \sum_{i=1}^{n} x_i y_i \right) - \bar{x} \cdot \bar{y} \end{aligned}

さらに
\begin{aligned} \frac{1}{n} \left( \sum_{i=1}^{n} x_i y_i \right) = \bar{xy} \end{aligned} とおくと，
\begin{aligned} s_{xy} &= \bar{xy} - \bar{x} \cdot \bar{y} \end{aligned}
と表すこともできます．

相関係数

定義．
2つの変量xとyのデータの組がn個あり，それを(x_1, y_1), (x_2, y_2), \cdots , (x_n, y_n)とする．さらに，xとyの分散をそれぞれs_xとs_yとし，共分散をs_{xy}とすると，相関係数rは，
\begin{aligned} r &= \frac{s_{xy}}{\sqrt{s_x} \sqrt{s_y}} \end{aligned}

相関係数rのとりうる範囲は-1 \leqq r \leqq 1であり，0に近いほど無相関，1に近いほど正の相関，-1に近いほど負の相関があります．

　　

「勝手気ままに高校数学」シリーズ一覧へ