ハフマン符号について
データの圧縮方法には,データを元通りに復元可能な可逆圧縮と,元通りに戻せない非可逆圧縮が存在します.そして,可逆圧縮の代表例のひとつがハフマン符号1教科書によってはハフマン法ともです.
本記事では,ハフマン符号による文字列の圧縮について解説します.
目次
ハフマン符号化の手順
ハフマン符号化の大まかな手順は以下のようになります.
- 文字の出現回数を数える
- ハフマン木の作成
- ハフマン木に「0」と「1」の割り振り
- 文字とビット列(符号)の対応に合わせて符号化
これから符号化の手順を見ていくのですが,実際の文字列を扱う方が分かりやすいため,ここでは「aaaabbbccde」という文字列を符号化することを考えます.
比較対象として以下のような愚直な符号化を考えてみましょう.
| 文字 | 符号(ビット列) |
| a | 000 |
| b | 001 |
| c | 010 |
| d | 011 |
| e | 100 |
このように符号を割り当てると,文字列「aaaabbbccde」は「000000000000001001001010010011100」と33ビットで表すことができます.
ハフマン符号化では,これよりも必要なビット数が少なくなります.ハフマン符号化の考え方はシンプルで,出現頻度の高い文字には短いビット列を,出現頻度の低い文字列には長い文字列を割り当てます.
それでは,「aaaabbbccde」をハフマン符号化してみましょう.
手順1.文字の出現回数を数える
文字列「aaaabbbccde」の文字の出現回数は以下のようになります.
| 文字 | 出現回数 |
| a | 4 |
| b | 3 |
| c | 2 |
| d | 1 |
| e | 1 |
手順2.ハフマン木の作成
ハフマン符号化では,ハフマン木という特殊な木構造2できるだけ木構造の用語を知らなくてもよい解説にします.を作ります.ハフマン木作成の手順を説明しながら,文字列「aaaabbbccde」のハフマン木を作りたいと思います.
手順1.文字を出現回数の多い順に並べ,文字の上に出現回数を書いておきます.
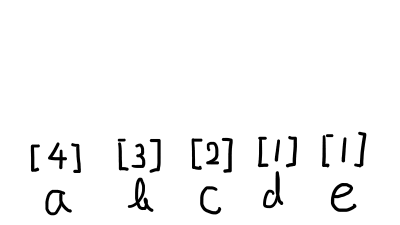
手順2.出現回数が最も小さい2つを下の図のように結び合わせて,その上に出現回数の和を書きます.結び合わせた数字(今回の場合は[1][1])は,今後の比較から外します.
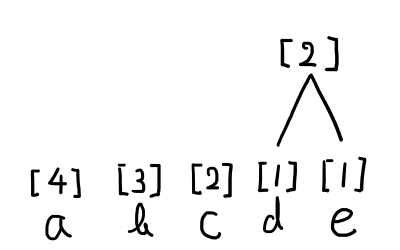
手順3.残った数字(結び合わせた数字を含む)の中から,最も小さい2つを結び合わせて,その上に出現回数の和を書きます.結び合わせた数字(今回の場合は[2][2])は,今後の比較から外します.この操作を,数字がひとつになるまで続けます.

補足.最も小さい数字が3つ以上ある場合は,どれを組み合わせても構いません.同様に,2番目に小さい数字が2つ以上ある場合は,どれを2番目の数字として選択しても構いません.上の図の次の手順を考えると,1番小さい数字は[3]で確定していますが,2番目に小さい[4]が2つあります.ここでは下の図のように,右の[4]と結合させました.
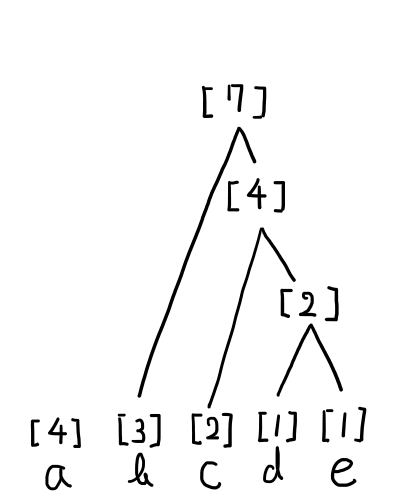
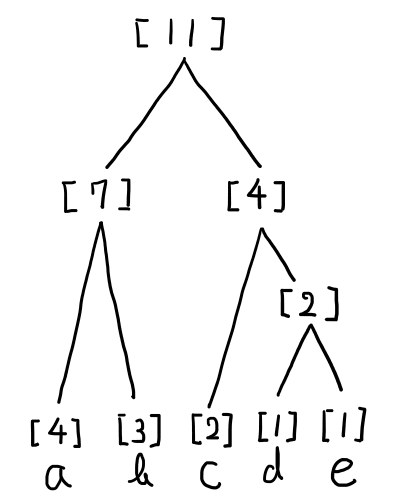
最後まで終わらせると,以下のような図になります.
このような図のことをハフマン木といいます.
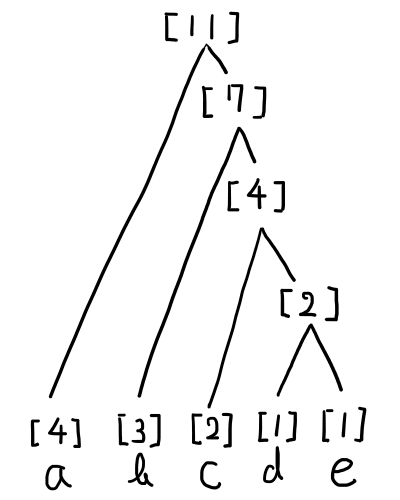
これでハフマン木が完成しました!
ちなみに,2つの[3]からひとつを選ぶところで,左の[3]を選ぶと以下のようなハフマン木になります.
手順3.ハフマン木に「0」と「1」の割り振り
ハフマン木の数字と数字の間に「0」か「1」を割り振ります.枝分かれするところに「0」「1」を割り振るイメージです.
左に枝分かれすれば「0」,右だと「1」を割り振ってみましょう.すると以下のような,割り当てになります.
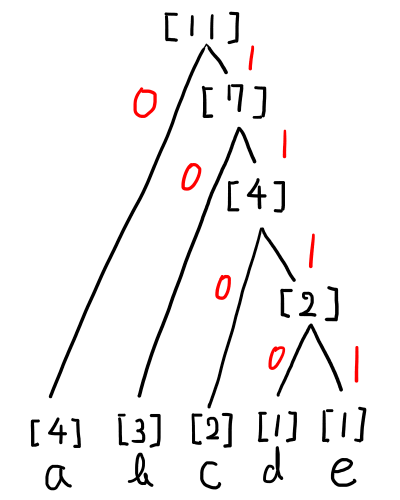
左が「1」,右が「0」だと以下のようになります.
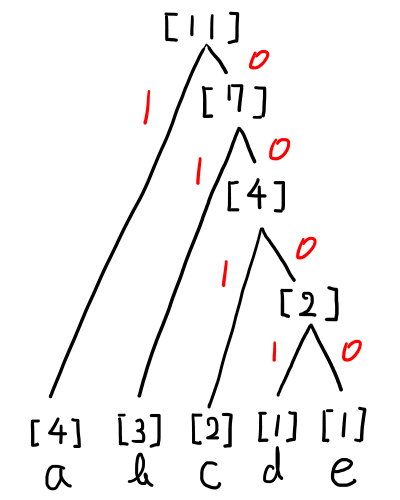
ちなみに,もうひとつのハフマン木の割り当ては以下のような形になります.
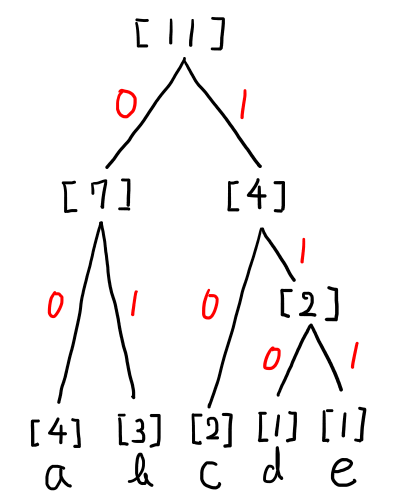
もうひとつ.
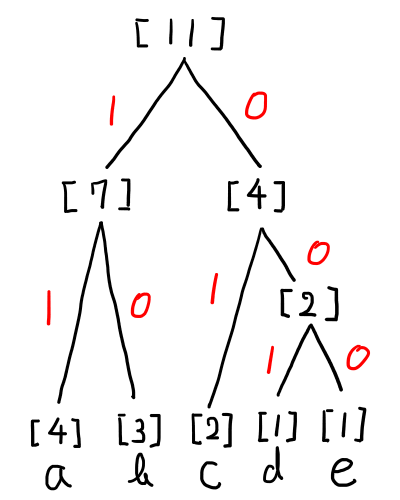
ちなみにここまでを見て,4種類の符号化のパターンが出来そうだと気づいた方もいると思いますが,その通りで今回の文字列の場合,この4種類は全て正しいハフマン木で,符号化のパターンも4種類あります.
手順4.文字とビット列(符号)の対応に合わせて符号化
文字とビット列(符号)の対応表を作り,文字列「aaaabbbccde」を符号化します.
文字に対応する符号を求めるために,ハフマン木の一番上の数字(根)から目的の文字までをたどります.たどったときに現れる「0」「1」を順番に繋げると,対応する符号になります.
以下の図のハフマン木の場合,「b」の符号は「10」です.下の図のように,一番上から「b」までをたどったときに現れる「1」と「0」を順番に合わせることで求められます.
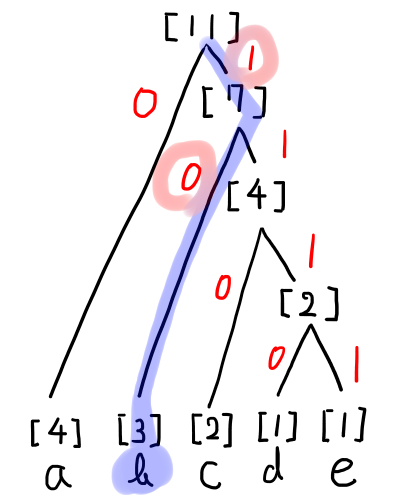
上の図のハフマン木の場合,文字と符号の対応表は以下のようになります.
| 文字 | 符号(ビット列) |
| a | 0 |
| b | 10 |
| c | 110 |
| d | 1110 |
| e | 1111 |
また「aaaabbbccde」を符号化すると「000010101011011011101111」となります.
同様に以下のハフマン木の場合は,

| 文字 | 符号(ビット列) |
| a | 1 |
| b | 01 |
| c | 001 |
| d | 0001 |
| e | 0000 |
「aaaabbbccde」の符号化は「111101010100100100010000」です.
以下のハフマン木の場合は,

| 文字 | 符号(ビット列) |
| a | 00 |
| b | 01 |
| c | 10 |
| d | 110 |
| e | 111 |
「aaaabbbccde」の符号化は「000000000101011010110111」です.
以下のハフマン木の場合は,

| 文字 | 符号(ビット列) |
| a | 11 |
| b | 10 |
| c | 01 |
| d | 001 |
| e | 000 |
「aaaabbbccde」の符号化は「111111111010100101001000」です.
「aaaabbbccde」をハフマン符号化すると,
「000010101011011011101111」
「111101010100100100010000」
「000000000101011010110111」
「111111111010100101001000」
のいずれかになります.いずれの場合も24ビットになります.記事の初めに試した方法では33ビットでしたので,あの手法よりも9ビット短く符号化できました.
データの復号
ハフマン符号化は可逆圧縮です.
復号(デコード)をすることで,本当に可逆圧縮なのか確かめてみましょう.
ここでは次の対応表を使って,ビット列「000010101011011011101111」を復号します.
| 文字 | 符号(ビット列) |
| a | 0 |
| b | 10 |
| c | 110 |
| d | 1110 |
| e | 1111 |
「0」から始まるものは「a」だけなので,最初の「0000」は「aaaa」であることが分かります.
次の数字は「1」ですが,「1」から始まるものはたくさんあるため,まだ特定はできません.「1」の次が「0」なのでここで,「10」の部分が「b」であると分かります.同様に続けていくと,「aaaabbbccde」と復号することができます.
何気なく復号しましたが,ここにはハフマン符号化の重要な性質が隠れています.それは,「頭から順に1度見ただけで復号できる」という性質です.この性質のおかげで,データを何度も読み込むことなく復号することができます.
今回は「aaaabbbccde」という分かりやすい文字列でしたので,信じられない方もいるかもしれません.そこで「a」4つ「b」3つ「c」2つ「d」1つ「e」1つの文字列を適当に作り,符号化と復号をしてみてください.頭から順に1度見ただけで復号できます.
この性質について詳しく知りたい人には,こちらのWikipediaのページをオススメします.
練習問題
- 「a」4つ「b」3つ「c」2つ「d」1つ「e」1つの文字列を適当に作り,符号化と復号をしましょう.
- 文字列「huffman coding is lossless compression」をハフマン符号を使って符号化しましょう.ただしスペース「 」を文字として認識するものとします.無駄な手間を減らすために,文字の出現回数の表を以下に用意しました.
| 文字 | 出現回数 |
| a | 1 |
| c | 2 |
| d | 1 |
| e | 2 |
| f | 2 |
| g | 1 |
| h | 1 |
| i | 3 |
| l | 2 |
| m | 2 |
| n | 3 |
| o | 4 |
| p | 1 |
| r | 1 |
| s | 7 |
| u | 1 |
| _(スペース) | 4 |

