一度は証明したい三角比の公式(三角形の面積,四角形の面積)
この記事では,三角形や四角形の面積を求める公式の証明を行います.
証明をしたことがない公式を見つけたら,記事を読み終わった後で良いので,自分で証明してみましょう.
また本記事では,三角形\bigtriangleup ABCに関して,\angle AをA,\angle BをB,\angle CをCと記述します.辺については\angle Aの対辺をa,\angle Bの対辺をb,\angle Cの対辺をcと記述とします.
三角形の面積の公式
三角形の面積を求める公式(底辺) \times (高さ) \div 2を三角比を使って少し変形します.
三角形\bigtriangleup ABCの面積Sについて,以下の式が成り立つ.
\begin{aligned}
S &= \frac{1}{2} bc \sin{A}
\end{aligned}
\bigtriangleup ABCの頂点Cから辺ABへの垂線と直線ABとの交点をDとする.CDの長さは,
\begin{aligned}
\sin A &= \frac{CD}{b} より\\
CD &= b \sin A
\end{aligned}
よって\bigtriangleup ABCの面積Sは,
\begin{aligned}
S &= \frac{1}{2} \cdot c \cdot b \sin A \\
&= \frac{1}{2}bc \sin{A}
\end{aligned}
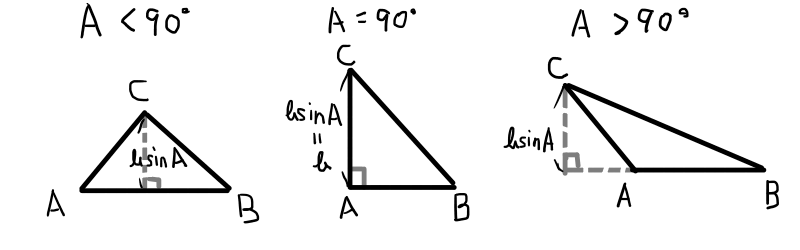
同様の方法で,
\begin{aligned}
S &= \frac{1}{2} ca \sin{B}
\end{aligned}
\begin{aligned}
S &= \frac{1}{2} ab \sin{C}
\end{aligned}
を求めることができます.
三角形の面積と外接円の関係
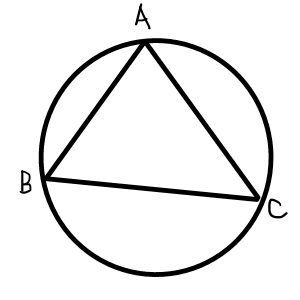
三角形\bigtriangleup ABCの面積Sと外接円の半径Rに関して,以下の等式が成り立ちます.
\begin{aligned} S &= \frac{abc}{4R} \end{aligned}
三角形\bigtriangleup ABCの外接円の半径をRとする.
正弦定理\frac{a}{\sin A} = 2Rより,
\sin A = \frac{a}{2R}
\bigtriangleup ABCの面積Sは,
\begin{aligned}
S &= \frac{1}{2}bc \sin{A} \\
&= \frac{abc}{4R}
\end{aligned}
三角形の面積と内接円の関係
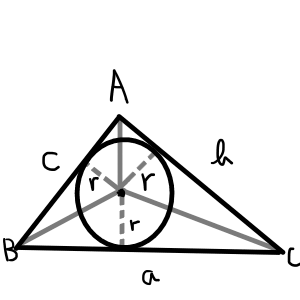
三角形\bigtriangleup ABCの面積Sと内接円の半径rに関して,以下の等式が成り立ちます.
S = \frac{1}{2} r \left( a + b + c \right)
証明.
\begin{aligned}
S &= \frac{1}{2} a r + \frac{1}{2} b r + \frac{1}{2} c r \\
&= \frac{1}{2}r \left( a + b + c \right)
\end{aligned}
ヘロンの公式
三角形の各辺の長さから,面積を求める公式にヘロンの公式と呼ばれるものがあります.
ヘロンの公式
三角形\bigtriangleup ABCの面積S,s = \frac{a +b + c}{2}とすると,
S = \sqrt{s(s-a)(s-b)(s-c)}
証明.
\begin{aligned}
S &= \frac{1}{2}bc \sin{A} \\
&= \frac{1}{2}bc \sqrt{1 - \cos^2 A} \\
&= \frac{1}{2}bc \sqrt{\left(1 + \cos A \right) \left(1 - \cos A \right) }
\end{aligned}
ここで余弦定理より,
\begin{aligned}
a^2 &= b^2 + c^2 -2bc \cos A \\
2bc \cos{A} &= b^2 + c^2 - a^2 \\
2bc + 2bc \cos A &= 2bc + b^2 + c^2 - a^2 \\
2bc \left( 1 + \cos A \right) &= (b+c)^2 - a^2 \\
1 + \cos A &= \frac{\left( b + c + a \right) \left( b + c - a \right) }{2bc}
\end{aligned}
ここで,s = \frac{a +b + c}{2}とおくと,
\begin{aligned}
1 + \cos A &= \frac{\left( b + c + a \right) \left( b + c - a \right) }{2bc} \\
&= \frac{2s \left( 2s - 2a \right) }{2bc} \\
&= 2 \frac{s \left( s - a \right) }{bc} \\
\end{aligned}
同様に,余弦定理より
\begin{aligned}
a^2 &= b^2 + c^2 -2bc \cos A \\
-2bc \cos{A} &= a^2 - b^2 - c^2 \\
2bc - 2bc \cos A &= 2bc + a^2 - b^2 - c^2 \\
2bc \left( 1 - \cos A \right) &= a^2 - (b-c)^2 \\
1 - \cos A &= \frac{\left( a + b - c \right) \left( a - b + c \right) }{2bc}
\end{aligned}
ここで,s = \frac{a +b + c}{2}とおくと,
\begin{aligned}
1 - \cos A &= \frac{\left( a - b + c \right) \left( a + b - c \right) }{2bc} \\
&= \frac{\left( 2s - 2b \right) \left( 2s - 2c \right) }{2bc} \\
&= 2 \frac{\left( s - b \right) \left( s - c \right) }{bc} \\
\end{aligned}
面積の式に戻って,
\begin{aligned}
S &= \frac{1}{2}bc \sqrt{\left(1 + \cos A \right) \left(1 - \cos A \right) } \\
&= \frac{1}{2} bc \sqrt{ \left\{ 2 \frac{s \left( s - a \right) }{bc} \right\} \left\{ 2 \frac{\left( s - b \right) \left( s - c \right) }{bc} \right\} } \\
&= \sqrt{s(s-a)(s-b)(s-c)}
\end{aligned}
平行四辺形の面積の公式
平行四辺形の面積Sは,合同な三角形が2つあると考えて,2辺と間の角から,
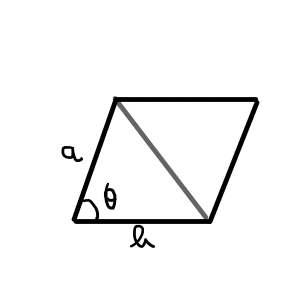
\begin{aligned} S &= ab \sin{\theta} \end{aligned}
円に内接する四角形の面積(ブラーマグプタの公式)
円に内接する四角形の面積Sを各辺の長さから求める公式があります.
以下に示す公式をブラーマグプタの公式といいます.
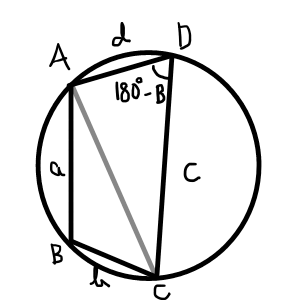
ブラーマグプタの公式
円に内接する四角形ABCDの辺ABの長さをa,辺BCの長さをb,辺CDの長さをc,辺DAの長さをd,面積をS,s = \frac{a +b + c + d}{2}とすると,
S = \sqrt{(s-a)(s-b)(s-c)(s-d)}
証明.
\begin{aligned}
S &= (三角形 \bigtriangleup ABC の面積)+(三角形 \bigtriangleup ACD の面積) \\
&= \frac{1}{2}ab \sin{B} + \frac{1}{2}cd \sin{D} \\
&= \frac{1}{2}ab \sin{B} + \frac{1}{2}cd \sin{(180^{\circ}-B)} \\
&= \frac{1}{2}ab \sin{B} + \frac{1}{2}cd \sin{B} \\
&= \frac{1}{2} (ab + cd) \sin{B} \\
&= \frac{1}{2} (ab + cd) \sqrt{1 - cos^2B} \\
&= \frac{1}{2} (ab + cd) \sqrt{(1 + cos{B})(1 - cos{B})} \\
\end{aligned}
ここで余弦定理より,
\begin{aligned}
AC^2 &= a^2 + b^2 -2ab \cos{B}
\end{aligned}
また,
\begin{aligned}
AC^2 &= c^2 + d^2 -2cd \cos{D} \\
&= c^2 + d^2 -2cd \cos{(180^{\circ} - B)} \\
&= c^2 + d^2 + 2cd \cos{B} \\
\end{aligned}
上の2つの式から,
\begin{aligned}
a^2 + b^2 -2ab \cos{B} &= c^2 + d^2 + 2cd \cos{B} \\
2(ab+cd) \cos{B} &= a^2 + b^2 - c^2 - d^2 \\
\cos{B} &= \frac{a^2 + b^2 - c^2 - d^2}{2(ab+cd)}
\end{aligned}
\begin{aligned}
1 + \cos{B} &= 1 + \frac{a^2 + b^2 - c^2 - d^2}{2(ab+cd)} \\
&= \frac{2ab + 2cd + a^2 + b^2 - c^2 - d^2}{2(ab+cd)} \\
&= \frac{(a + b)^2 - (c - d)^2}{2(ab+cd)} \\
&= \frac{(a + b + c - d)(a + b - c + d)}{2(ab+cd)} \\
\end{aligned}
ここで,s = \frac{a +b + c + d}{2}とおいて,
\begin{aligned}
1 + \cos{B} &= \frac{(a + b + c - d)(a + b - c + d)}{2(ab+cd)} \\
&= \frac{(2s -2d)(2s-2c)}{2(ab+cd)} \\
&= 2 \frac{(s-c)(s-d)}{ab+cd}
\end{aligned}
\begin{aligned}
1 - \cos{B} &= 1 - \frac{a^2 + b^2 - c^2 - d^2}{2(ab+cd)} \\
&= \frac{2ab + 2cd - a^2 - b^2 + c^2 + d^2}{2(ab+cd)} \\
&= \frac{(c + d)^2 - (a - b)^2}{2(ab+cd)} \\
&= \frac{(c + d + a - b)(c + d - a + b)}{2(ab+cd)} \\
\end{aligned}
ここで,s = \frac{a +b + c + d}{2}とおいて,
\begin{aligned}
1 - \cos{B} &= \frac{(c + d + a - b)(c + d - a + b)}{2(ab+cd)} \\
&= \frac{(2s -2b)(2s-2a)}{2(ab+cd)} \\
&= 2 \frac{(s-a)(s-b)}{ab+cd}
\end{aligned}
面積の式に戻って,
\begin{aligned}
S &= \frac{1}{2} (ab + cd) \sqrt{(1 + cos{B})(1 - cos{B})} \\
&= \frac{1}{2} (ab + cd) \sqrt{ \left\{ 2 \frac{(s-c)(s-d)}{ab+cd} \cdot 2 \frac{(s-a)(s-b)}{ab+cd} \right\} } \\
&= \sqrt{(s-a)(s-b)(s-c)(s-d)}
\end{aligned}
