三角形の五心　〜性質と証明〜

本記事では，三角形の五心について解説を行います．
ここで書かれる命題の証明は，証明方法のほんの一例にすぎませんので，ぜひ自分なりの証明に挑戦してみてください．
また，中学校で習う定理・命題に関しましては，図を省略していることがあります．分かりにくい場合は，ぜひ自分で図を描いてみてください．

外心

外心の押さえておきたいポイントは以下の3点です．

• 三角形の外接円の中心である．
• 三角形の3つの辺の垂直二等分線は1点(外心)で交わる．
• 外心から各頂点までの距離は等しい．

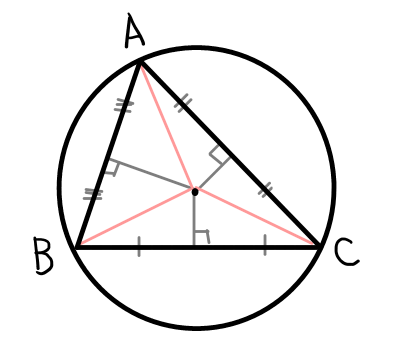
下の図のように外心が三角形の外にある場合もあります．

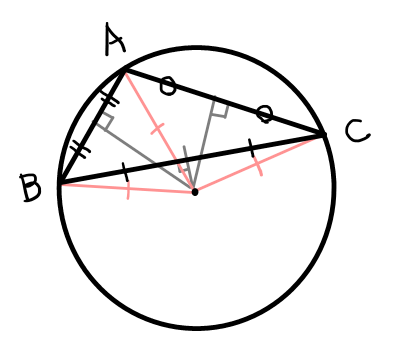
それでは先ほど書いた3つのポイントは一度忘れて，それぞれの性質が成り立つか確かめてみましょう．

重要な定理を証明するために，まずは垂直二等分線に関する以下の命題を証明します．

命題．
線分\mathrm{AB}と点\mathrm{P}が存在するとき，点\mathrm{P}が線分\mathrm{AB}の垂直二等分線上にあるならば，\mathrm{AP} = \mathrm{BP}が成り立つ．

証明．
線分\mathrm{AB}の中点を\mathrm{M}とする．
線分\mathrm{PM}は共通しており，中点なので\mathrm{AM} = \mathrm{BM}，\angle \mathrm{PMA} = \angle \mathrm{PMB}より，2辺と間の角が等しいので，
\bigtriangleup \mathrm{AMP} \equiv \bigtriangleup \mathrm{BMP}
よって，
\mathrm{AP} = \mathrm{BP}

先ほどの命題の逆も成り立ちます．

命題．
線分\mathrm{AB}と点\mathrm{P}が存在するとき，\mathrm{AP} = \mathrm{BP}が成り立つならば，点\mathrm{P}が線分\mathrm{AB}の垂直二等分線上にある．

証明．
線分\mathrm{AB}の中点を\mathrm{M}とする．
\mathrm{P} = \mathrm{M}ならば，\mathrm{P}は垂直二等分線上の点である．
\mathrm{P} \neq \mathrm{M}の場合，
\mathrm{AP} = \mathrm{BP}，\mathrm{AM} = \mathrm{BM}，\mathrm{PM}は共通より，3辺が等しいため，
\bigtriangleup \mathrm{AMP} \equiv \bigtriangleup \mathrm{BMP}
となる．よって\angle \mathrm{AMP} = \angle \mathrm{BMP}かつ，\angle \mathrm{AMP} + \angle \mathrm{BMP} = 180^{\circ}より，\angle \mathrm{AMP} = \angle \mathrm{BMP}=90^{\circ}
つまり
\mathrm{AB} \perp \mathrm{PM}
したがって，点\mathrm{P}は垂直二等分線上の点である．

それでは，外心に関わる命題を証明していきましょう．

定理．¹命題の中でも特に重要なものを「定理」と呼びます．
三角形の3辺の垂直二等分線は1点で交わる．

証明．
\bigtriangleup \mathrm{ABC}の辺\mathrm{AB}と辺\mathrm{BC}の垂直二等分線の交点を\mathrm{O}とする．辺\mathrm{AB}の中点を\mathrm{M}，辺\mathrm{BC}の中点を\mathrm{M}^{\prime}とすると，
\bigtriangleup \mathrm{AMO} \equiv \bigtriangleup \mathrm{BMO}
\bigtriangleup \mathrm{BM^{\prime}O} \equiv \bigtriangleup \mathrm{CM^{\prime}O}
よって，
\mathrm{OA} = \mathrm{OB}
\mathrm{OB} = \mathrm{OC}
が成り立つ．したがって，
\mathrm{OA} = \mathrm{OC}
も成り立つ．よって，\mathrm{O}は辺\mathrm{CA}の垂直二等分線上にあり，3辺の垂直二等分線が1点で交わることが示された．

ちなみに\mathrm{OA} = \mathrm{OB} = \mathrm{OC}より，\mathrm{O}を中心とした\bigtriangleup \mathrm{ABC}の外接円が存在することが分かります．

内心

内心の押さえておきたいポイントは以下の3点です．

• 三角形の内接円の中心である．
• 三角形の3つの内角の二等分線は1点(内心)で交わる．
• 内心から各辺までの距離は等しい．

外心のときと同様に，先ほど書いた3つのポイントは一度忘れて，それぞれの性質が成り立つか確かめてみましょう．

まずは外心のときと同様に，重要な定理につながる命題を証明します．

命題．
同一平面上に半直線\mathrm{OA}と\mathrm{OB}が存在するとき，\angle \mathrm{AOB}の二等分線上の点\mathrm{P}から半直線\mathrm{OA}，\mathrm{OB}への距離は等しい．

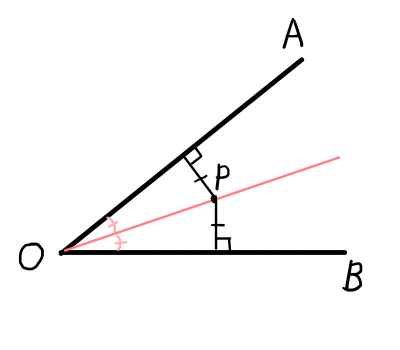
証明．
半直線\mathrm{OA}と点\mathrm{P}から\mathrm{OA}への垂線との交点を点\mathrm{D}，同様に，半直線\mathrm{OB}と点\mathrm{P}から\mathrm{OB}への垂線との交点を点\mathrm{E}とする．
点\mathrm{P}は\angle \mathrm{AOB}の二等分線上にあるため，
\angle \mathrm{DOP} = \angle \mathrm{EOP}
また，辺\mathrm{OP}は共有しており，\angle \mathrm{ODP} = \angle \mathrm{OEP} = 90^{\circ}なので，
\bigtriangleup \mathrm{OPD} \equiv \bigtriangleup \mathrm{OPE}
よって，
\mathrm{PD} = \mathrm{PE}

少しだけ条件を追加すれば，その逆も成り立ちます．

命題．
\angle \mathrm{AOB}の内側に点\mathrm{P}があり，半直線\mathrm{OA}，\mathrm{OB}との距離が等しいとき，点\mathrm{P}は\angle \mathrm{AOB}の二等分線上に存在する．

証明．
半直線\mathrm{OA}と点\mathrm{P}から\mathrm{OA}への垂線との交点を点\mathrm{D}，同様に，半直線\mathrm{OB}と点\mathrm{P}から\mathrm{OB}への垂線との交点を点\mathrm{E}とする．
\bigtriangleup \mathrm{OPD} と \bigtriangleup \mathrm{OPE}において，三平方の定理より，
\mathrm{OD}^2 = \mathrm{OP}^2 - \mathrm{PD}^2
\mathrm{OE}^2 = \mathrm{OP}^2 - \mathrm{PE}^2
前提条件より\mathrm{PD} = \mathrm{PE}なので，
\mathrm{OD} = \mathrm{OE}
対応する3辺が等しいので，
\bigtriangleup \mathrm{OPD} \equiv \bigtriangleup \mathrm{OPE}
よって，
\angle \mathrm{POD} = \angle \mathrm{POE}
したがって，点\mathrm{P}は\angle \mathrm{AOB}の二等分線上に存在する．

定理．
\bigtriangleup \mathrm{ABC}の3つの角の二等分線は１点で交わる．

証明．
\bigtriangleup \mathrm{ABC}の\angle \mathrm{B}の二等分線と\angle \mathrm{C}の二等分線の交点を \mathrm{I}とする．\mathrm{I}から各辺へ垂線をおろし，辺\mathrm{AB}との交点を\mathrm{D}，辺\mathrm{BC}との交点を\mathrm{E}，辺\mathrm{AC}との交点を\mathrm{F}とする．
\bigtriangleup \mathrm{BDI} \equiv \bigtriangleup \mathrm{BEI}，
\bigtriangleup \mathrm{CEI} \equiv \bigtriangleup \mathrm{CFI}
よって，
\mathrm{ID} = \mathrm{IE} = \mathrm{IF}
したがって，\angle \mathrm{A}の二等分線も点\mathrm{I}を通り，3つの角の二等分線は1点で交わる．

さらに，中心が\mathrm{I} で3点\mathrm{D}，\mathrm{E}，\mathrm{F}で接する\bigtriangleup \mathrm{ABC}の内接円が存在することが分かります．

この定理はチェバの定理の逆を使った証明もできます．チェバの定理の逆についてはこちらの記事をご覧ください．

チェバの定理・メネラウスの定理

重心

重心の押さえておきたいポイントは以下の2点です．

• 三角形の3つの中線は1点(重心)で交わる．
• 重心は各中線を2:1に内分する．

三角形の各頂点と対辺の中点を結ぶ線を中線といいます．

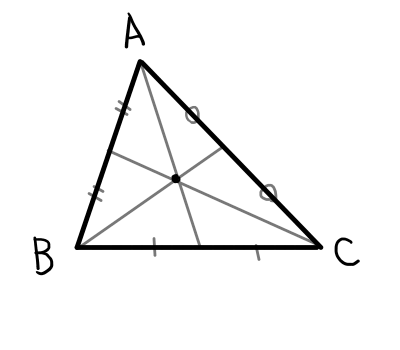
これからの証明で中点連結定理を使うので，簡単におさらいしたいと思います．

中点連結定理
\bigtriangleup \mathrm{ABC}において，辺 \mathrm{AB}の中点を \mathrm{M}，辺 \mathrm{AC}の中点を \mathrm{N}とすると，以下の2つが成り立つ．
\mathrm{BC} /\!/ \mathrm{MN}
\mathrm{BC} = 2\mathrm{MN}

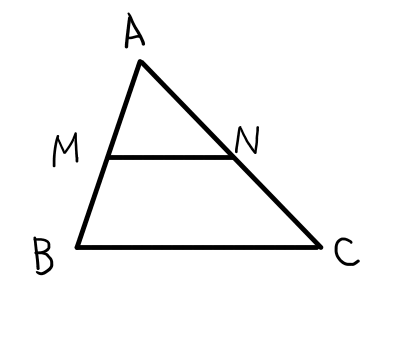
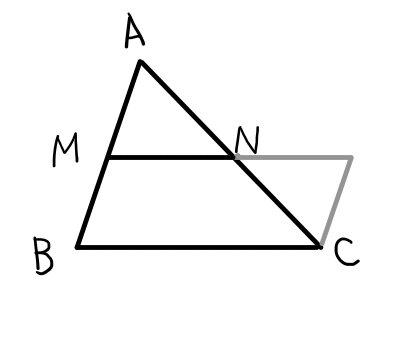
相似を使うと楽に証明ができそうですが，論理の堂々巡りを避けるために，平行四辺形と合同を利用して証明するのが筋の良いやり方です．中学校で学習済みだと思いますので，証明は省略します²下の図を見れば証明方法も分かると思います．．

まずは，2つの中線の交点が中線を2:1に内分することを示します．

定理．
\bigtriangleup \mathrm{ABC}の中線の交点は，中線を2:1に内分する．

証明．
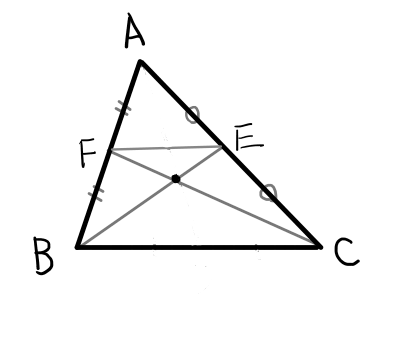
辺 \mathrm{AB}の中点を \mathrm{F}，辺 \mathrm{AC}の中点を \mathrm{E}とし，中線 \mathrm{BE}と中線 \mathrm{CF}の交点を \mathrm{G}とする．
中点連結定理より
\mathrm{BC} /\!/ \mathrm{EF}
\mathrm{BC} = 2\mathrm{EF}
このことから，\bigtriangleup \mathrm{BCG} \text{∽} \bigtriangleup \mathrm{EFG}であり，相似比は2 : 1である．よって，
\mathrm{CG} : \mathrm{FG} = \mathrm{BG} : \mathrm{EG} = 2 : 1

次に三角形の3つの中線が1点で交わることを証明します．

定理．
\bigtriangleup \mathrm{ABC}の3つの中線は１点で交わる．

証明．
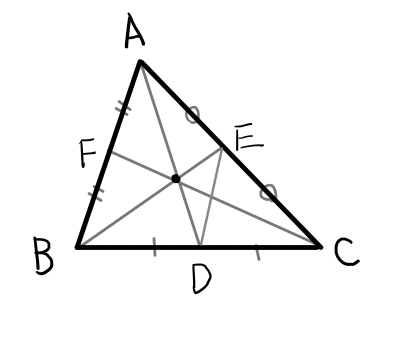
辺 \mathrm{AB}の中点を \mathrm{F}，辺 \mathrm{AC}の中点を \mathrm{E}，辺 \mathrm{BC}の中点を \mathrm{D}とし，中線 \mathrm{BE}と中線 \mathrm{CF}の交点を \mathrm{G}，中線 \mathrm{AD}と中線 \mathrm{BE}の交点を \mathrm{G^{\prime}}とする．
中点連結定理より
\bigtriangleup \mathrm{ABG^{\prime}} \text{∽} \bigtriangleup \mathrm{DEG^{\prime}}であり，相似比は2 : 1である．よって，
\mathrm{BG^{\prime}} : \mathrm{EG^{\prime}} = 2 : 1
前の定理の証明より，\mathrm{BG} : \mathrm{EG} = 2 : 1 でもあるため，\mathrm{G}と \mathrm{G^{\prime}}は同一の点である．よって，3つの中線は1点で交わる．

垂心

垂心の定義は以下の通りです．

各頂点から対辺への垂線は1点で交わり，その点を垂心という．

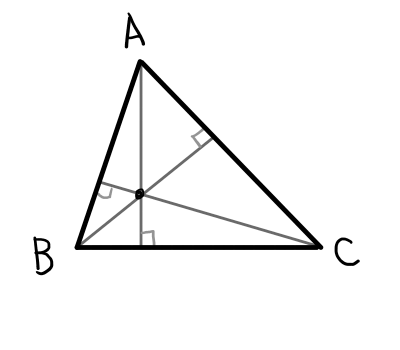
ここでは各頂点から対辺への垂線が1点で交わることを証明したいと思います．

定理．
\bigtriangleup \mathrm{ABC}の各頂点から対辺への垂線は１点で交わる．

証明．

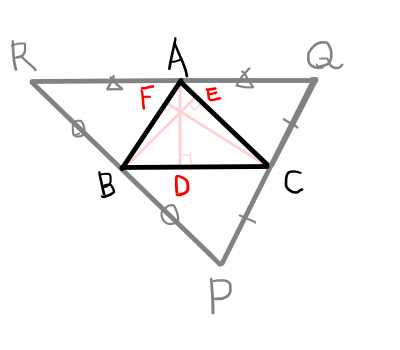
頂点 \mathrm{A}から対辺 \mathrm{BC}におろした垂線と対辺との交点を \mathrm{D}，頂点 \mathrm{B}から対辺 \mathrm{ AC}におろした垂線と対辺との交点を \mathrm{E}，頂点 \mathrm{C}から対辺 \mathrm{AB}におろした垂線と対辺との交点を \mathrm{F}とする．
また，各頂点から，対辺に平行で対辺と同じ長さの線分を頂点の両側に引き，下の図のような\bigtriangleup \mathrm{PQR}を作る．
\bigtriangleup \mathrm{ABC}の垂線は\bigtriangleup \mathrm{PQR}の垂直二等分線となるため，その交点は\bigtriangleup \mathrm{PQR}の外心となる．よって3本の垂線は1点で交わる．

他にも，外接円を持つ四角形を利用する証明方法などがあります．

傍心

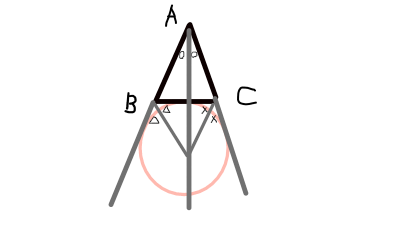
• 1つの頂点の内角の二等分線と，他の2つの頂点の外角の二等分線は1点で交わる．この点を傍心という．
• 傍心は3つある．
• 傍心を中心とし，対辺と接し，他の2辺を延長した直線と接する円が描ける．この円のことを傍心円という．

図を描くと以下のようになります．少し雑な図ですみません．

最後になりますが，次の命題の証明を演習問題として残そうと思います．
ここまでの証明と流れは大きく変わりません．ここまでの内容を理解している人ならすぐに証明できるはずです．

定理．
\bigtriangleup \mathrm{ABC}において\angle \mathrm{A}の内角の二等分線と，\angle \mathrm{B}の外角の二等分線と，\angle \mathrm{C}の外角の二等分線は1点で交わる．

ヒント³傍心から対辺\mathrm{BC}，半直線\mathrm{AB}，\mathrm{AC}への垂線を引いてみましょう．そのあとは，合同な図形を利用すれば証明できます．

　　

「勝手気ままに高校数学」シリーズ一覧へ