三角比の基礎 〜はじまりは直角三角形と相似〜
数学Ⅰで最も慣れが必要なのは何かと問われたなら,「三角比」だと応えるでしょう.数学Ⅰの内容は,基本的には中学数学の内容の延長か,集合や命題のように比較的容易なものが多いと思います.その中で三角比は少し異質でしょう.始まりこそ中学数学の延長ですが,新しい概念を巧みに扱う必要があり,慣れるまでは苦労するかもしれません.今回は少し丁寧に解説しますが,教科書や参考書を読むだけでなく,様々な問題を解いて,三角比の扱いに早く慣れるようにしましょう.
直角三角形と三角比
三角比の最も基礎となる考え方は「相似」です.相似とは,一方の図形を拡大または縮小すると,もう一方の図形と合同になる関係のことです.
ふたつの相似な直角三角形 \bigtriangleup \textup{ABC}と \bigtriangleup \mathrm{A^{\prime} B^{\prime} C^{\prime}}について考えます.ここでは\angle \mathrm{ACB}と\angle \mathrm{A^{\prime}C^{\prime}B^{\prime}}が直角であるとします.ふたつの相似な三角形は,対応する角度が3つとも等しくなるのでしたね.
相似な図形は,対応する辺の長さの比が全て等しくなります.つまり,
\mathrm{AB}:\mathrm{A^{\prime}B^{\prime}} = \mathrm{BC}:\mathrm{B^{\prime}C^{\prime}} = \mathrm{CA}:\mathrm{C^{\prime}A^{\prime}}また, \bigtriangleup \textup{ABC}の各辺の比と \bigtriangleup \mathrm{A^{\prime} B^{\prime} C^{\prime}}の各辺の比が等しくなります.
\mathrm{AB} : \mathrm{BC} : \mathrm{CA} = \mathrm{A^{\prime}B^{\prime}} : \mathrm{B^{\prime}C^{\prime}} : \mathrm{C^{\prime}A^{\prime}}直角三角形は直角以外の角が一つ定まると,全ての角が決まります.\angle \mathrm{BAC} = \thetaとすると,\angle \mathrm{ABC} = 90^{\circ} - \thetaとなります.
以上のことから,直角三角形は1つの鋭角\thetaが決まると,どの2辺の長さの比も決まる,ということが言えます.
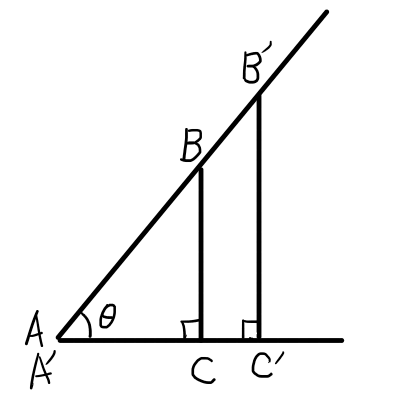
上の図のように\angle \mathrm{BAC} = \thetaとすると, \thetaの値が決まると,\frac{\mathrm{BC}}{\mathrm{AB}}と \frac{\mathrm{BC}}{\mathrm{AC}}と \frac{\mathrm{AC}}{\mathrm{BC}} が定まるというわけです.もちろん2辺の長さの比は,直角三角形の大きさによらず定まります(\frac{\mathrm{BC}}{\mathrm{AB}} = \frac{\mathrm{B^{\prime}C^{\prime}}}{\mathrm{A^{\prime}B^{\prime}}}, \frac{\mathrm{BC}}{\mathrm{AC}} = \frac{\mathrm{B^{\prime}C^{\prime}}}{\mathrm{A^{\prime}C^{\prime}}} ,\frac{\mathrm{AC}}{\mathrm{BC}} = \frac{\mathrm{A^{\prime}C^{\prime}}}{\mathrm{B^{\prime}C^{\prime}}}).
これらの2辺の長さの比をそれぞれ,\sin{\theta} (\sinはサインと読みます.),\cos{\theta} (\cosはコサイン.),\tan{\theta} (\tanはタンジェント.)といいます.
これらをもう少ししっかりと定義します.
鋭角\thetaとの位置関係から,各辺に名前をつけます.\thetaと接していない向かい側の辺のことを対辺といいます.また,直角の対辺にあたる最も長い辺を斜辺,残った辺を隣辺といいます.下の図を見るとわかりやすいでしょう.
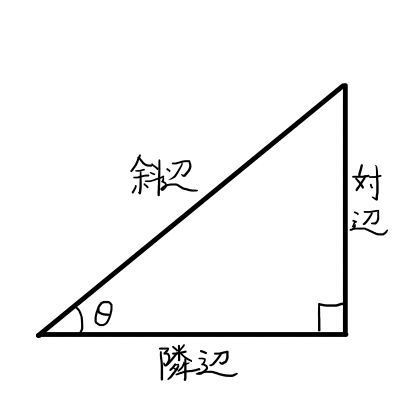
上記の通りに直角三角形の辺に名前をつけるとき,\thetaの正弦(\sin{\theta} ),余弦(\cos{\theta} ),正接(\tan{\theta} )は,以下のように表されます.
\sin{\theta} = \frac{対辺}{斜辺} \\ \\
\cos{\theta} = \frac{隣辺}{斜辺} \\ \\
\tan{\theta} = \frac{隣辺}{対辺} 覚えにくい場合は,筆記体のs,c,t(それぞれ\sin ,\cos ,\tan の頭文字)を使って,以下の図のように考えると覚えやすくなります.
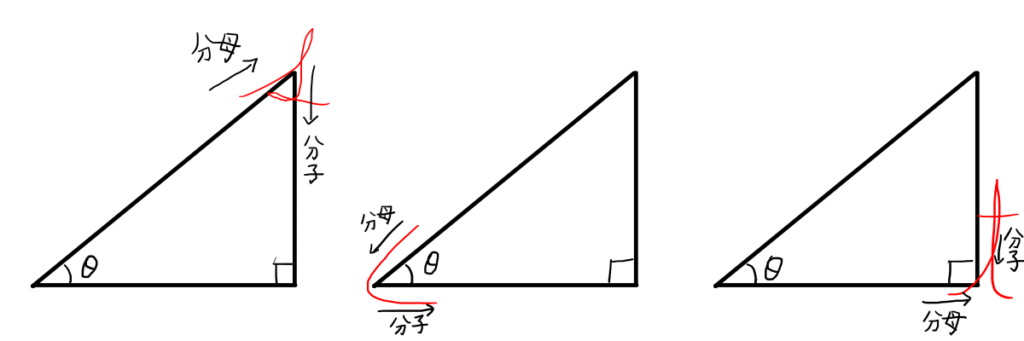
45^{\circ},30^{\circ},60^{\circ}の三角比
三角比の問題では,45^{\circ},30^{\circ},60^{\circ}がよく出てきます.これらの角度の三角比は,しっかりおさえておきたいところです.
45^{\circ}は,直角二等辺三角形の鋭角です.
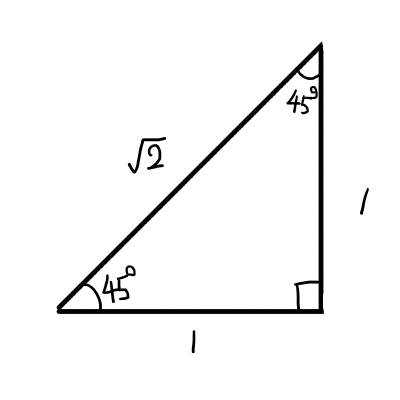
等しい長さの辺を1とすると,斜辺の長さは,三平方の定理(ピタゴラスの定理)より\sqrt{1+1} = \sqrt{2}であることがすぐに分かります.よって,正弦,余弦,正接は以下のようになります.
\sin{45^{\circ}} = \frac{1}{\sqrt{2}} \\
\\
\cos{45^{\circ}} = \frac{1}{\sqrt{2}} \\
\\
\tan{45^{\circ}} = 1 \\
次に角度が30^{\circ},60^{\circ},90^{\circ}の直角三角形を考えます.最も短い辺の長さを1とすると,下の図より,斜辺の長さは2,残った辺の長さは\sqrt{2^2 - 1^2} = \sqrt{4 - 1} = \sqrt{3}となります.
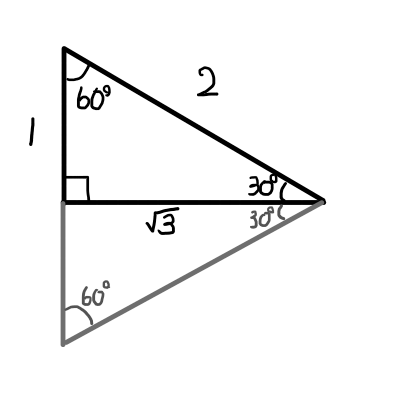
この直角三角形の30^{\circ}の角に着目すると,
\sin{30^{\circ}} = \frac{1}{2} \\
\\
\cos{30^{\circ}} = \frac{\sqrt{3}}{2} \\
\\
\tan{30^{\circ}} = \frac{1}{\sqrt{3}} \\同様に60^{\circ}の角に着目して,
\sin{60^{\circ}} = \frac{\sqrt{3}}{2} \\
\\
\cos{60^{\circ}} = \frac{1}{2} \\
\\
\tan{30^{\circ}} = \sqrt{3}\\
慣れるまでは下の図のように,着目する鋭角が左下になるように図を描き直すのもよいでしょう.
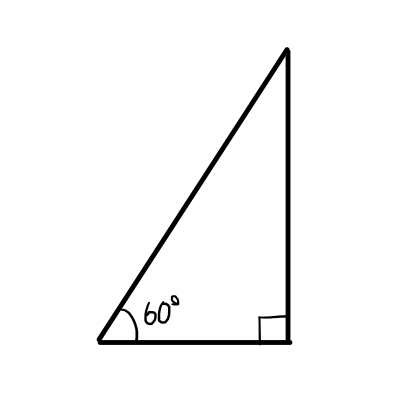
左下に着目する鋭角があれば,頭文字を使った覚え方を利用しやすくなります.

練習問題
三角比は数学Ⅰで最も中学数学と遠いものですから,まずは慣れることが重要です.
以下に簡単な練習問題を2題用意しましたが,これだけではなく,手持ちの教科書や参考書の問題を全て解き尽くすつもりで演習に励みましょう.
問題1 以下の三角形の図を見て,\sin{\theta} ,\cos{\theta} ,\tan{\theta} を求めよ.
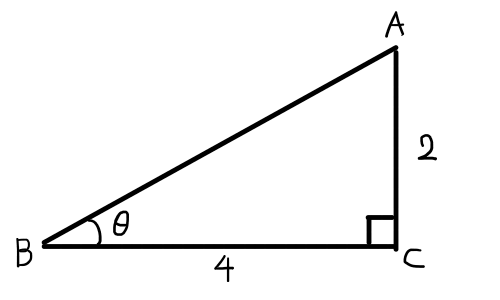
問題2 以下の三角形の図を見て,\sin{\theta} ,\cos{\theta} ,\tan{\theta} を求めよ.

練習問題の解答例
問題1の解答例
\begin{aligned}
\mathrm{AB} &= \sqrt{4^2 + 2^2} \\
&= \sqrt{20} \\
&= 2 \sqrt{5} \\
\end{aligned}
よって,\sin{\theta}= \frac{1}{\sqrt{5}} ,\cos{\theta}= \frac{2}{\sqrt{5}} ,\tan{\theta}= \frac{1}{2}
問題2の解答例
\begin{aligned}
\mathrm{AB} &= \sqrt{3^2 - (2 \sqrt{2})^2} \\
&= \sqrt{1} \\
&= 1 \\
\end{aligned}
よって,\sin{\theta}= \frac{1}{3} ,\cos{\theta}= \frac{2 \sqrt{2}}{3} ,\tan{\theta}= \frac{1}{2\sqrt{2}}
15^{\circ},75^{\circ}の三角比
本記事の最後に,15^{\circ}と75^{\circ}の三角比を求めたいと思います.
以下の図において,\angle \mathrm{BAC} = 30^{\circ},\angle \mathrm{ABC} = 60^{\circ},\angle \mathrm{ACB} = 90^{\circ},\mathrm{AB}={AD}とします.この図から,15^{\circ}と75^{\circ}を求めます.
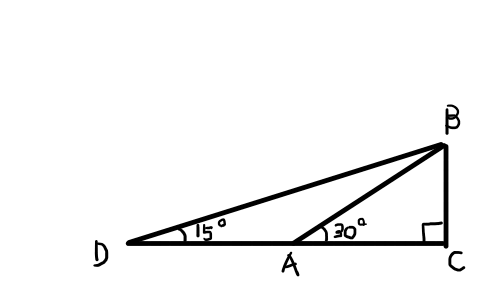
ここで,\mathrm{BC} = 1とすると,
\mathrm{AB} = \mathrm{AD} = 2,\mathrm{AC} = \sqrt{3},\mathrm{CD} = 2 +\sqrt{3}となります.
さらに,
\begin{aligned}
\mathrm{AD}^2 &= 1^2 + (2 + \sqrt{3})^2 \\
&= 1 + 7 + 4\sqrt{3} \\
&= 8 + 4 \sqrt{3} \\
\mathrm{AD} &= \sqrt{8 + 4 \sqrt{3}} \\
&= \sqrt{8 + 2 \sqrt{12}} \\
&= \sqrt{6} + \sqrt{2}
\end{aligned}
よって,
\begin{aligned}
\sin{15^{\circ}} &= \frac{1}{\sqrt{6} + \sqrt{2}} \\
&= \frac{\left(\sqrt{6} - \sqrt{2} \right)}{\left(\sqrt{6} + \sqrt{2} \right)\left(\sqrt{6} - \sqrt{2} \right)} \\
&= \frac{\sqrt{6} - \sqrt{2}}{4}
\end{aligned}
\begin{aligned}
\cos{15^{\circ}} &= \frac{2 + \sqrt{3}}{\sqrt{6} + \sqrt{2}} \\
&= \frac{\left(2 + \sqrt{3} \right) \left(\sqrt{6} - \sqrt{2} \right)}{\left(\sqrt{6} + \sqrt{2} \right)\left(\sqrt{6} - \sqrt{2} \right)} \\
&= \frac{\sqrt{6} + \sqrt{2}}{4}
\end{aligned}
\begin{aligned}
\tan{15^{\circ}} &= \frac{1}{2 + \sqrt{3}} \\
&= \frac{\left(2 - \sqrt{3} \right) }{\left(2 + \sqrt{3} \right)\left(2 - \sqrt{3} \right)} \\
&= 2 - \sqrt{3}
\end{aligned}
\begin{aligned}
\sin{75^{\circ}} &= \frac{2 + \sqrt{3}}{\sqrt{6} + \sqrt{2}} \\
&= \frac{\left(2 + \sqrt{3} \right) \left(\sqrt{6} - \sqrt{2} \right)}{\left(\sqrt{6} + \sqrt{2} \right)\left(\sqrt{6} - \sqrt{2} \right)} \\
&= \frac{\sqrt{6} + \sqrt{2}}{4}
\end{aligned}
\begin{aligned}
\cos{75^{\circ}} &= \frac{1}{\sqrt{6} + \sqrt{2}} \\
&= \frac{\left(\sqrt{6} - \sqrt{2} \right)}{\left(\sqrt{6} + \sqrt{2} \right)\left(\sqrt{6} - \sqrt{2} \right)} \\
&= \frac{\sqrt{6} - \sqrt{2}}{4}
\end{aligned}
\begin{aligned}
\tan{75^{\circ}} &= 2 + \sqrt{3}
\end{aligned}
予告
今回は直角三角形と相似から,三角比を定義しました.ひとつの鋭角が決まれば,辺の長さの比も決まるというのが重要なポイントです.
しかし直角三角形を使う手法だと,\thetaの範囲が0^{\circ} < \theta < 90^{\circ}となってしまいます.次回のテーマは,三角比の0^{\circ} \leqq \theta \leqq 180^{\circ}への拡張です.なぜ一般角まで拡張しないのか,よく分かりませんが,学習指導要領に合わせて三角比を拡張したいと思います.
↓続きの記事↓
