三角比の拡張 〜原点Oを中心とするxy平面上の円〜
この記事は,前回の記事の続きです.
前回の記事では,直角三角形を用いて鋭角(0^{\circ} < \theta < 90^{\circ})の三角比を定義しました.しかし,この方法では90^{\circ}度以上の三角比を定義できません.この記事では,三角比を0^{\circ} \leqq \theta \leqq 180^{\circ}に拡張したいと思います1本当は一般角に拡張したいのですが,学習指導要領的には数学Ⅱの範囲のようなので,中途半端に拡張します..
原点を中心とする円と三角比
xy平面上に,中心が原点で半径がrの半円を描きましょう.点\mathrm{A}の座標を(r, 0)とし,円周上の点\mathrm{P} = (x,y)を取り,\angle \mathrm{AOP} = \thetaとします.(別の捉え方として,線分\mathrm{OA}の点\mathrm{O}を固定して,角度\thetaだけ左に回転させた線分を\mathrm{OP}と考えてもよいでしょう.)\thetaが鋭角となるように\mathrm{P} を定めた場合を考えると,以下の図のようになります.
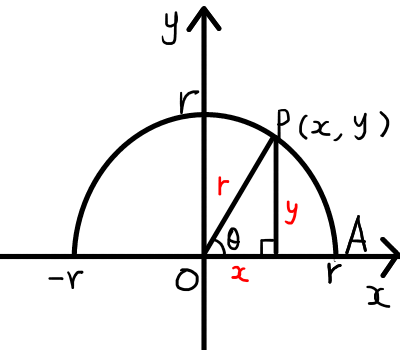
\thetaが鋭角のとき,上の図のように,各辺の長さがx,y,rの直角三角形について考えると,三角比は次のように表されます.
\sin{\theta} = \frac{y}{r} \\
\\
\cos{\theta} = \frac{x}{r} \\
\\
\tan{\theta} = \frac{y}{x} \\これを三角比の新しい定義とします.すると,0^{\circ} \leqq \theta \leqq 180^{\circ}に対して,三角比が求まります.ただし,\tan{90^{\circ}}は分母が0となるため,定義されません.
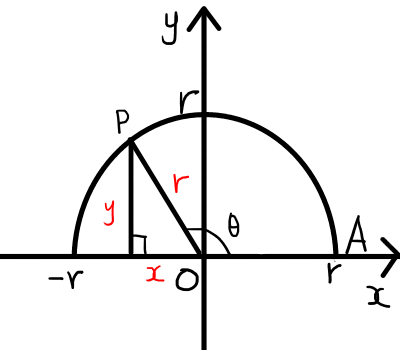
\thetaが鈍角の場合は,上の図のようになります.
ちなみに,一般角2180^{\circ}以上の角度や負の角度も含む角度の三角比も同様の定義なのですが,数学Ⅰでは0^{\circ} \leqq \theta \leqq 180^{\circ}のみを扱います.
単位円と三角比
原点を中心とする半径1の円のことを,単位円といいます.
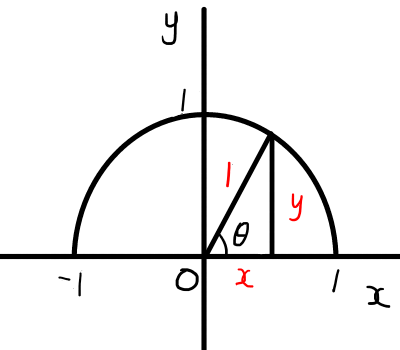
単位円で考えると,三角比がとても分かりやすくなります.
\sin{\theta} = y \\
\\
\cos{\theta} = x \\
\\
\tan{\theta} = \frac{y}{x} \\\tan{\theta}は,xの値が1となる相似な三角形を考える方が,分かりやすいときがあります.下の図では\tan{\theta} = y^{\prime} となります.
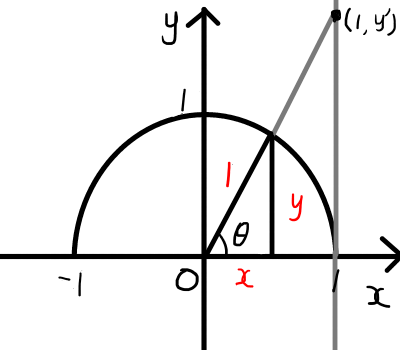
120^{\circ},135^{\circ},150^{\circ}の三角比
90^{\circ} \leqq \theta \leqq 180^{\circ}の三角比で頻出する,120^{\circ},135^{\circ},150^{\circ}の三角比を求めたいと思います.
30^{\circ},45^{\circ},60^{\circ}の三角比とよく似た値になります.次の節の180^{\circ} - \theta とも関係してくるので,じっくり取り組んでみましょう.
まずは135^{\circ}の三角比から求めます.
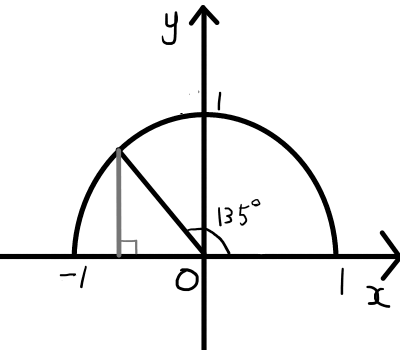
\sin{135^{\circ}} = \frac{1}{\sqrt{2}} \\
\\
\cos{135^{\circ}} = -\frac{1}{\sqrt{2}} \\
\\
\tan{135^{\circ}} = -1 \\
次に120^{\circ}の三角比を求めます.
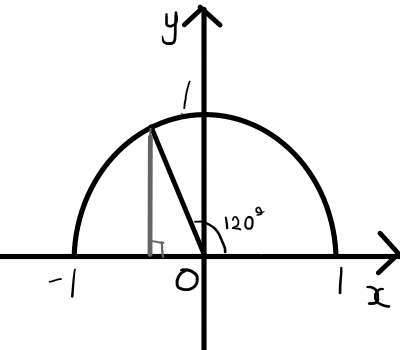
\sin{120^{\circ}} = \frac{\sqrt{3}}{2} \\
\\
\cos{120^{\circ}} = -\frac{1}{2} \\
\\
\tan{120^{\circ}} = -\sqrt{3} \\
最後にまずは150^{\circ}の三角比を求めます.
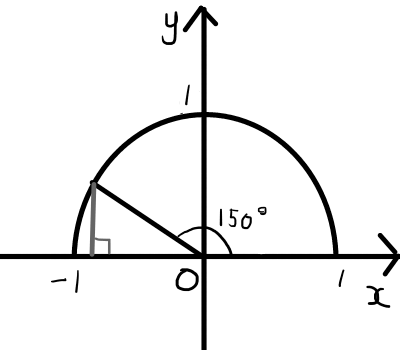
\sin{150^{\circ}} = \frac{1}{2} \\
\\
\cos{150^{\circ}} = -\frac{\sqrt{3}}{2} \\
\\
\tan{150^{\circ}} = -\frac{1}{\sqrt{3}} \\三角比の色々な法則
三角比では様々な等式が成り立ちます.ここではその一部を紹介したいと思います.余角公式などは他の記事で証明する予定です.
90^{\circ} - \theta(0^{\circ} < \theta < 90^{\circ})の三角比について,以下の等式が成り立ちます.
この公式を余角公式と呼ぶことがあります.
\sin{(90^{\circ} - \theta)} = \cos{\theta} \\
\\
\cos{(90^{\circ} - \theta)} = \sin{\theta} \\
\\
\tan{(90^{\circ} - \theta)} = \frac{1}{ \tan{\theta}} \\
また,90^{\circ} + \theta(0^{\circ} \leqq \theta \leqq 90^{\circ})の三角比について,以下の等式が成り立ちます.単位円を使って確かめてみてください.
\sin{(90^{\circ} + \theta)} = \cos{\theta} \\
\\
\cos{(90^{\circ} + \theta)} = -\sin{\theta} \\
\\
\tan{(90^{\circ} + \theta)} = -\frac{1}{ \tan{\theta}}\\
180^{\circ} - \theta(0^{\circ} \leqq \theta \leqq 180^{\circ})の三角比について,以下の等式が成り立ちます.これも単位円を使って確かめてみてください.
また,以下の公式を補角公式と呼ぶことがあります.
\sin{(180^{\circ} - \theta)} = \sin{\theta} \\
\\
\cos{(180^{\circ} - \theta)} = - \cos{\theta} \\
\\
\tan{(180^{\circ} - \theta)} = -\tan{\theta} \\