先に答えが分かる問題
数学の問題では,答えが先に分かり,後から理論が追ってくることがあります.そのようになる理由は様々です.直観で何となく答えが分かる場合もあります.
本記事では,4種類の「先に答えがわかる事例」を用意してみました.
対称性
問題.
40cmの針金を使って長方形を作る.面積が最大となるのはどのような長方形のときか答えよ.
瞬間的に思い浮かんだ答え.
1辺10cmの正方形のとき.
ひとつの考え方として,正方形が答えでないと仮定すると,どちらかの辺を長く,それに合わせてもう一方の辺を短くすると面積が大きくなることになります.そうなると,辺を限りなく長くした方が面積が大きくなるであろうという推測ができ,1辺20cmに限りなく近づける必要がある,つまり明確な答えが出せない状態になるため,正方形以外が答えになることはないだろうと推測できます.
もうひとつの考え方は,線対称の軸の多さです.上記の答えも,こちらの考え方で導き出しています.この考えを端的に言い表した言葉と出会ったので,引用させていただきます.
標語的にいうと,「一番いいのは一番対称性があるものだ」(略)
『数学セミナー3月号』P78 エレガントな解答をもとむ【解答】 vol.61_no.3_725 日本評論社.
この手の問題だと,対称性が最も多いものが答えとなります.よって,答えが正方形だろうと予想ができます.当然ですが,真面目に解答するなら2次関数の最大値を求めましょう.
ちなみにこの問題を以下のように改変すると答えは円となります.円は対称性の塊ですからね.
問題.
40cmの針金を使って自由に図形を作る.面積が最大となるのはどのような図形のときか答えよ.
これは演習問題とするには少し難しいので,気になる人は「等周定理」「等周不等式」で検索してみて下さい.
問題の形式的理由
センター試験や大学入学共通テストのようなマークシート式の問題では,「これしかあり得んやろ」な状況に陥ることがあります.
最たる例として,ベクトルの内積が一桁のときです.ほぼ確実に0が答えです.垂直を使いそうな場合,計算をせずとも「0しかないなぁ」となります.悪問ですね.
正確な図
頭の中で正確な図形を描けたがために,答えが先にわかるケースもあります.
例えば次のような問題です.確か『大学への数学』をパラパラとめくっているときに,見つけた問題だったと思います.
問題.
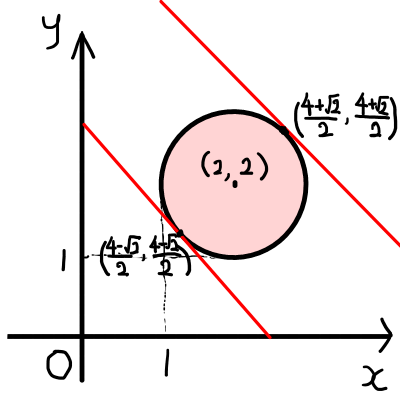
(x-2)^2 + (y-2)^2 \leqq 1におけるx + yの最小値と最大値を求めよ.
これは直線x + y = kが(x-2)^2 + (y-2)^2 = 1と接している状態だということを理解し,頭の中に正確な図を描きます.すると計算なしに接点の座標が分かり,答えが(x,y) = \left( \frac{4- \sqrt{2}}{2}, \frac{4- \sqrt{2}}{2} \right)のとき,x + yの最小値が4- \sqrt{2}となり,(x,y) = \left( \frac{4 + \sqrt{2}}{2}, \frac{4 + \sqrt{2}}{2} \right)のとき,x + yの最大値が4 + \sqrt{2}と分かってしまいました1実際には原点が中心の半径1の円について考えてから,x方向に2,y軸方向へ2動かしたのですが,些細な違いでしょう..
ちょうどその頃マンハッタン距離2いつか記事にすると思いますが,わからない人は検索してね.について考えていましたから,なおさらすぐに分かったのでしょう.
暗記
暗記によって答えが分かることがあります.
私がこのような状況になって苦笑いしたのは,次のような問題です(別々の講義の試験で2回も遭遇しました).
問題1.
4891が素数であるか確かめよ.また,素数でない場合は素因数分解せよ.
問題2.
4331が素数の場合は「素数である」と解答し,素数でなければ素因数分解せよ.
おそらくですが,a=b \times cのとき,b \leq \sqrt{a}かつc \geq \sqrt{a},またはb \geq \sqrt{a}かつc \leq \sqrt{a}が成り立つことを用いて,\sqrt{a}以下の素数で割り切れるか確認していく問題だったのでしょう.そして\sqrt{a}以下の素数を探すにあたって,エラトステネスの篩(ふるい)などを使って,解いてほしかったのでしょう.そのような内容の講義だったと記憶しています.
それに対する私の解答がこちらです.
問題1の解答.
以下のように素因数分解できるため素数ではない.
4891 = 67 \times 73
問題2の解答.
4331 = 61 \times 71
上のような答えしか書いていません.二桁の素数の積をいくつか覚えていたために,こうなってしまいました.好きなんです,二桁の素数の積.
個人的には,数学の暗記は最小限に留めるべきだと考え,試験のための解法パターンの暗記も好きではないのですが,自然と覚えてしまうものは仕方がないと思っています.特に今回のような例は,事故です.

