円と直線の定理
本記事では,円と直線に関する定理を証明します.
円周角
円周角と中心角の定理.
1つの弧に対する中心角は,円周角の2倍である.
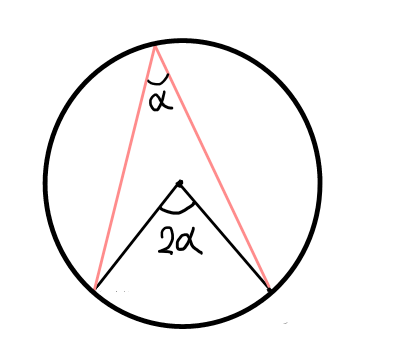
証明.
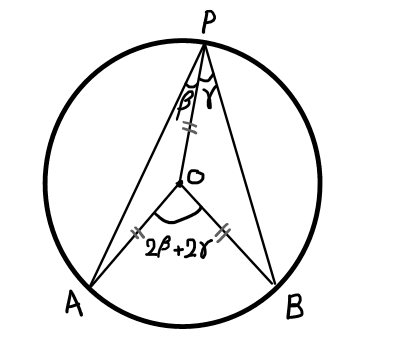
弧を\mathrm{AB}とし,円周上の点を\mathrm{P},円の中心を\mathrm{O}とする.
ここで三角形\bigtriangleup \mathrm{AOP}と\bigtriangleup \mathrm{BOP}に着目する.
\angle \mathrm{APO} = \beta,\angle \mathrm{BPO} = \gammaとすると,2つの三角形は二等辺三角形(2辺の長さが円の半径と等しい)なので,弧\mathrm{AB}の中心角\angle \mathrm{AOB} は2つの三角形の外角の和となる.
つまり,\angle \mathrm{AOB} = 2 \beta + 2 \gamma = 2(\beta + \gamma)である.
一方で弧\mathrm{AB}の円周角\angle \mathrm{APB} = \beta + \gammaより,\angle \mathrm{AOB} = 2 \angle \mathrm{APB} が成り立つ.よって,1つの弧に対する中心角は,円周角の2倍であることが示された.
同一の弧であれば,円周角は必ず中心角の半分になることから,「1つの弧に対する円周角は常に等しい」という定理を導くことができます.
接弦定理
接弦定理.
円の接線と接点\mathrm{A}を通る弦\mathrm{AB}の成す角は,その角の内部に含まれる弧\mathrm{AB}に対する円周角\angle \mathrm{ACB}と等しい.
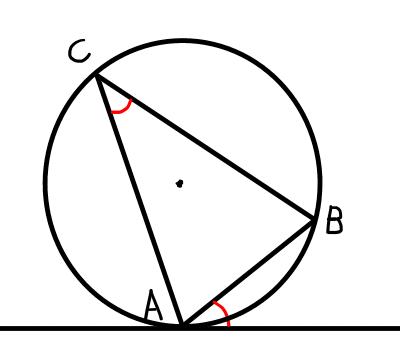
証明.
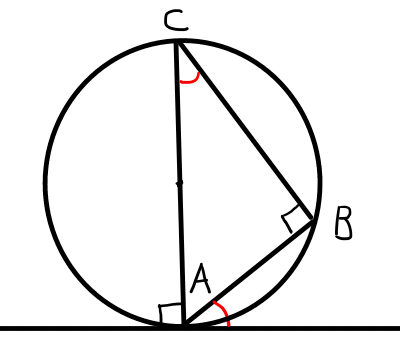
同一の弧の円周角は全て等しいので,\mathrm{AC}が円の中心を通るように,円周上の点\mathrm{C}を移動させる. このとき,円周角と中心角の関係より,\angle \mathrm{ABC} = 90^{\circ}が成り立つ.また,点\mathrm{A}は接点より,\mathrm{CA}と接線の成す角は90^{\circ}である.よって,円の接線と接点\mathrm{A}を通る弦\mathrm{AB}の成す角は, \angle \mathrm{ACB}と等しい.
方べきの定理1
方べきの定理.
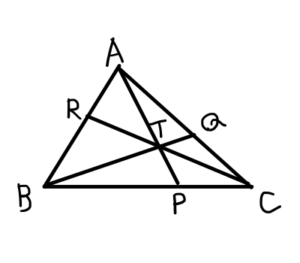
円の2つの弦\mathrm{AB}と\mathrm{CD}の交点\mathrm{P}が円の内部にあるとき,以下の等式が成り立つ.
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}
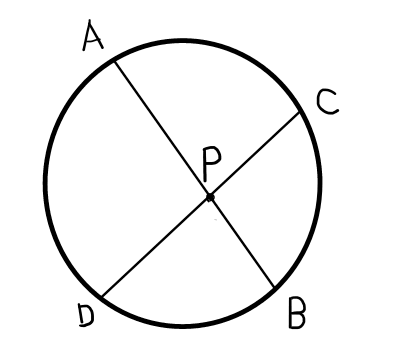
証明.
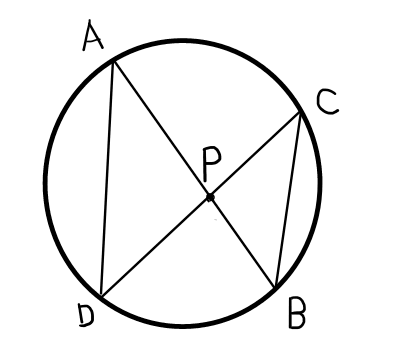
同一の弧の円周角は等しいことから,
\bigtriangleup \mathrm{APD} \text{∽} \bigtriangleup \mathrm{CPB}
よって,
\mathrm{PA} : \mathrm{PC} = \mathrm{PD} : \mathrm{PB}
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}
方べきの定理2
方べきの定理.
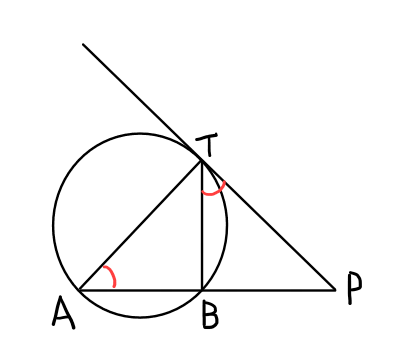
円の2つの弦\mathrm{AB}と\mathrm{CD}の延長の交点\mathrm{P}が円の外部にあり,また点\mathrm{P}から円に引いた接線の接点を\mathrm{T}としたとき,以下の等式が成り立つ.
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD} = \mathrm{PT}^2
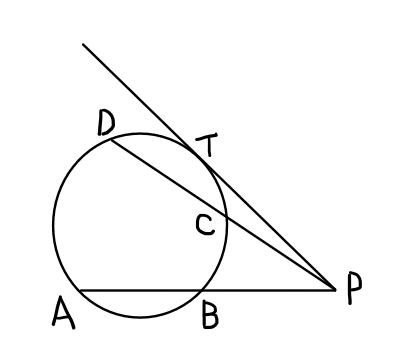
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}の証明.
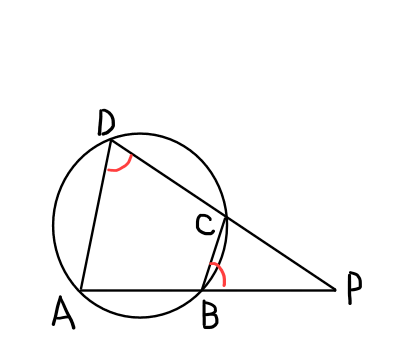
円に内接する四角形\mathrm{ABCD}の性質より,
\angle \mathrm{ADP} = \angle \mathrm{CBP}
したがって,
\bigtriangleup \mathrm{ADP} \text{∽} \bigtriangleup \mathrm{CBP}
よって,
\mathrm{PA} : \mathrm{PC} = \mathrm{PD} : \mathrm{PB}
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PC} \cdot \mathrm{PD}
円に内接する四角形の性質については以下の記事で確認できます.
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PT}^2 の証明.
接弦定理より,\angle \mathrm{TAB} = \angle \mathrm{BTP}が成り立つので,
\bigtriangleup \mathrm{ATP} \text{∽} \bigtriangleup \mathrm{TBP}
よって,
\mathrm{PA} : \mathrm{PT} = \mathrm{PT} : \mathrm{PB}
\mathrm{PA} \cdot \mathrm{PB} = \mathrm{PT}^2