単項式・多項式・整式
中学では,数を文字で表すことを学びました.高校以降の数学でも文字は大活躍します.
この記事では,文字式の重要な言葉を説明していきます.
単項式
次の式を見てみましょう.
-4x^2y^3
この式を指数を使わずに,そして掛け算の記号を省略せずに書いてみます.
-4 \times x \times x \times y \times y \times y
このように,掛け算だけで表すことができました.
-4x^2y^3のように,数と文字の掛け算だけで表される式のことを,単項式と呼びます.
例えば,y^2,3a^2b^8c^3,-p^2q,t^2u^4,は全て単項式です.
また,掛けられている数の部分を係数と呼びます.
単項式 -4x^2y^3 の場合,係数は -4 です.
さて,単項式 y^2 の係数はいくつでしょうか.考えてみましょう.
指数を使わずに y^2 を表すと,
y \times y
となります.数に当たる部分が無いように見えますが,この場合は,
1 \times y \times y
と考え,係数は 1 となります.
では,-p^2q の係数はいくつでしょうか.
答えは文末の注釈でご確認ください1-1 \times p \times p \times qと表せるので,係数は-1です..
多項式
単項式の和で表される式のことを多項式といいます.
例えば,3x^2+ 2xy + y^2 + 4y,2a^2 + 2b^2 + c^3,-p^2q + 5pq^3,x^2-2x + y は全て多項式です.
「x^2-2x + y には引き算が入っているぞ、本当に多項式なのか?」と疑問に思う方もいるでしょう.そこで,この式を x^2 + (-2)x + y と変形してみましょう.こうすると,単項式の和の形で表されている,つまり多項式であることが分かります.
多項式を構成する単項式,つまり,足し算で繋げられているパーツのことを項といいます.
4x^2 - 3xy + 2y^3 + 4y -5 という多項式を見てみましょう.
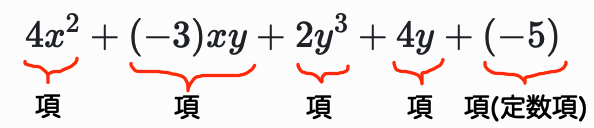
この多項式の場合,4x^2, - 3xy , 2y^3 , 4y,-5 がそれぞれ項となります.また,-5の項のように,数だけの項のことを定数項といいます.さらに,項ごとに係数を考えることができ,例えば,「x^2 の項の係数は 4」「4x^2 の項の係数は 4」といった表現ができます.
次に,以下の多項式を見てみましょう.
2a^2b^2 - 3a^2 + b^2 + 4ab -2b + 9 + 3a^2b^2 - 5ab
これまでに紹介した多項式と違い,文字の部分が同じ項があります.「2a^2b^2」と「3a^2b^2」,「4ab」と「- 5ab」がそれに当たります.
文字の部分が同じ項のことを同類項と呼びます.同類項は,以下のように計算してまとめることができます.
2a^2b^2 - 3a^2 + b^2 + 4ab -2b + 9 + 3a^2b^2 - 5ab
= 2a^2b^2 + 3a^2b^2 - 3a^2 + b^2 + 4ab - 5ab -2b + 9
= (2 + 3)a^2b^2 - 3a^2 + b^2 + (4 - 5)ab -2b + 9
= 5a^2b^2 - 3a^2 + b^2 -ab -2b + 9
また,多項式をある文字に着目して次数の高い項から順に並べることを,降べきの順に整理すると言います.例えば,3x^2y -2 + 2x - 3x^3 +9x^4 を x の降べきの順に整理すると,9x^4 - 3x^3 + 3x^2y + 2x -2 となります.
逆に,次数の低い項から順に並べることを,昇べきの順に整理すると言います.
整式
単項式と多項式を合わせて,整式と呼びます.
ここからの内容は大きな寄り道、余談となります.
「次数」の節まで飛ばしていただいても問題ありません.
「整式」という呼び方は,高校数学以外ではあまり見かけないため,高校生の間だけ覚えておき,大学受験が終わると同時に忘れてしまっても良いでしょう.というのも,大学以降の数学では,多くの場合,多項式が単項式を含むように定義されるからです.つまり,高校数学の「整式」と同じ意味で「多項式」が使われるようになります.
また,整式という名前は,「整数のような性質を持っている文字式」であることが由来だと思われます.このことは後々の学習で分かってくると思います.
高校数学ではあまり触れられませんが,多項式には指数部分の数2x^2の2の部分が0以上の整数であるという条件があります.x^{-2} のような項が含まれることを認めない,というわけです.そのため,多項式の次数3次の節で解説します.は0以上の整数となります.この条件に対して,負の冪乗4-2乗とかも認めるローラン多項式というものがあります.数学科に行けば,ローラン多項式と出会えるかもしれませんね.
次数
次に,次数について説明します.
単項式の次数は,掛けられている文字の数のことです.
-4x^2y^3 の場合だと,x が2個,y が3個掛けられているため,文字の数は合わせて5個,つまり次数は5になります.
多項式や整式の場合は,最も次数の高い項の次数が,その多項式(整式)の次数となります.
例として,4x^2 - 3xy + 2y^3 + 4y -5 を見てみましょう.それぞれの項の次数は,左の項から順に,2,2,3,1,0であり,最も大きいのは3なので,この多項式の次数は3となります.
特定の文字に着目する
2種類以上の文字がある式では,特定の文字にだけ着目して,それ以外の文字を数とみなすことがあります.
例)
4x^2 - 3xy + 2y^3 + 4y -5 は,次数 3,定数項 -5 の整式です.しかし,x に着目し,それ以外の文字を数とみなした場合は,次数2,定数項 2y^3 + 4y -5 の整式となります.
この考え方が有効な場面は度々ありますので,使いこなせるようによく練習しておくと良いでしょう.
変数・未知数・定数
この記事では「文字」という言葉を使用していますが,ひと口に文字と言いましても,その役割によってふさわしい名前があります.変数,未知数,定数という3つの言葉について知っていても損はしないでしょう.
説明するのが面倒なので,3つの言葉の違いに関しては,こちらのページやWikipediaの変数のページ冒頭を読むと良いかと思います.

