大学入試共通テスト「情報Ⅰ」サンプル問題の解説(第3問)
この記事は上記記事の続きです.
大学入学共通テストの「情報Ⅰ」サンプル問題について解説をします.
第2問の解説はする気がないので1プログラムは書いた通り動きます.コードを書く人,読む人の考えは全く関係ありません.解説終わり.,第3問を解説をします.
第3問全体の概観
ある年のワールドカップの参加チームのデータを,決勝進出チームと予選敗退チームに分けて分析するという内容です.
数学Ⅰの「データの分析」の単元と被っている内容も多いので,数学Ⅰの学習も積極的に行いましょう.
問1
問1 a
ア・イ
正答は0と3になります.
予選敗退チームでは相関関係がほとんど無い組み合わせは「得点とロングパスの本数」,「得点と反則回数」,「ロングパスの本数と反則回数」の3つの組み合わせです.このうち決勝進出チームでは負の相関がある組み合わせは「得点と反則回数」のみとなります.
ウ
正答は3になります.
相関係数の符号が逆符号であり,その差が最も大きくな っている組み合わせは,「ショートパスの本数とロングパスの本数」の組み合わせです.「ショートパスの本数とロングパスの本数」の散布図はDとなります.
問1 b
エ
正答は2となります.
「正の相関がある」と言える範囲は状況や分野により異なりますので,とりあえず最も広く捉えて,相関係数が正の組み合わせを探します.相関係数が正の組み合わせは「得点とショートパスの本数」,「得点とロングパスの本数」,「ショートパスの本数とロングパスの本数」の3つの組み合わせです.このうち,決勝進出チーム,予選敗退チームのいずれも相関係数が負の組み合わせは存在しないため,2が誤りであることが分かります.
問2
問2は単回帰分析の問題となります.1試合あたりのショートパスの本数 x から,1試合あたりの得点 y を予測するモデルとなっています.決勝進出チームと予選敗退チームのそれぞれに対して,予測モデルを考える問題です.
オカ
正答は16となります.
問われているのは得点の増加量なので,回帰モデルの x の係数に着目します.
決勝進出チームの x の係数は 0.0080 ,100倍すると 0.8 となります.つまり,ショートパス100本あたりの得点の増減量は 0.0080 であることが分かります.同様に予選敗退チームの x の係数は 0.0064 ,100倍すると 0.64 となります.
よって,ショートパス 100 本につき,1試合当たりの得点増加数の差は, 0.8 - 0.64 = 0.16 となります.
キ
正答は4となります.
決勝進出チームと予選敗退チームの得点予測の差を求める問題です.この問題では320本の場合を考えています.
決勝進出チームの回帰モデルの x に 320 を代入すると, 0.0080 \times 320 - 1.4307 = 2.56 - 1.4307 = 1.1293 となり,予測値は 1.1293 です.
同様に,予選敗退チームの回帰モデルの x に 320 を代入すると, 0.0064 \times 320 - 0.9567 = 2.048 - 0.9567 = 1.0913 となり,予測値は 1.0913 となります.
小数第3位を四捨五入してその差を計算すると, 1.13 - 1.09 = 0.04 となります.
クケ
正答は56となります.
決勝チームの回帰モデルの予測誤差を計算する問題です.
決勝進出チームの回帰モデルの x に 384.2 を代入すると, 0.0080 \times 384.2 - 1.4307 = 3.0736 - 1.4307 = 1.6429 となり,予測値は 1.6429 です.
実際の値は 2.20 なので,その差は 2.2 - 1.6429 = 0.5571 小数第3位を四捨五入して 0.56 となります.
問3
問3はさまざまな統計量について,正確に記述している文を選ぶ問題です.
コサ
正答は0と3となります.
1番は「1試合あたりのショートパスの本数」中央値(第2四分位数)と平均値を比べる内容です.決勝進出チームは平均の方が大きいのでこの選択肢は誤りです.
2番は「1試合当たりのショートパス本数を見る」と,決勝進出チームの第1四分位数は予選敗退チームの中央値より大きいため誤り.
4番は「1試合当たりの反則回数」の予選敗退チームの第1四分位数は,決勝進出チームの中央値より大きいため誤りとなります.
誤りの選択肢がとても分かりやすく間違ってくれているので,消去法を使うと自信を持って答えることができる問題です.
問4
問4はこれまでの図表から正しい内容の文を選択する問題が1題,残りはリード文を読みながらクロス集計表の穴埋めをする問題となっています.
シ
正答は3となります.
0番は「1試合当たりの反則回数が」最も多いチームは予選敗退チームであるため誤り(図1参照).
1番は「1試合当たりの反則回数」と「1試合当たりの得点」の間には,全参加チームにおいて負の相関があるため誤り(図1参照).
2番は「1試合当たりの反則回数」と「1試合当たりの得点」の間には,予選敗退チームに負の相関が無いため誤り(図1参照).
ス
正答は4となります.
まず問題中のクロス集計表が以下の様に穴あき状態になっています.
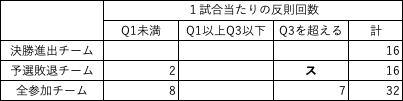
文章中に「決勝進出チームのうち1試合当たりの反則回数が全参加チームにおける第3四分位数を超えるチームの割合は約19%であった」とあることから,表中の「決勝進出チーム」で「Q3を超える」に入る数値は,16 \times 0.19 = 3.04 より 3 であることが分かります.
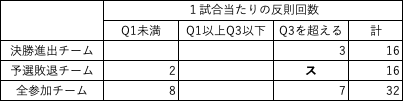
よってスに入る数値は 7 - 3 = 4 で 4 となります.
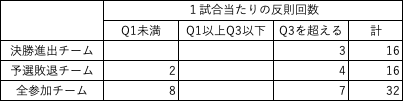
セソ
正答は75となります.
「1試合当たりの反則回数がその第1四分位数より小さいチームの中で決勝進出したチームの割合」を求める問題です.
まずは「決勝進出チーム」で「Q1未満」に入る数値 8 - 2 = 6 を求めます.

「1試合当たりの反則回数がその第1四分位数より小さいチームの中で決勝進出したチームの割合」は,
\begin{aligned} \frac{6}{8} = 0.75 \end{aligned}
よって75%が答えとなります.