展開公式の覚え方
「あれ?ここはマイナスだっけ?プラスだっけ?」
「係数は-1だっけ?-2だっけ?」
このように,展開公式(乗法公式)を思い出すのに手こずった人もいるでしょう.
この記事は,公式を覚えるのに悪戦苦闘している人のために書きました.
3つの覚え方を紹介したいと思います.
そもそも展開公式とは?
モチベーションを上げるために,展開公式の利点について説明します.
展開公式(乗法公式)とは,特定の形の展開を楽にするための公式です.
展開とは,複数の整式の積を1つの整式にする操作であり,分配法則1A(B+C)=AB + AC \\ (A+B)C = AC + BCを用いて計算することができます.しかし,ある形式の整式の積は,特徴的な計算結果となります.それらをまとめたものが展開公式です.
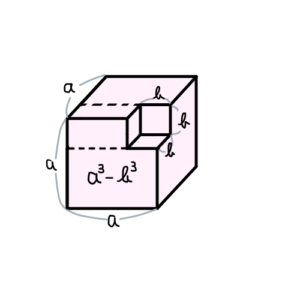
覚え方1. 図で覚える
1つ目の方法は,図を使って視覚的なイメージで覚える方法です.
例えば,以下の図は,一辺(a+b)の正方形の面積が,a^2 + 2ab + b^2と表されることを示しています.この図を見れば(a+b)^2 = a^2 + 2ab + b^2であることが感覚的に分かります.

参考過去記事:展開公式を図示する
全ての展開公式を図示できるわけではありませんが,基本的な公式は押さえることができます.
覚え方2. 一般的な公式だけ覚える
一般的な形の公式だけ覚えて,そこから他の公式を導き出すという方法があります.
数学Ⅱや数学Aの知識が必要になりますが,以下に示す二項定理
(a+b)^n = {}_n \mathrm{C}_0 a^nb^0 + {}_n \mathrm{C}_1 a^nb^1 + \cdots + {}_n \mathrm{C}_{n-1}a^1 b^{n-1} + {}_n \mathrm{C}_n a^0b^n
を覚えていれば,
(a+b)^2 = a^2 + 2ab + b^2
(a+b)^3 = a^3 + 3a^2b +3ab^2 + b^3
(a+b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
などを瞬時に導くことができます.
さらに,これらの公式の bに -b を代入することで,
(a-b)^2 = a^2 - 2ab + b^2
(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3
(a-b)^4 = a^4 - 4a^3b + 6a^2b^2 - 4ab^3 + b^4
を求めることができます.
また,(a+b)^2 = a^2 + 2ab + b^2のbにb+cを代入すると,
\{a+(b+c)\}^2 = a^2 + 2a(b+c) + (b+c)^2=a^2 + b^2 + c^2 + 2ab +2bc +2ca
を求められます.
他にも,以下の公式から,多くの公式を求めることができます.
(a-b)(a^{n-1}b^0 + a^{n-2}b^1 + \cdots + a^1b^{n-2} + a^0b^{n-1}) = a^n - b^n
n = 2 のとき
(a+b)(a-b) = a^2 - b^2
n = 3 のとき
(a-b)(a^2 + ab + b^2) = a^3 - b^3
n = 4 のとき
(a-b)(a^3 + a^2b + ab^2 + b^3) = a^4 - b^4
さらに,nが奇数のときに,bに-bを代入してみましょう.
n = 3 のとき
(a+b)(a^2 - ab + b^2) = a^3 + b^3
別の展開公式を得ることができます.
覚え方3. 問題を解きまくる
最後は,問題を解きまくって覚える方法です.
自然と覚えるまで解き続ければOKというわけですね.
まとめ
以上,3つの覚え方を紹介しました.
使っているうちに自然と覚えるものなので,身構えず楽にいきましょう.
それと最後にひとつ.
「展開しなさい」という問題であれば,公式を思い出せなくても大丈夫です.分配法則2A(B+C)=AB + AC \\ (A+B)C = AC + BCを用いて,ゴリ押ししましょう.
展開公式は,特定の形式の展開を楽にするための公式なので,困ったら分配法則で苦労しながら解くのもアリなのです.