展開公式を図示する

展開公式（乗法公式）のひとつに(a+b)^2=a^2 + 2ab + b^2があります．この公式を視覚的に分かりやすくしたものとして，以下のような図が有名です．

一辺(a+b)の正方形の面積がa^2 + 2ab + b^2と表せることが分かります．
このような図は，厳密な証明などには使えませんが，展開公式の理解の手助けになることは確かです．

この記事では，他の展開公式の図も描いてみたいと思います．

(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca

(a+b)^2=a^2 + 2ab + b^2と同じ要領で，(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2caを図示してみましょう．

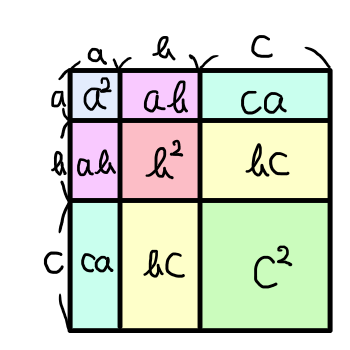
なかなか分かりやすい図ですが，少しごちゃごちゃしてきました．
文字の種類を増やすのは止めにしましょう．

(a+b)(a-b)=a^2-b^2

次に，(a+b)(a-b)=a^2-b^2の図を描いてみます．

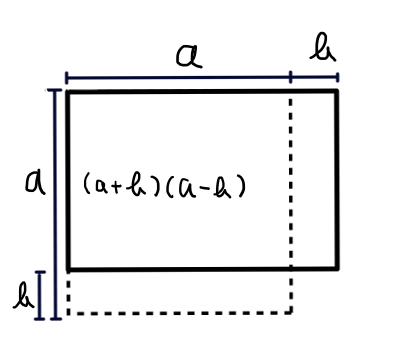
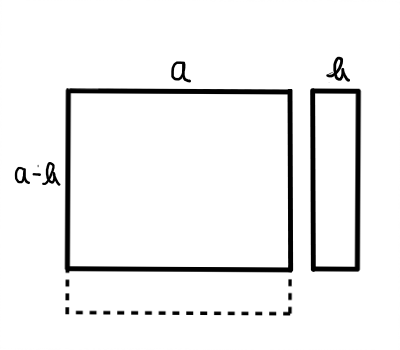
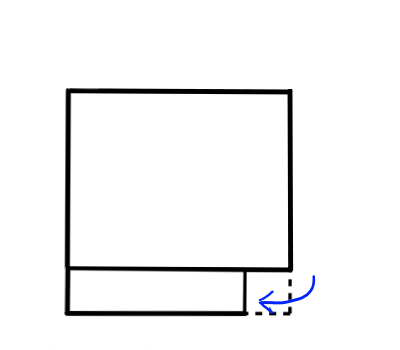
少し動きが出てきましたが，これも分かりやすいですね．

(a+b)^3=a^3+3a^2b+3ab^2+b^3

次は3次の展開公式を図示してみます．
(a+b)^3=a^3+3a^2b+3ab^2+b^3

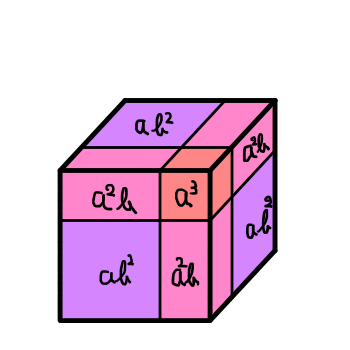
なるほど，これを理解しやすいと感じるかは，立体を頭の中で動かして，裏側に隠れたb^3を見る能力があるかによりそうです．3Dモデルを作って，くるくる回してみた方が万人受けするかもしれません．

(a-b)(a^2+ab+b^2)=a^3-b^3

最後に，(a-b)(a^2+ab+b^2)=a^3-b^3の図を描いてみます．

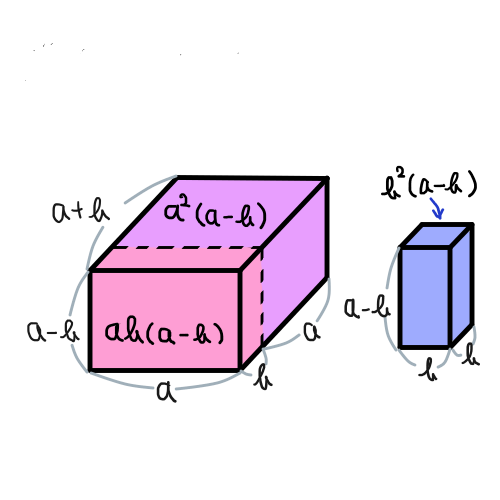
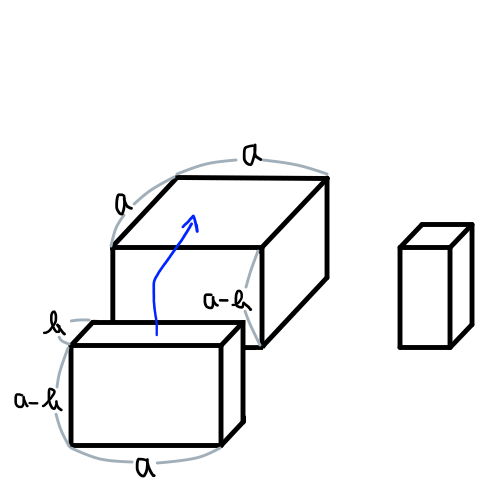
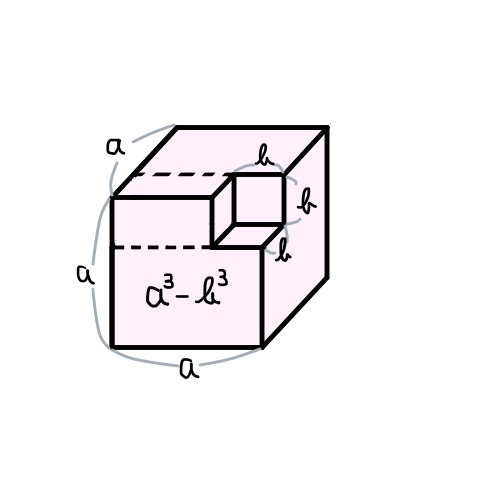
動きの理解に少し時間がかかるかもしれません．
それと，だんだんと図が理解の助けにならなくなってきました．

これ以上複雑な公式を，分かりやすい図として描くのは難しいかもしれません．

遊びの提案（演習問題）

1. (a+b+c)(a^2+b^2+c^2-ab-bc-ca)=a^3+b^3+c^3-3abcの図を描いてみましょう（できるだけ理解の手助けとなるようなものを）．
2. この記事に出てこなかった展開公式の図も描いてみましょう．
3. 記事の冒頭に「（図は）厳密な証明には使えませんが」とあります．このような図が証明に使えない理由を考えてみましょう．

1番ができた人は教えてください．ぜひ，見たいです．

（追記）2022年3月24日

3次の展開公式のアニメーションを作りました！

3次の展開公式の図を動かしてみた

　

「勝手気ままに高校数学」シリーズ一覧へ