弧度法 〜ラジアンの定義〜
高校数学では,三角関数を学ぶ前に2つの概念を導入します.それが一般角と弧度法です.
前回の記事では一般角について解説しましたので,本記事では弧度法についての解説をします.
弧度法
半径rの円上に長さがrになるような弧\mathrm{AB}を取ります.このとき,弧\mathrm{AB}に対する中心角の大きさを1ラジアンといいます.1ラジアンの大きさは,半径の長さに関わらず一定です.この1ラジアンを基準として,弧の長さと半径の比を用いて角度を表す方法を弧度法といいます.(弧の長さ)\div(半径)で求められます.弧度法の単位はラジアン(rad)ですが,単位を省略して書かれることが多いです.
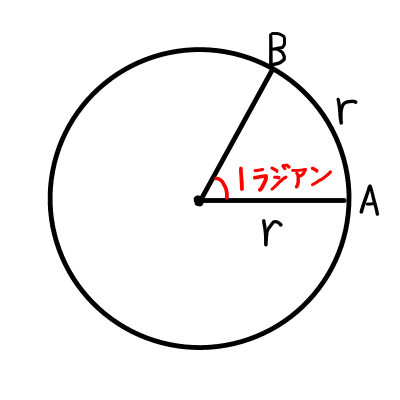
また,これまで用いてきた30^{\circ}のような表現の仕方を度数法といいます.
ちなみに2018年のセンター試験1現在の大学入学共通テストで,1ラジアンの定義を答える問題が出題されたことがあります.選択肢のある問題ですし,基本中の基本ですから,ほぼ全員正答していることでしょう2願望であり,同時に煽りでもあります.あの問題を間違える人間は,もし他の問題が全問正答であっても数学をしていません.三角関数を勉強していなかった可能性もありますが,そうでなければ公式と解法を暗記する機械になっていたのでしょう..
ここまでの説明を読んで,「なぜ弧度法を使うのか」と疑問に思われた方もいるでしょう.大変素晴らしい疑問だと思います.しかしその疑問は一度忘れてしまいましょう.度数法が不便だったり,弧度法の方が綺麗な公式が出てきたりするのですが,そういった良さが分かるのは先々の話なので,まずは弧度法をしっかりマスターしましょう3そのうち記事を書くかもしれません..
弧度法で表された角度の例
先述しましたが再び,弧度法による角度の大きさの求め方をまとめたいと思います.弧の長さをl,円の半径をrとすると中心角の角度は,\frac{l}{r}と表されます.例えば,半径2,弧の長さが\piのとき,中心角は\frac{\pi}{4}ラジアンとなります.
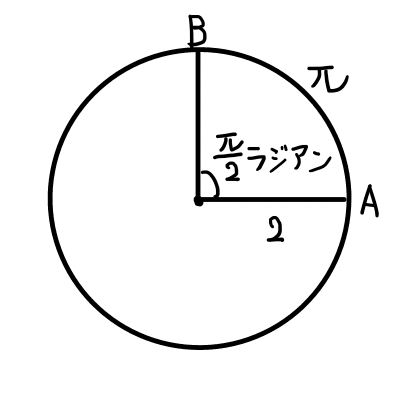
では以下の図のような場合はどうでしょうか.
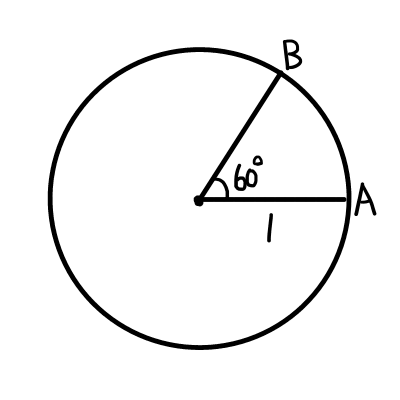
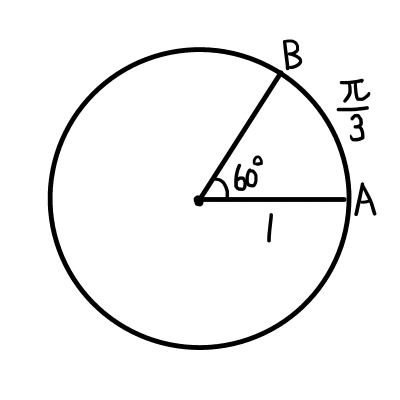
中心角が60^{\circ}なので,半径を1とすると,弧の長さは2 \pi \div \frac{60^{\circ}}{360^{\circ}} = \frac{\pi}{3}
となります.つまり,この角度を弧度法で表すと\frac{\pi}{3}ラジアンとなります.
弧度法と一般角
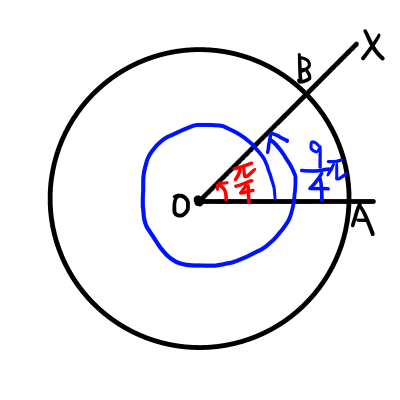
度数法のときと同様に,弧度法においても一般角を考えることができます.
度数法のときと同様に,始線から左回転を正の角,右回転を負の角とします.
始線と動径の間の角を求める場合,始点と動径の共通点\mathrm{O}を中心とする円を考えることで角度を求めることができます.
2 \piで1回転となるため,
\theta + 2 \pi \times n (nは整数)の動径は一致します.
例を挙げると,\frac{\pi}{4}と\frac{9 \pi}{4}の動径は一致します.
弧度法と度数法
2節前に,中心角60^{\circ}を弧度法で表しました.
弧度法のよる表記と度数法による表記は,相互に変換することができます.
ここでは30^{\circ}を弧度法で表してみましょう.
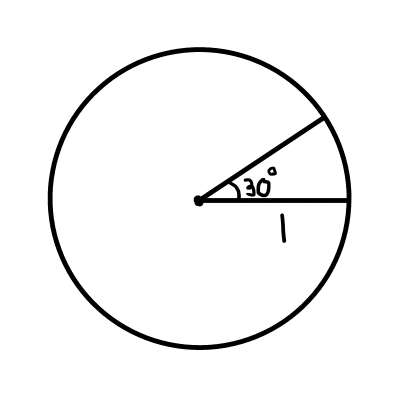
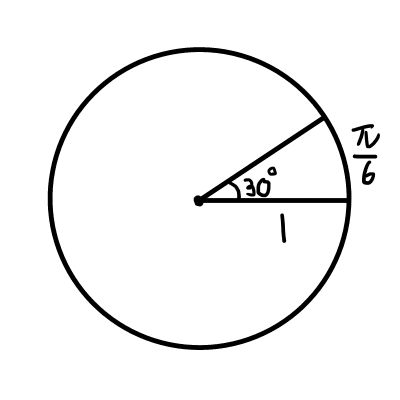
この長さを求めると,
\begin{aligned}
\frac{30^{\circ}}{360^{\circ}} \cdot 2 \pi &= \frac{\pi}{6} \\
\end{aligned}
半径は1なので,30^{\circ}は\frac{\pi}{6}ラジアンです.
この過程を一般化してみましょう.中心角の度数法表記を\thetaとすると,円の半径が1の場合,弧の長さが\frac{\theta}{360^{\circ}} \cdot 2 \pi = \frac{\theta}{180^{\circ}} \cdot \piとなります.度数法の表記に\frac{\pi}{180^{\circ}}を掛けると弧度法による表記になることが分かりました.
ちなみに,弧度法と度数法の変換の問題が,同じく2018年のセンター試験で出題されました.計算量も少ないので,出題されるとラッキーな問題ですね.
最後によく使われる角度について,度数法と弧度法の表記をまとめます.
| 度数法 | - 90^{\circ} | - 60^{\circ} | -45^{\circ} | - 30^{\circ} | 0^{\circ} | 30^{\circ} | 45^{\circ} | 60^{\circ} | 90^{\circ} | 120^{\circ} | 135^{\circ} | 150^{\circ} | 180^{\circ} | 210^{\circ} | 225^{\circ} | 240^{\circ} | 270^{\circ} | 360^{\circ} |
| 弧度法 | - \frac{\pi}{2} | - \frac{\pi}{3} | - \frac{\pi}{4} | - \frac{\pi}{6} | 0 | \frac{\pi}{6} | \frac{\pi}{4} | \frac{\pi}{3} | \frac{\pi}{2} | \frac{2}{3} \pi | \frac{3}{4} \pi | \frac{5}{6} \pi | \pi | \frac{7}{6} \pi | \frac{5}{4} \pi | \frac{4}{3} \pi | \frac{3}{2} \pi | 2 \pi |
数Ⅲや大学数学を覗いてみよう!
厳密な数学では,弧度法を定義する前にするべきことがあります.というのも,弧度法には「曲線の長さを測る(求める)ことができる」という前提条件があるからです.一見すると成り立って当たり前の条件に見えるかもしれませんが,歴史的に見ると,曲線の長さを求めることは必ずしも容易ではありませんでした.
というわけで厳密にやるならば,弧度法を導入する前に,曲線の長さを求める手法が必要となります.
曲線の長さを求める基本的な方法については,数学Ⅲで学びます.
そのうち記事にしますが,気になる方は「弧長」で検索してみてください.

