1-2. 整式の掛け算(展開)　〜展開公式とその応用〜

例題1の解答．
(1)
-2(a + b + c) \\ = -2 \times a + (-2) \times b + (-2) \times c \\ = -2a -2b -2c

(2)
-4x(x -2y + z) \\ =-4x \times x + (-4x) \times (-2y) + (-4x) \times z \\ = -4x^2 + 8xy - 4xz

(3)
3a^2b(4a^2 - 2ab + 3b^2) \\ = 3a^2b \times 4a^2 + 3a^2b \times (- 2ab) + 3a^2b \times 3b^2 \\ = 12a^4b - 6a^3b^2 + 9a^2b^3

(4)
3xy(x + 3xy -2y^2) \\ = 3xy \times x + (3xy)^2 + 3xy \times (-2y^2) \\ = 3x^2y + 9x^2y^2 - 6xy^3

(5)
21abc(11a - 4b - 6c + 3d) \\ = 21abc \times 11a + 21abc \times (- 4b) + 21abc \times (-6c) + 21abc \times 3d \\ = 231a^2bc - 84ab^2c - 126abc^2 + 63abcd

(6)
(a + b)(a + c) \\ = a(a + c) + b(a + c) \\ = a^2 +ac +ab + bc

解答．
(1) (2x + y)^2 = 4x^2 + 4xy + y^2
(2) (3a - b)^2 = 9a^2 - 6ab + b^2
(3) (4x - 9)^2 = 16x^2 -72x + 81
(4) (3x + 2y)(3x - 2y) = 9x^2 - 4y^2
(5) (9a + 11b)(9a - 11b) = 81a^2 -121b^2
(6) (2x + 3)(x - 4) = 2x^2 - 5x -12

解説．
(1) は (a + b)^2 = a^2 + 2ab + b^2 の公式を使います．

(2) と (3) は (a - b)^2 = a^2 - 2ab + b^2 の公式を使います．

(4) と (5) は (a + b)(a - b) = a^2 - b^2 の公式を使います．

(6) は (ax + b)(cx + d) = acx^2 + (ad + bc)x + bd の公式を使います．もう少し丁寧に途中式を書くと以下のようになります．
\begin{aligned} (2x + 3)(x - 4) &= 2x^2 + (2 \times (-4) + 3 \times 1)x + 3 \times (-4) \\ &= 2x^2 - 5x - 12 \end{aligned}

解答．
(1) (3x + y + 2z)^2 = 9x^2 + y^2 + 4z^2 +6xy +4yz +12zx
(2) (a - 2b - 5)^2 = a^2 + 4b^2 + 25 - 4ab + 20b + 10a = a^2 + 4b^2 - 4ab + 10a + 20b + 25

(2) は最後の並び替えが無くても問題ありません．

　公式 (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca を見て違和感を覚えた人が居るかもしれません．なぜ最後の項の ca は ac と書かないのでしょうか．その理由はこの式の後半が輪環の順によって整理されているためです．

　ここでは最も頻出する，文字が3種類の輪環の順について解説します．輪環の順のポイントは文字を循環させることです．
　以下の3つの式を見てみましょう．これらの式を見て，どのように感じましたか．

ab + bc + ac
ab + ac + bc
ab + bc + ca

　ab + bc + ac という書き方は乱雑な感じがしますね．並びに規則性が感じられません．
　ab + ac + bc は辞書のような並び方です²これでもいい気がします．a に関する降べきの順と考えると，完璧な並びとなっています．
　ab + bc + ca は前の項の最後の文字と，次の項の最初の文字が同一になっています．ab \rightarrow bc \rightarrow ca \rightarrow ab \rightarrow \cdots \cdots と，どこまでも続いて行きそうです．このようにアルファベット順にグルグルと循環させる並べ方のことを輪環の順といいます．輪環の順はミスをしにくく，見やすいと言われている並べ方です．

ab, bc, ca の組み合わせの他にも，a + b, b + c, c + a や a - b, b - c, c - a の組み合わせがあります．³余談ですが，後のページで学習する「交代式」では， (a - b)(b - c)(c - a) が重要な役割を果たします．

　降べきの順とは異なり，輪環の順に整理しなければならない理由はありませんが，定期試験では輪環の順に整理しないと減点してくる採点者がたまにいるので気をつけましょう！
　筆者は高校時代に，輪環の順に整理していないという理由だけで大幅減点をくらった経験があります．輪環の順，好きではありません．ついでに高校数学もしばらく嫌いになりました．
　この記事を読んでいる高校教育の関係者がいましたら，愚かな理由での減点は絶対にやめてください！数学の本質とかけ離れた事情による減点は，数学嫌いが増える原因になります！

（2024/1/18）かなり歪んだ主観が含まれていたため，コラムを修正しました．戒めのために修正前のコラムを以下に残します．

修正前のコラムを見る

コラム：輪環の順
*･゜ﾟ･*:.｡..｡.:*･'(*ﾟ▽ﾟ*)’･*:.｡. .｡.:*･゜ﾟ･
*☆*:.｡. o(≧▽≦)o .｡.:*☆⁴こんな気持ち悪いタイトルになっていることには，正当な理由があります．

　公式 (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca を見て違和感を覚えた人が居るかもしれません．なぜ最後の項の ca は ac と書かないのでしょうか．その理由は ただのカッコつけ この式の後半が輪環の順によって整理されているためです．

　ここでは最も頻出する，文字が3種類の輪環の順について解説します．輪環の順のポイントはなんかグルグルしそうなことです．
　以下の3つの式を見てみましょう．

ab + bc + ac
ab + ac + bc
ab + bc + ca

　ab + bc + ac という書き方は乱雑な感じがしますね．b に関する降べきの順にでもしたのかと疑うほどグチャグチャしています．
　ab + ac + bc は辞書のような並び方です⁵これでいいんじゃないかな？．
　ab + bc + ca は前の項の最後の文字と，次の項の最初の文字が同一になっています．ab \rightarrow bc \rightarrow ca \rightarrow ab \rightarrow \cdots \cdots と，どこまでも続いて行きそうです．このようにアルファベット順にグルグルさせた並べ方のことを輪環の順といいます．輪環の順はミスをしにくく，見やすい とか言われていますが，要は「どうだぁ，カッコイイだろぉ！」って感じの 並べ方です．

ab, bc, ca の組み合わせの他にも，a + b, b + c, c + a や a - b, b - c, c - a の組み合わせがあります．

　降べきの順とは異なり，別に輪環の順に整理しなければならない理由はありませんが，定期試験では輪環の順に整理しないと減点してくるアホがたまにいるので気をつけましょう！
　お察しの方もいらっしゃると思いますが，筆者は高校時代に輪環の順に整理していないという理由だけで大幅減点をくらった経験があります．輪環の順，嫌いです⁶だからこんなにも雑でふざけた解説なんです．．ついでに高校数学もしばらく嫌いになりました．
　この記事を読んでいる高校の先生がいらっしゃいましたら，アホな理由で減点するのは絶対にやめてください！数学の本質とかけ離れた事情による減点は，数学嫌いが増える原因になります！

　2次の展開公式は，演習問題を解いているうちに覚える人が多いと思います．それでも，どうしても覚えられない人のために，以下のような図で覚える方法を紹介したいと思います．ちなみに，同様の内容をこちらの記事でも解説しているので，読んでいただけますと幸いです．

　それでは (a + b)^2 = a^2 + 2ab + b^2 について説明しましょう．(a + b)^2 = a^2 + 2ab + b^2 の場合は，一辺の長さが a + b の正方形の面積を考えます．このとき，面積の表し方が複数あります．もっともシンプルなのは，(a + b)^2 と表すものです．また，以下の図を見て正方形の面積について考えてみましょう．

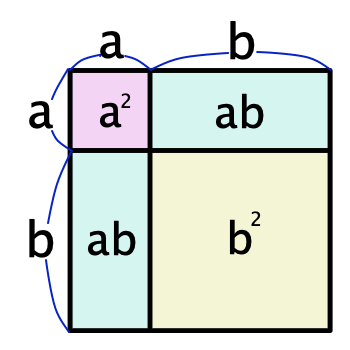
正方形の面積を a^2 + 2ab + b^2 と表すこともできます．ここから (a + b)^2 = a^2 + 2ab + b^2 であることを理解できるかと思います．

　気をつけていただきたいのですが，この説明は (a + b)^2 = a^2 + 2ab + b^2 を理解するための図であり，決して公式の証明にはなり得ないということを忘れないでください．「負の数の場合は？」や「複素数の場合は成り立つの？」など，図だけでは示せないことがあるでしょう．なんなら，a = b や，a > b となるケースもこの図では示せていません．図はあくまで図です．理解を助けるための道具であることをお忘れなく．

　同様に (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca についても，正方形の面積として考えることができます．

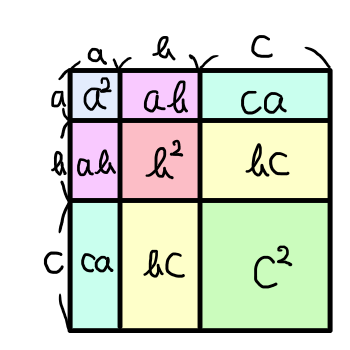
上の図から，一辺 a + b + c の長方形の面積を，(a + b + c)^2 と a^2 + b^2 + c^2 + 2ab + 2bc + 2ca の2通りで表せることが分かります．ここから (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca に結びつけることができます．

　最後に (a + b)(a - b) = a^2 - b^2 を図で捉える方法について説明します．これも図形の面積を考えます．多少動きがありますが，以下の4つ図を見れば納得できるかと思います．

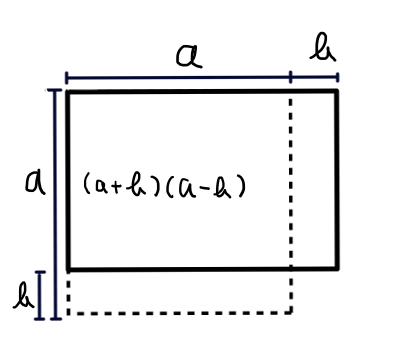
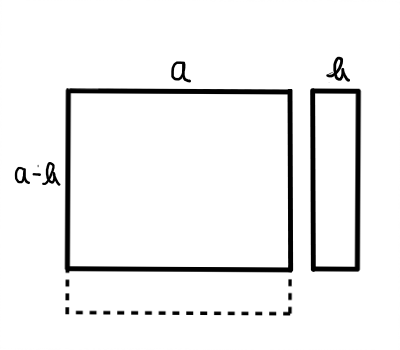
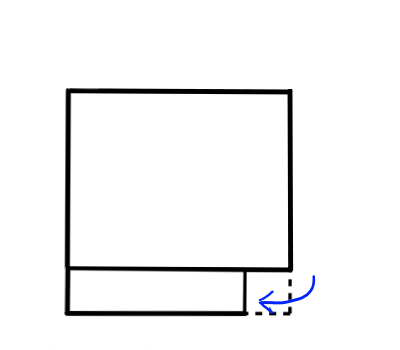
　さて，このコラムを読んでいる人に課題です．(a - b)^2 = a^2 - 2ab + b^2 を図で表してみましょう．

解答．
(1) (2x + y)^3 = 8x^3 + 12x^2y + 6xy^2 + y^3

(2) (3a - b)^3 = 27a^3 - 27a^2b + 9ab^2 - b^3

(3) (3x - 4)^3 = 27x^3 - 108x^2 + 144x - 64

(4) (3x + 2y)(9x^2 - 6xy + 4y^2) = 27x^3 + 8y^3

(5) (3a - 4b)(9a^2 + 12ab + 16b^2) = 27a^3 - 64b^3

(6)
(a + b + c)^3 \\ = \{ (a + b) + c \}^3 \\ = (a + b)^3 + 3(a + b)^2 c + 3(a + b)c^2 + c^3 \\ = a^3 + 3a^2b + 3ab^2 + b^3 + 3ca^2 + 6abc + 3b^2c + 3c^2a + 3bc^2 + c^3 \\ = a^3 + b^3 + c^3 + 3a^2b + 3ab^2 + 3b^2c + 3bc^2 + 3c^2a + 3ca^2 + 6abc

　3次の展開公式も，自然と覚えるまで演習問題を繰り返すのが良いでしょう．しかし，どうしても別の方法で覚えたい人のために，他の覚え方をいくつか紹介します．
　まずは，2次の展開公式と同様に，図で覚える方法を紹介します．2次の展開公式のコラムでも紹介しましたが，以下の記事でも同じことを書いています．

　まずは (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 を図で表してみます．

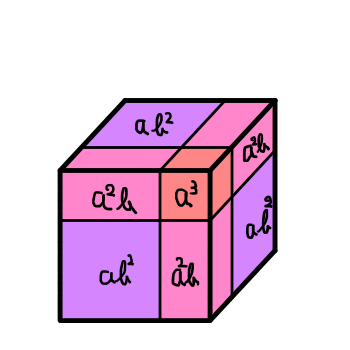
一辺 a + b の立方体の体積について考えます．体積を (a + b)^3 と表すことができますし，上の図から a^3 + 3a^2b + 3ab^2 + b^3 と表せることが分かります．3次になると，図が立体になり，見えない部分が出てくるのが厄介ですね． b^3 は完全に隠れてしまっています．

　次に (a - b)(a^2 + ab + b^2) = a^3 - b^3 を図で表してみましょう．動きが分かりづらいかと思います． (a - b)(a^2 + ab + b^2) = a^2(a - b) + ab(a - b) + b^2(a - b) であることを前提に以下の4つの図を見てみましょう．

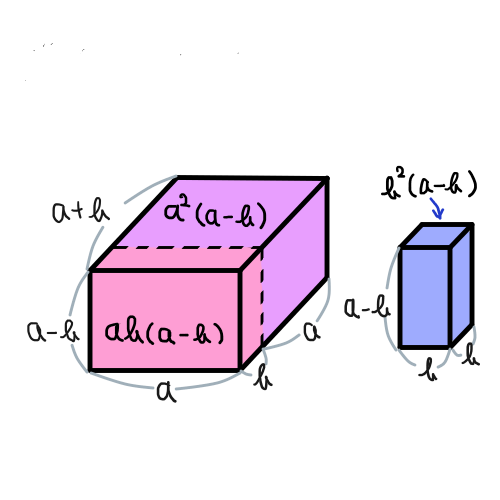
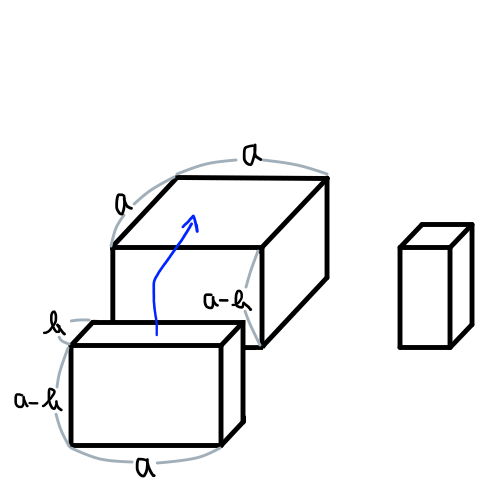
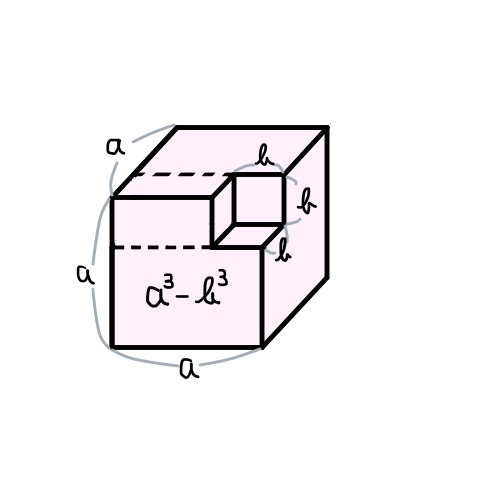
正直なところ，この図と動きを覚えるくらいなら，自然と覚えるまで演習問題を繰り返した方がいいと思います．

　動きが想像しにくい方は以下の記事もご参照ください．

　図では覚えられそうもない人は，次のコラムで解説する式や，二項定理を利用して覚えるのも良いでしょう．

　それでも1番良いのは，演習問題を解いているうちに自然と覚えることです．

　ちなみに (a + b + c)(a^2 + b^2 + c^2 - ab - bc - ca) = a^3 + b^3 + c^3 -3abc は，気合いで覚えましょう．次回に学習する因数分解で役立ちます．因数分解でも滅多に出てきませんが，公式なしで解くのは少し難しい⁷実は解法の流れが分かればそう難しいことではありませんが，ここでは難しいことにしておきます．ので，今のうちに覚えてしまうと楽かもしれません．

　4次以上の展開公式も存在しますが，あまり使うことはありません．しかし興味深い点も多いので，このコラムで紹介したいと思います．
　 (a + b)^n の展開公式や計算結果が a^n - b^n となる展開公式に関しては，一般化された式があります．

　まず，計算結果が a^n - b^n となる展開公式は，一般化すると以下のようになります．

この公式の n に様々な自然数を入れてみましょう．

n = 2 のとき
(a - b)(a + b) = a^2 - b^2

n = 3 のとき
(a - b)(a^2 + ab + b^2) = a^3 - b^3

n = 4 のとき
(a - b)(a^3 + a^2b + ab^2 + b^3) = a^4 - b^4

n = 5 のとき
(a - b)(a^4 + a^3b + a^2 b^2 + ab^3 + b^4) = a^5 - b^5

上記のように公式を導くことができます．また， n が奇数のときに， b に -b を代入すると別の公式になります．

n = 3 のとき
(a + b)(a^2 - ab + b^2) = a^3 + b^3

n = 5 のとき
(a + b)(a^4 - a^3b + a^2 b^2 - ab^3 + b^4) = a^5 + b^5

といった具合です．

　次に (a + b)^n の展開結果を一般化したいと思います． (a + b)^n の展開は二項定理⁸二項定理については後々のページで学習します．によって簡単に示せます．しかし，二項定理では未学習の記号を使う必要があるため，ここではパスカルの三角形を利用したいと思います．パスカルの三角形とは以下の図のような数字の並びです．

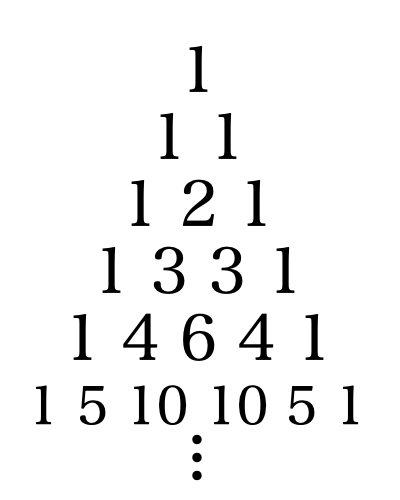
両端は常に 1 です．それ以外は，上の2つの数を足した数を，2つの数の下に書いています．

4段目右から2番目の 3 は，上にある 2 と 1 を足した数です．同様に5段目右から2番目の 4 は，上にある 3 と 1 を足した数になります．これがパスカルの三角形です．

　さて，(a + b)^n の n に 0 から順に自然数を入れて展開した結果を以下に示します．これとパスカルの三角形を見比べてみましょう．

(a + b)^0 = 1　⁹任意の数 a に対して a^0 = 1 が成り立ちます．
(a + b)^1 = a + b
(a + b)^2 = a^2 + 2ab + b^2
(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
(a + b)^5 = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5

展開後の各項の係数とパスカルの三角形の数字が一致しています．例えば，パスカルの三角形の6段目は 1, 5, 10, 10, 5, 1 で，(a + b)^5 の各項の係数 1, 5, 10, 10, 5, 1 と一致します．この一致を利用して，パスカルの三角形から (a + b)^n を求めることが可能です．

　余談になりますが，パスカルの三角形には面白い性質がたくさんあるため，遊び道具として適しています．本記事では性質に触れませんが，眺めていると面白い規則性がたくさん見つかります．ぜひ遊んでみてください．

例題5の解答と解説．
X = a + 2b とおきます． X とおいた式に，公式 (x + a)(x + b) = x^2 + (a + b)x + ab を使うと，
(X + 3c)(X - c) \\ = X^2 + 2cX - 3c^2
X に a + 2b を代入して，
X^2 + 2cX - 3c^2 \\ = (a + 2b)^2 + 2c(a + 2b) - 3c^2 \\ = a^2 + 4ab + 4b^2 + 2ca + 4bc - 3c^2 \\ = a^2 + 4b^2 - 3c^2 + 4ab + 4bc + 2ca

慣れてきたら， X とおかずに解くようにしましょう．

(a + 2b + 3c)(a + 2b - c) \\ = \{ (a + 2b) + 3c \} \{ (a + 2b) - c \} \\ = (a + 2b)^2 + (3c - c)(a + 2b) - 3c^2 \\ = a^2 + 4ab + 4b^2 + 2ca + 4bc - 3c^2 \\ = a^2 + 4b^2 - 3c^2 + 4ab + 4bc + 2ca

例題6の解答と解説．
(x^2 + y^2)(x + y)(x - y) \\ = (x^2 + y^2)(x^2 - y^2) \\ = x^4 - y^4

　(x^2 + y^2)(x^2 - y^2) に対して (a + b)(a - b) = a^2 - b^2 の公式を使いました．よく分からない人は，X = x^2 ，Y = y^2 とおくと理解しやすくなるかもしれません．

例題7の解答と解説．
(1)
(2x + y - 3z)(2x + y - z) \\ = \{ (2x + y) - 3z \} \{ (2x + y) - z \} \\ = (2x + y)^2 - 4z(2x + y) + 3z^2 \\ = 4x^2 + 4xy + y^2 - 8zx - 4yz - 3z^2 \\ = 4x^2 + y^2 - 3z^2 + 4xy - 4yz - 8zx

[別解]
X = 2x + y とおいて，
(X - 3z)(X - z) \\ = X^2 - 4zX + 3z^2
X に 2x + y を代入して，
X^2 - 4zX + 3z^2 \\ = (2x + y)^2 - 4z(2x + y) + 3z^2 \\ = 4x^2 + 4xy + y^2 - 8zx - 4yz - 3z^2 \\ = 4x^2 + y^2 - 3z^2 + 4xy - 4yz - 8zx


(2) (2a + b + c)(2a - 2b + c) \\ = \{ (2a + c) + b \} \{ (2a + c) - 2b \} \\ = (2a + c)^2 - b(2a + c) - 2b^2 \\ = 4a^2 + 4ca + c^2 - 2ab - bc - 2b^2 \\ = 4a^2 - 2b^2 + c^2 - 2ab - bc + 4ca

[別解]
X = 2a + c とおいて，
(X + b)(X - 2b) \\ = X^2 - bX - 2b^2
X に 2a + c を代入して，
X^2 - bX - 2b^2 \\ = (2a + c)^2 - b(2a + c) - 2b^2 \\ = 4a^2 + 4ca + c^2 - 2ab - bc - 2b^2 \\ = 4a^2 - 2b^2 + c^2 - 2ab - bc + 4ca


(3)
(9x^2 + 8y^2)(9x^2 - 8y^2) = 81x^4 - 64y^4

(4)
(7a^3 + 5b^3)(7a^3 - 5b^3) = 49a^6 - 25b^6

例題8の解答と解説．
\begin{aligned} x^2 + y^2 &= (x + y)^2 - 2xy \\ &= 4^2 - 2\times 3 \\ &= 16 - 6 \\ &= 10 \end{aligned}