楕円の方程式を求める 〜十分条件の証明付き〜
本記事では,楕円の方程式について解説します.
多くの参考書では,楕円の方程式を求める過程で両辺を2乗するため,必要条件しか証明されていないことがあります.本記事では,大雑把にではありますが,十分条件にも触れたい1すごく誤魔化しているので後日修正するかもしれません.と思います.
楕円の方程式
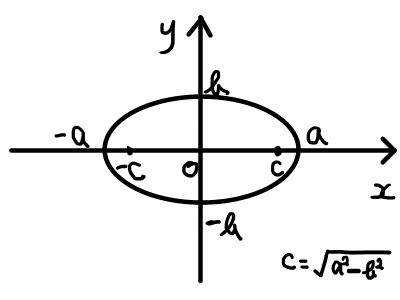
実数 a, b が 0<b<a を満たす定数のとき,以下の方程式は,中心が原点,焦点 (- \sqrt{a^2 - b^2} , 0), \,(\sqrt{a^2 - b^2} , 0) の楕円を表す.
\begin{aligned}
\frac{x^2}{a^2} + \frac{y^2}{b^2} &= 1 \\
\end{aligned}
また,楕円上の点と焦点の距離の和は 2a になる.
楕円の方程式の導出
楕円の方程式を求める方針を簡単に説明します.
楕円上の点と焦点の距離の和は 2a になるので,焦点の座標を (- c , 0), \,(c , 0) とおき,2つの焦点との距離の和が 2a となる点の軌跡を求めます.
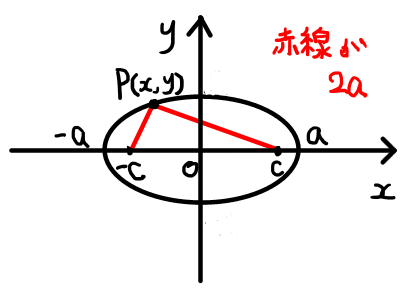
楕円上の点 \mathrm{P} の座標を (x,y) とすると,2つの焦点と点 \mathrm{P} との距離の和の間には以下の等式が成り立つ.
\begin{aligned}
\sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a \\
\sqrt{(x + c)^2 + y^2} = 2a - \sqrt{(x - c)^2 + y^2} \\
\end{aligned}
両辺を2乗して,
\begin{aligned}
(x + c)^2 + y^2 = 4a^2 - 4a\sqrt{(x - c)^2 + y^2} + (x - c)^2 + y^2 \\
\end{aligned}
\begin{aligned}
4a^2 - 4a\sqrt{(x - c)^2 + y^2} - 4cx &= 0 \\
a^2 - a\sqrt{(x - c)^2 + y^2} - cx &= 0 \\
a\sqrt{(x - c)^2 + y^2} &= a^2 - cx
\end{aligned}
両辺を2乗して,
\begin{aligned}
a^2 \{(x - c)^2 + y^2\} &= (a^2 - cx)^2 \\
a^2 x^2 - 2 a^2 c x + a^2 c^2 + a^2 y^2 &= a^4 -2 a^2 c x + c^2 x^2 \\
\end{aligned}
\begin{aligned}
(a^2 - c^2) x^2 + a^2 y^2 &= a^2 (a^2 - c^2) \\
\end{aligned}
両辺を a^2 (a^2 - c^2) で割ると,
\begin{aligned}
\frac{x^2}{a^2} + \frac{y^2}{a^2 - c^2} &= 1 \\
\end{aligned}
b^2 = a^2 - c^2 とおいて,
\begin{aligned}
\frac{x^2}{a^2} + \frac{y^2}{b^2} &= 1 \\
\end{aligned}
よって,楕円の方程式は, \begin{aligned} \frac{x^2}{a^2} + \frac{y^2}{b^2} &= 1 \end{aligned} となります.
また焦点の x 座標 c の値は,b^2 = a^2 - c^2 とおいたことから,c = \sqrt{a^2 - b^2}であることが分かります.
十分条件の確認
X = Y \Rightarrow X^2 = Y^2 は常に成り立ちますが,X^2 = Y^2 \Rightarrow X = Y は必ずしも成り立つとは限りません.
X = Y \Leftrightarrow X^2 = Y^2 が成り立つためには,X と Y が同符号である必要があります.
前節で楕円の方程式を導出しましたが,両辺を2乗する操作が2回ありました.
十分条件が成り立つことを示すために,方程式の導出過程を逆から見て,2乗する前の両辺が同符号であることを確認する必要があります.
2乗した式
\begin{aligned}
\sqrt{(x + c)^2 + y^2} &= \left\{ 2a - \sqrt{(x - c)^2 + y^2} \right\}^2 \\
(x + c)^2 + y^2 &= 4a^2 - 4a\sqrt{(x - c)^2 + y^2} + (x - c)^2 + y^2 \\
\end{aligned}
この式を2乗する前の式が両辺とも正であることを示します.
\begin{aligned}
\sqrt{(x + c)^2 + y^2} = 2a - \sqrt{(x - c)^2 + y^2}
\end{aligned}
左辺は焦点との距離であるため正,また a > 0 より,
\begin{aligned}
\sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a
\end{aligned}
\sqrt{(x + c)^2 + y^2} が正で,\sqrt{(x + c)^2 + y^2} も正なので,
2a - \sqrt{(x - c)^2 + y^2} も正である.

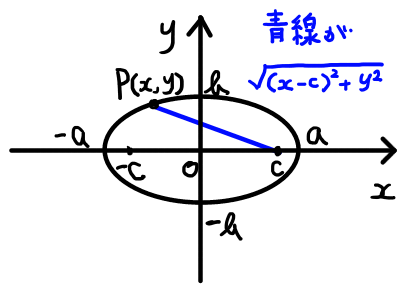
次に以下の等式が,両辺とも正であることも示します.
\begin{aligned}
a\sqrt{(x - c)^2 + y^2} &= a^2 - cx
\end{aligned}
a > 0 より,左辺は正.
0 < c < a であることと,x \leqq a より,右辺も正である.
楕円の形を示す指標(離心率,扁平率)
最後に,楕円が円からどれだけ離れた形をしているかを測る指標を2つ紹介します.
1つ目は離心率です.
離心率は焦点が中心からどれだけ離れているかを示します.0に近づくほど円に近づきます.
離心率 e は以下の式で求められます.
楕円の離心率.
\begin{aligned}
e = \frac{\sqrt{a^2 - b^2}}{a}
\end{aligned}
もう1つ紹介する指標は,扁平率です.
扁平率は0に近づくほど,円に近づきます.地学を学習した方は,回転楕円体としての地球において,馴染みのある指標かと思います.
扁平率 e は以下の式で求められます.
楕円の扁平率.
\begin{aligned}
f = \frac{a - b}{a} = 1 - \frac{b}{a}
\end{aligned}

