様々な開平法 〜平方根の近似値の求め方〜
みなさんは\sqrt{2}などの平方根の値が,どのように求められているか疑問に思ったことはありませんか?平方根の近似値1おおよその値,近い値のこと.を求める手法は色々あります.
この記事では,4つの手法を紹介し,それぞれの手法で\sqrt{2}の近似値を求めてみたいと思います.2つ目以降の手法は高校で習う内容ではありませんが,参考書のコラムなどに掲載されることもありますので,高校生でも十分理解可能な難易度です.
地道に求める
\sqrt{2}を地道に求めます.
2乗して2を超えない最大の数を1桁ずつ見つけましょう.
まずは一の位から.
0^2 = 0 < 2
1^2 = 1 < 2
2^2 = 4 > 2
一の位は1のようです.
次に,小数第一位の値を探します.
1.0^2 = 1 < 2
1.1^2 = 1.21 < 2
1.2^2 = 1.44 < 2
1.3^2 = 1.69 < 2
1.4^2 = 1.96 < 2
1.5^2 = 2.25 > 2
小数第一位は4です.
次に,小数第二位の値を探します.
1.40^2 = 1.96 < 2
1.41^2 = 1.9881 < 2
1.42^2 = 2.0164 > 2
小数第二位は1です.
次に,小数第三位の値を探します.
1.410^2 = 1.9881 < 2
1.411^2 = 1.990921 < 2
1.412^2 = 1.993744 < 2
1.413^2 = 1.996569 < 2
1.414^2 = 1.999396 < 2
1.415^2 = 2.002225 > 2
小数第三位は4です.
次は,小数第四位.
1.4140^2 = 1.999396 < 2
1.4141^2 = 1.99967881 < 2
1.4142^2 = 1.99996164 < 2
1.4143^2 = 2.00024449 > 2
小数第四位は2です.
次.
1.41420^2 = 1.99996164 < 2
1.41421^2 = 1.9999899241 < 2
1.41422^2 = 2.0000182084 > 2
小数第五位は1です.
……
1.414210^2 = 1.9999899241 < 2
1.414211^2 = 1.999992752521 < 2
1.414212^2 = 1.999995580944 < 2
1.414213^2 = 1.999998409369 < 2
1.414214^2 = 2.000001237796 > 2
3
1.4142130^2 = 1.999998409369 < 2
1.4142131^2 = 1.99999869221161 < 2
1.4142132^2 = 1.99999897505424 < 2
1.4142133^2 = 1.99999925789689 < 2
1.4142134^2 = 1.99999954073956 < 2
1.4142135^2 = 1.99999982358225 < 2
1.4142136^2 = 2.00000010642496 > 2
5
1.41421350^2 = 1.99999982358225 < 2
……
……
……
狂いそうぅぅ!
筆算による開平計算
次に,筆算による開平計算について説明します.
突然ですが,筆算の手順から見ていきましょう!ここでは,\sqrt{67.7329}を例にして,筆算の手順を説明します.
手順1.
小数点を中心に2桁ずつ区切ります.

手順2.
1番左のブロックに注目します.そのブロックの数字を超えない最大の平方数を見つけます.今回は8^2 = 64が条件を満たします.もとの数を左側に2つ,ブロックの上に1つ書きます.また,平方数をブロックの下に書きます.
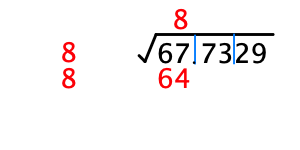
手順3.
横線を引いて次のステップへ移る準備をします.左側の2つの数字を足したものを線の下に書きましょう.ここでは8+8=16で16と書きます.次に着目しているブロックの数から,その下に書いてある数を引きます(67-64=3).最後に,次のブロックの数字を降ろしてきます.次のブロックがなく,また,引き算の結果が0でない場合は,0を2つ降ろしましょう.

手順4.
左の数をmとします.(m \times 10 + n) \times nのうち,真ん中の数字(373)を超えない最大のnを見つけ,計算結果を真ん中に書きます(今回は162×2=324).そのnをmの横にひとつ,その下にひとつ,現在のブロックの上にひとつ書きます.

手順5.
手順3と手順4を繰り返します.ブロックが全て無くなったうえで,引き算の結果が0になれば終了です.無限に続く場合は,気が済むまで計算しましょう.
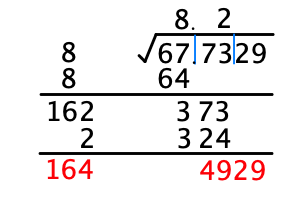

さて,筆算による開平計算ですが,この計算方法は以下の式が成り立つことを利用しています.
(a_{1} + a_{2} + a_{3} + a_{4} + \cdots)^2
= a_{1}^2
+ a_{2}(2a_{1} +a_{2})
+ a_{3} \{2(a_{1} + a_{2}) + a_{3}\}
+ a_{4} \{2(a_{1} + a_{2} + a_{3}) + a_{4}\}
+ \cdots \cdots
このことを,先ほどの\sqrt{67.7329}を例にして確認してみましょう.
イメージとしては,面積が67.7329である正方形の,一辺の長さを求めていると考えます.

先ほどの式に今回の例を当てはめると以下のようになります.
67.7329
=(8 + 0.2 + 0.03)^2
=8^2
+0.2(2 \cdot 8 + 0.2)
+0.03\{ 2( 8 + 0.2) + 0.03 \}
下の図と上の式を見比べてください.8^2が赤い部分,0.2(2 \cdot 8 + 0.2)が緑の部分,0.03\{ 2( 8 + 0.2) + 0.03 \}が青い部分に当たります.

また,それぞれの式を計算してみます.
8^2=64
0.2(2 \cdot 8 + 0.2) = 3.24
0.03\{ 2( 8 + 0.2) + 0.03 \} = 0.4929
ここまでの式や数字と,筆算で書いた数字を見比べることで,筆算で何をしていたかが分かると思います.ざっくりと説明しますと,上の図の,赤い部分,緑の部分,青い部分の面積を順に求めながら,同時に該当部分に対応する長さも求めていたわけです.
それでは,筆算で\sqrt{2}の近似値を計算してみましょう.

参考過去記事:開平法の筆算(√8まで)
頭がおかしくなりそう……
手計算がものすごく大変なので,筆算の過程を表示するプログラムを作成しました.
連分数を利用する
次に,連分数を利用して\sqrt{2}の近似値を求めます.
(\sqrt{2}+1)(\sqrt{2}-1)=1より
\sqrt{2}-1=\frac{1}{\sqrt{2}+1}
\sqrt{2} = 1 + \frac{1}{1 + \sqrt{2}}
右辺の\sqrt{2}にこの式自体を代入して
\sqrt{2} = 1 + \frac{1}{1 + 1 + \frac{1}{1 + \sqrt{2}}}
この操作を好きなだけ繰り返して,最後に残った\sqrt{2}を1とみなして計算を行えば,\sqrt{2}の近似値を求めることができます.
ちなみに,\frac{1}{1 + 1 + \frac{1}{1 + \sqrt{2}}}のような分母に分数がある形の分数を連分数と呼びます.
この節の最後に,連分数を用いて\sqrt{2}の近似値を計算してみます.
1 + \frac{1}{1 + 1} = \frac{3}{2} = 1.5
1 + \frac{1}{2 + \frac{1}{1 + 1}} = \frac{7}{5} = 1.4
1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{1+1}}} = \frac{17}{12} = 1.41666 \cdots
ニュートン法を用いる
この手法の理解には「微分」の知識が必要です.
ニュートン法とは,関数f(x)に関して,f(x)=0となるxの近似値を求めるアルゴリズム2アルゴリズムがよく分からない人は,手順とか手法だと思ってください.です.
手順は簡単で,テキトーな初期値x_{0}を用意し,以下の漸化式によって近似値を求めます.
x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}ここではf(x)=0の解に\sqrt{2}が含まれるようなf(x)として,f(x)= x^2 - 2を用意します.
初期値をx_{0}=4とすると,
x_{0}=4
x_{1}=2.25
x_{2}=1.5694444444444444
x_{3}=1.4218903638151426
x_{4}=1.4142342859400734
x_{5}=1.4142135625249321
x_{6}=1.4142135623730951
x_{7}=1.414213562373095
といったように\sqrt{2}の値に近づいていきます.
さて,ここでニュートン法では何をしているのか考えてみましょう.そのために,以下の式の出自について考えます.
x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}まずは,xy平面で点(a, b)を通り,傾きがmの直線を考えてみましょう.
その直線は方程式
y-b = m(x-a)
で表されます3傾きがmの直線の方程式はy=mx+\alpha
そこにx=a,y=bを代入して,
b = ma + \alpha
\alpha = b - ma
\alphaをもとの式に代入して,
y = mx + b - ma
y-b = m(x-a).
点(x_{n}, f(x_{n}))におけるf(x)の接線は,傾きがf'(x_{n})なので,
y- f(x_{n}) = f'(x_{n})(x-x_{n})
y=0のときのxをx_{n+1}とすると,
- f(x_{n}) = f'(x_{n})(x_{n+1}-x_{n})
整理して
x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}となります.
点(x_{n}, f(x_{n}))における接線とx軸の交点のx座標をx_{n+1}にしていたんですね.
ちなみに,近似の過程を可視化すると以下のようになります.
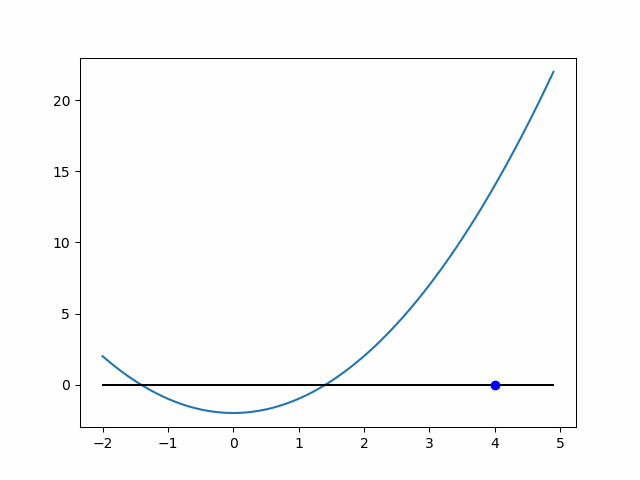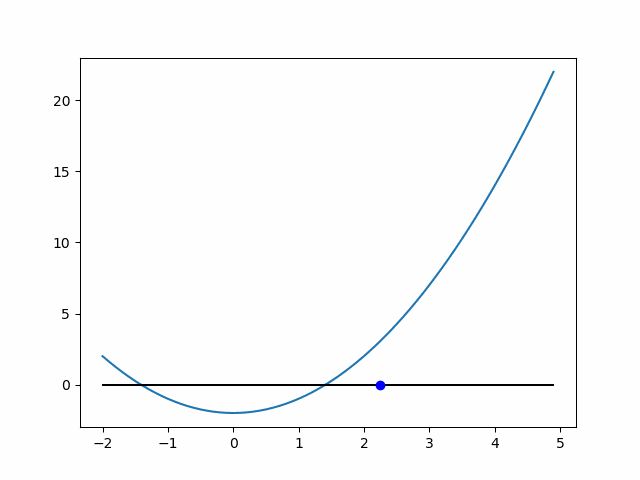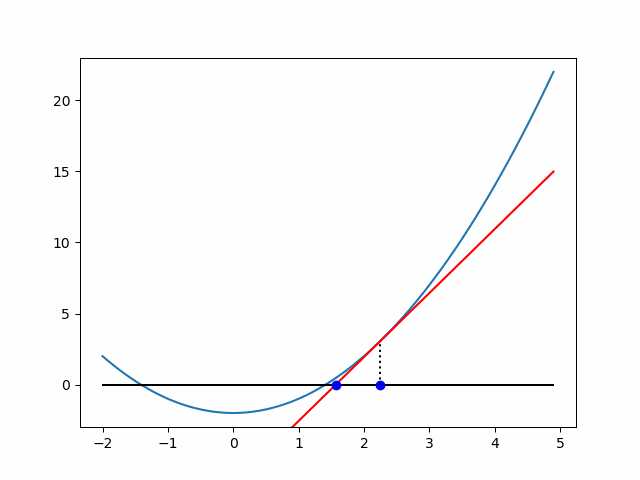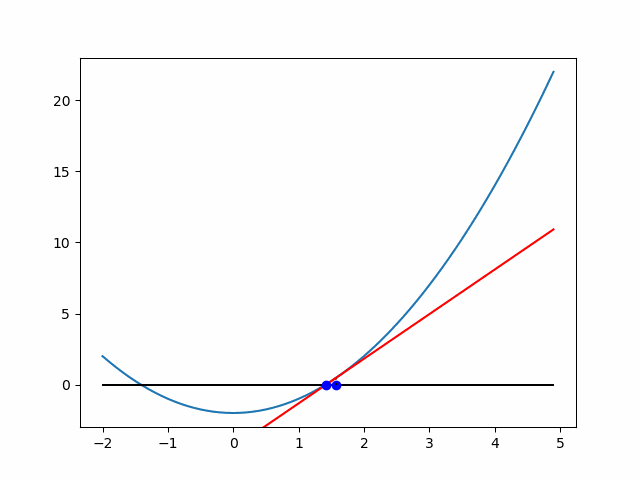
参考過去記事:ニュートン法による√2の近似過程の可視化
参考過去記事にgifアニメを作成したPythonのコードを載せています.
まとめ
平方根の近似値を求める4つの手法を紹介しましたが,いかがだったでしょうか4「平方根を求める」というひとつの問題に対して,さまざまなアプローチがあります.数学の問題には様々な解決方法があると実感する一助になっていれば,幸いです.(本文中に書くと説教臭くなるので,注釈に書いてみました)?
最後に,4つの手法を全て試した私から,皆さんに一言だけ伝えさせてください.
「手計算は辞めておけ.正確な値が欲しいときは,特に.」

