点の平行移動とグラフの平行移動
平面上(xy直交座標)の点(x,y)をx軸方向へ1,y軸方向へ2平行移動させると,点(x+1,y+2)となります.一方,平面上の関数y=f(x)のグラフをx軸方向へ1,y軸方向へ2平行移動させると,関数y-2=f(x-1) となります.
点の平行移動の場合は移動した量を足していますが,関数の平行移動の場合は引いています.この違いは,なぜ生じるのでしょうか?
といったことを,冗談半分で聞いてみたのですが,本当に「なんで?」となった人は,この記事を読んで,しっかりと復習しましょう.
グラフ上の対応する点について考えます.元のグラフのある点を(x,y),x軸方向へ1,y軸方向へ2平行移動させたグラフ上の対応する点を(x',y')とします.
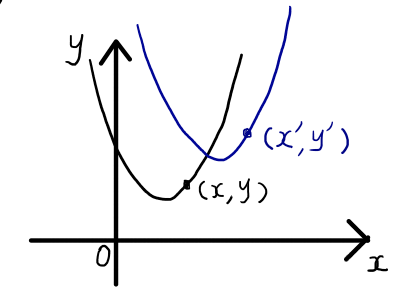
すると,(x',y')と(x,y)の関係は以下の式で表されます.
x' = x + 1 \\ y' = y + 2
さて,y = f(x)を平行移動した関数に変換することが目的ですから,
x = x' - 1 \\ y = y' - 2
これをy = f(x)に代入した,y'-2 = f(x'-1)が求めたい関数となります.
このように,代数的に計算してしまえば納得できるかと思います.
どうしても他の解釈をつけたい場合は,視点の違いなどはいかがでしょうか.点の平行移動について考えているときは,元の点から移動後の点を見ている,関数の平行移動のときは,移動後の関数から元の関数を見ている,と少しモヤモヤしますがこんな感じです.
また,関数を2次関数に限定する場合,基本形について頂点の座標を考えることも有効です.
\begin{aligned}
y &= (x-p)^2 + q \\
y - q &= (x-p)^2
\end{aligned}頂点の座標をx軸方向へ1,y軸方向へ2平行移動させると,
\begin{aligned}
y - (q + 2) &= \{x-(p + 1)\}^2 \\
y - q - 2 &= (x - p - 1)^2 \\
(y-2) -q &= \{(x-1) -p\}^2
\end{aligned}となります.

