直線の方程式 〜点と直線の距離〜
この記事ではxy座標上の,点と直線の距離を求めます.
距離を計算する式を求める方法は,大きく分けて3通りあります.点からの垂線と直線の交点の座標を利用する方法,三角形を利用する方法,ベクトルを使う方法です.
この記事では,前者2つを紹介します.「ベクトル」は令和4年度開始の学習指導要領では,数学Cに位置付けられていますから,学習済みの方のための演習問題に留めたいと思います.
ちなみに,最も直感的に分かりやすい方法も,計算が簡単な方法も,ベクトルを用いる手法です.なぜベクトルを数学Cにしたのでしょう?1シュワルツの不等式といい,ベクトルを知らないと暗記に頼りがちになると思うのですが,文科省は文系学生に数学の暗記科目化を勧めているのでしょうか?
命題
点と直線の距離.
点(x_1, y_1)と直線ax + by + c = 0の距離は,
\begin{aligned}
\frac{|ax_1 + by_1+ c|}{\sqrt{a^2 + b^2}}
\end{aligned}
証明1.
点(x_1, y_1)からax + by + c = 0へ垂線を降ろし,その交点を(x_2, y_2)
(x_2, y_2)は,直線ax + by + c = 0と垂線b(x - x_1) -a(y - y_1) = 0の上にあるので,
a(x_2 - x_1) + b(y_2 - y_1) + ax_1 + by_1 + c = 0
b(x_2 - x_1) -a(y_2 - y_1) = 0
この2つの式を同時に満たす.
ここでX = x_2 - x_1,Y = y_2 - y_1とおく2x_2 - x_1,y_2 - y_1の方が何をしているのかが分かりやすいですが,表示の都合上このようにおいています..
aX + bY + ax_1 + by_1 + c = 0
bX -aY = 0
これを解いて,
\begin{aligned}
X &= \frac{-b(ax_1 + by_1+ c)}{a^2 + b^2} \\
Y &= \frac{a(ax_1 + by_1+ c)}{a^2 + b^2}
\end{aligned}
\begin{aligned}
X^2 = \frac{b^2(ax_1 + by_1+ c)^2}{(a^2 + b^2)^2} \\
Y^2 = \frac{a^2(ax_1 + by_1+ c)^2}{(a^2 + b^2)^2}
\end{aligned}
\begin{aligned}
\sqrt{X^2 + Y^2} &= \sqrt{ \frac{(a^2 + b^2)(ax_1 + by_1+ c)^2}{(a^2 + b^2)^2}} \\
&= \frac{\sqrt{(ax_1 + by_1+ c)^2}}{\sqrt{(a^2 + b^2)}} \\
&= \frac{|ax_1 + by_1+ c|}{\sqrt{a^2 + b^2}}
\end{aligned}
証明2.
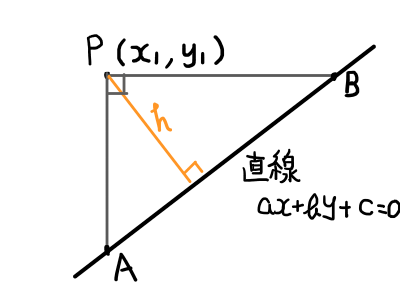
点(x_1, y_1)を点\mathrm{P}とする.
点Pから直線ax + by + c = 0に向かって,x軸,y軸に平行な2本の直線を伸ばす.点Pを通るy軸に平行な直線と,直線ax + by + c = 0の交点を\mathrm{A} = (x_a, y_a)とする.点Pを通るx軸に平行な直線と,直線ax + by + c = 0の交点を\mathrm{B} = (x_b, y_b)とする.
また,求めたい距離をhとする.
ここで\bigtriangleup \mathrm{PAB}の面積Sを求める.
\angle \mathrm{APB} = 90^{\circ}なので,
\begin{aligned}
S &= \frac{1}{2} \mathrm{PA} \cdot \mathrm{PB} \\
&= \frac{1}{2} |y_1 - y_a| |x_1 - x_b|
\end{aligned}
一方でS = \frac{1}{2} h \mathrm{AB}なので,
\begin{aligned}
S &= \frac{1}{2} h \mathrm{AB} \\
&= \frac{1}{2} h \sqrt{(x_a - x_b)^2 + (y_a - y_b)^2}
\end{aligned}
2つの式を合わせて,
\begin{aligned}
h &= \frac{|y_1 - y_a| |x_1 - x_b|}{\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2}}
\end{aligned}
x_a = x_1,y_b = y_1なので,
\begin{aligned}
h &= \frac{|y_1 - y_a| |x_1 - x_b|}{\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2}} \\
&= \frac{|y_1 - y_a| |x_1 - x_b|}{\sqrt{(x_1 - x_b)^2 + (y_a - y_1)^2}} \\
&= \frac{|x_1 - x_b| |y_1 - y_a|}{\sqrt{(x_1 - x_b)^2 + (y_1 - y_a)^2}} \\
&= \frac{|b| |x_1 - x_b| |y_1 - y_a|}{|b| \sqrt{(x_1 - x_b)^2 + (y_1 - y_a)^2}} \\
&= \frac{|x_1 - x_b| |by_1 - by_a|}{\sqrt{b^2(x_1 - x_b)^2 + (by_1 - by_a)^2}} \\
\end{aligned}
点\mathrm{A} = (x_1, y_a)と点\mathrm{B} = (x_b, y_1)は直線ax + by + c = 0上にあるので,
\begin{aligned}
& ax_1 + by_a + c = 0 \\
&\Leftrightarrow by_a = -ax_1 - c \cdots (1)
\end{aligned}
\begin{aligned}
& ax_b + by_1 + c = 0 \\
&\Leftrightarrow by_1 = -ax_b - c \cdots (2)
\end{aligned}
(2) - (1)より
by_1 - by_a = ax_1 - ax_b
また,ax_b = -by_1 - cより,
by_1 - by_a = ax_1 + by_1 + c
これらを代入して,
\begin{aligned}
h &= \frac{|x_1 - x_b| |by_1 - by_a|}{\sqrt{b^2(x_1 - x_b)^2 + (by_1 - by_a)^2}} \\
&= \frac{|x_1 - x_b| |ax_1 + by_1 + c|}{\sqrt{b^2(x_1 - x_b)^2 + (ax_1 - ax_b)^2}} \\
&= \frac{|x_1 - x_b| |ax_1 + by_1 + c|}{\sqrt{(a^2 + b^2)(x_1 - x_b)^2}} \\
&= \frac{|x_1 - x_b| |ax_1 + by_1 + c|}{ |x_1 - x_b| \sqrt{a^2 + b^2}} \\
&= \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}} \\
\end{aligned}
演習問題
演習.
点と直線の距離をベクトルを用いて求めましょう.

