2点間の距離 〜ユークリッド距離,マンハッタン距離,距離の公理〜
2点間の距離について解説します.
※注意
中盤以降は高校の学習指導要領外の内容です.
平面上の2点間の距離(高校で習う距離)
xy平面上の2点の距離は以下のように定義されます.
定義.
xy平面上の2点(x_1 , y_1) ,(x_2 , y_2) の距離は,
\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
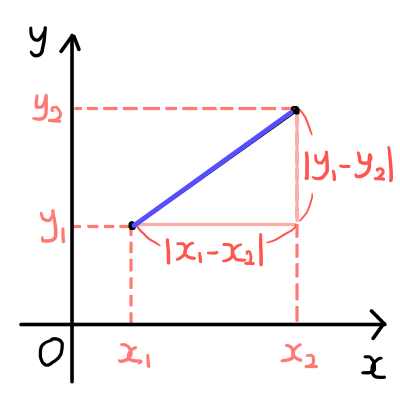
イメージとしては,直線距離でしょうか.2点間の線分の長さというイメージでもいいと思います.
空間上の2点間の距離
xyz空間上の2点の距離は以下のように定義されます.
定義.
xyz空間上の2点(x_1 , y_1, z_1) ,(x_2 , y_2, z_2) の距離は,
\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 }
距離ってこれしかないの?
※これ以降は高校の学習指導要領外の内容です.
さて数学における距離とは,高校で習うこの距離だけでしょうか?
現実世界には,直線距離以外の距離もあります.
タクシーに乗ったときに「ここから東京タワーまでの距離はどれくらいですか?」と訊いて,直線距離を答えられたら,あなたは怒るでしょう.この場合は,道沿いの距離が返ってくることを要求しているはずです.
それでは,数学における他の距離のうち,有名なものをひとつ紹介したいと思います.
マンハッタン距離
高校で習う先述の距離のことを,ユークリッド距離といいます.
他の有名な距離として,マンハッタン距離があります.マンハッタン距離の定義は以下の通りです.
マンハッタン距離の定義.
平面の場合:
|x_1 - x_2| + |y_1 - y_2|
空間の場合:
|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|
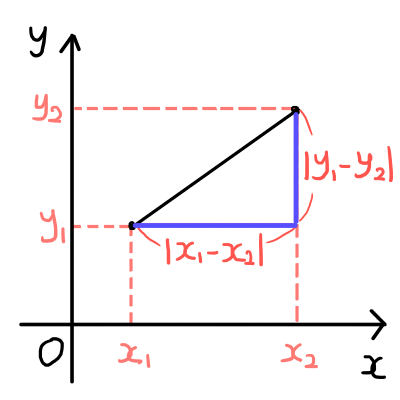
上の図においては,青い部分の長さの合計がマンハッタン距離となります.
マンハッタン距離のイメージは,座標軸に平行に進んだ最短の道のりです.
ちなみに名前の由来は,マンハッタンの道が碁盤目状になっており,マンハッタンを道沿いに進むことが,座標軸に対して平行に進むことに似ていることから来ています1京都の方が綺麗な碁盤目状なので,京都距離と呼んでも良いのでは?.
距離の公理
ちなみに距離の公理を満たしているものは,なんでも距離となります.
距離の公理.
集合Xの任意の要素 a,b,c に関して,2変数関数 d が以下の条件を満たすとき,d のことを距離,または距離関数といいます.
d(a, b) = 0 \Leftrightarrow a = b
d(a, b) = d(b, a)
d(a, b) + d(b, c) \geqq d(a,c)
さて,ここで重要なことは,集合の要素が座標上の点である必要がないということです.
次回の記事では,文字列や木構造といった離散構造の距離について解説します.
もちろん,高校の学習指導要領の内容ではありません.
(2023年3月20日追記)
文字列(配列)の距離の解説記事が出来ました!