3次の展開公式の図を動かしてみた

以前，展開公式(乗法公式)を図で表す記事を書きました．

展開公式を図示する

この記事では，(a+b)^3 = a^3 +3a^2b + 3ab^2 +b^3や(a - b)(a^2 + ab + b^2) = a^3 - b^3の図が少し分かりにくい状態でした．

本記事では，Blenderなどのソフトを使い，3次の展開公式の図を動かしてみたいと思います．

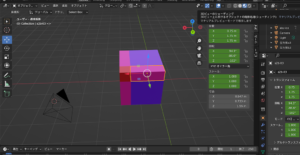
(a+b)^3 = a^3 +3a^2b + 3ab^2 +b^3

文字送りが少し早いため辺の長さの把握が大変ですが，分かりやすくなった気がします．

(a - b)(a^2 + ab + b^2) = a^3 - b^3

次は(a - b)(a^2 + ab + b^2) = a^3 - b^3を動かします．以前の記事では(a - b)(a^2 + ab + b^2)からa^3 - b^3へと動かしていましたが，今回は，a^3 - b^3から(a - b)(a^2 + ab + b^2)へと変形させます．

何だかパズルみたいになっています．辺の長さの把握が難しくなりましたが，動きは動画の方がわかりやすいですね．

まとめ

図と比べて少しは分かりやすくなったでしょうか．
個人的には，動きはわかりやすいですが，辺の把握が難しくなったので，無理に動かさなくても良いような気がしています．

ちなみに，今回作成したアニメーションといくつかの図を一本の動画にまとめました．

（2022年3月25日追記）
メイキング記事を作成しました．

メイキング 〜展開公式のアニメーション〜

　　

「勝手気ままに高校数学」シリーズ一覧へ