平方根の解説
無理数1英語でirrational number(直訳で「比で表せない数」)とは,分数で表せない数のことです2この定義には穴があるのですが,気になる方はこちら.無理数の例として円周率の\piや正の平方根の\sqrt{2},\sqrt{3}などが挙げられます.
この記事では,平方根について解説したいと思います.
平方根とは
nの平方根とは,2乗するとnになる数のことです.例えば,4の平方根は2と-2,9の平方根は3と-3となります.実数の場合,n=0の場合を除いて,必ずmと-mが平方根になる,つまり,絶対値が等しい2つの実数が平方根となります.
正の平方根
\sqrt{n}は,正の平方根です.文脈によっては「正の」が省略されることがあります.また,記号√のことを根号といいます.
正の平方根の代表例である\sqrt{2}は,簡単に発見することができます.
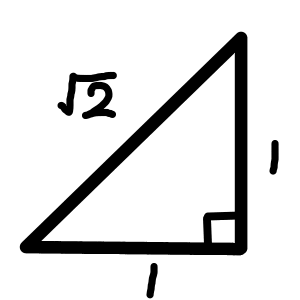
2辺の長さが1の直角二等辺三角形について考えると,三平方の定理より,その斜辺が\sqrt{1^2 + 1^2} = \sqrt{2}であることが分かります.
ここからは余談になります.
先ほどの直角二等辺三角形の斜辺が分数で表せないことは,ギリシャでは紀元前から知られていました.
紀元前6世紀に,ピタゴラスは「世界のすべては数学で説明できる」との信念のもと,教団を作っていました.しかし,その数の体系は整数を中心としたものであり,整数の比で表される有理数は認められていましたが,そこには無理数がありませんでした.ピタゴラス学派の人々は,直角二等辺三角形の斜辺を分数で表せないことに気づき始め,そのことがピタゴラス学派の没落に繋がったという説があります.
一方で,三平方の定理は「ピタゴラスの定理」とも呼ばれます3海外ではこちらの呼び方が主流.自分の名前のついた定理が,自分の教団の行き詰まりと密接な関係にある,これはなかなか皮肉なものです.
余談終わり.
ちなみに,正の平方根の値や,値の求め方に興味のある方は,以下の記事を参考にしてみてください.
正の平方根の性質
平方根の性質を4つ示します.
(1)
\sqrt{a^2} = |a|
a \geqq 0 のとき \sqrt{a^2} = a
a < 0 のとき \sqrt{a^2} = -a
(2)
\sqrt{a}\sqrt{b} = \sqrt{ab} (a > 0, b>0)
(証明)
両辺を2乗して(両辺が正より,両辺を2乗しても等号が成り立つ)
\begin{aligned}
(左辺)^2 &= (\sqrt{a}\sqrt{b})^2 \\
&= ab \\
&= \sqrt{ab} \\
&= (右辺)^2
\end{aligned}
(3)
\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} (a > 0, b>0)
(証明)
(2)と同様に証明できます.
(4)
\sqrt{c^2a}=c \sqrt{a} (a > 0, c>0)
(証明)
(2)を使って証明できます.
分母の有理化
分数の分母に根号があるときに,分母から根号が無くなるように式を変形することを,分母の有理化,もしくは,単に有理化といいます.分母と分子に同じ数をかけても,元の数と変わらない性質を利用します.通分や約分と同じ要領です.
まずは分母に根号が1つだけの場合を見てみましょう.(\sqrt{a})^2 = a を使います.
\frac{\sqrt{3}}{\sqrt{2}} = \frac{\sqrt{3} \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{6}}{2}次に,分母の根号が2つの場合を見てみましょう.今度は,(a+b)(a-b)=a^2 -b^2 を利用します.
\begin{aligned}
\frac{1}{\sqrt{3} + \sqrt{2}} &= \frac{(\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2})(\sqrt{3} - \sqrt{2})} \\
&= \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^2 - (\sqrt{2})^2} \\
&= \sqrt{3} - \sqrt{2}
\end{aligned}分母に根号が3つ以上ある場合は,2つや1つの時と同様の手順で有理化します.
\begin{aligned}
\frac{1}{\sqrt{2} + \sqrt{3} + \sqrt{5}} &= \frac{\sqrt{2} + \sqrt{3} - \sqrt{5}}{\{(\sqrt{2} + \sqrt{3}) + \sqrt{5}\} \{(\sqrt{2} + \sqrt{3}) - \sqrt{5}\}} \\
&= \frac{\sqrt{2} + \sqrt{3} - \sqrt{5}}{(\sqrt{2} + \sqrt{3})^2 - (\sqrt{5})^2} \\
&= \frac{\sqrt{2} + \sqrt{3} - \sqrt{5}}{2\sqrt{6}} \\
&= \frac{\sqrt{6}(\sqrt{2} + \sqrt{3} - \sqrt{5})}{2(\sqrt{6})^2} \\
&= \frac{3\sqrt{2} + 2\sqrt{3} - \sqrt{30}}{12}
\end{aligned}2重根号の外し方
\sqrt{p + 2\sqrt{q}}のように,根号の中に根号がある状態を2重根号といいます.
ここでは2重根号の外し方を解説します.
まずは,何とかしてこの形\sqrt{p + 2\sqrt{q}}にしましょう.中にある2がポイントです.
2重根号が外れた状態を\sqrt{a} + \sqrt{b}とすると,
\sqrt{p + 2\sqrt{q}}=\sqrt{a} + \sqrt{b}となる,a,bを探せば良いことが分かります.
両辺が正より,両辺を2乗して,
p + 2\sqrt{q}=(a + b) + 2\sqrt{ab}
つまり,a + b = p,ab = qとなるa,bを探せば良いことが分かります.因数分解のたすき掛けと似ていますね.
試しに\sqrt{5 + 2\sqrt{6}}の2重根号を外してみましょう.
\begin{aligned}
\sqrt{5 + 2\sqrt{6}} &= \sqrt{2+3 + 2\sqrt{2\cdot 3}} \\
&= \sqrt{(\sqrt{3} + \sqrt{2})^2} \\
&= \sqrt{3} + \sqrt{2}
\end{aligned}
\sqrt{p - 2\sqrt{q}}の場合は,同様にして,
2重根号が外れた状態を\sqrt{a} - \sqrt{b} (a>b>0)とすると,
\sqrt{p - 2\sqrt{q}}=\sqrt{a} - \sqrt{b}となる,a,bを探します.
両辺が正より,両辺を2乗して,
p + 2\sqrt{q}=(a + b) - 2\sqrt{ab}
同様に,a + b = p,ab = qとなるa,bを探せば良いことが分かります.ただし,a>b>0となる点は要注意です.
最後に,2重根号の外し方は,先の単元の,ちょうど忘れそうな頃に必要となります4三角比の単元で\sin 15^{\circ}や\cos 15^{\circ}を求めるとき等で必要..是非マスターしておきましょう.
