2次関数の基礎
2次関数について基礎から解説します.
関数とは何か
そもそも関数とは何でしょうか.関数とは,変数の値をひとつ決めると,それに対応する値がひとつ決まる,そのような対応関係のことです.何かをひとつ入力してやると,何かがひとつ出力されるブラックボックスだと考えていただければ良いでしょう.ひとつの入力に対して,ふたつもみっつも出力されることはありません1プログラミングの関数だといくらでも返ってくるけれど..同じ入力に対しては,必ず同じ出力が返ってきます.
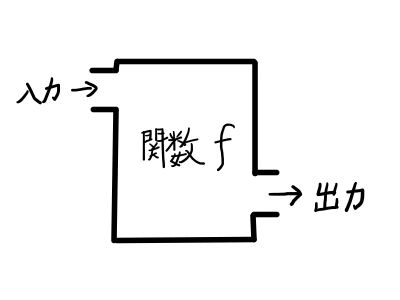
高校数学では基本的に,ひとつの数を決めると,対応するひとつの数が定まる1変数関数しか取り扱いません2大学では,いくつかの数の組を入力したり(多変数関数),ベクトルを入力したり,集合を入力したりします.楽しい..
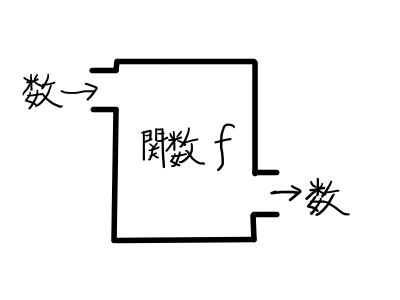
ちなみに,「関数」は昔は「函数」と書かれていました.このことに関して,森毅先生の『現代の古典解析』に面白い注釈がありますので,引用させていただきます.
昔は函数と書いたのが,最近は関数と書くようになったが,ハコだから昔に帰れ,という説がある.それも凾数がよいという.入力が口にあるが,出力がどこかというと,それは又(マタ)の間さ,という人体のブラック・ボックスのオソマツ.
森毅『現代の古典解析』ちくま学芸文庫(2006)190頁.
私は,函数が良いと思います.又(マタ)からは2種類のモノが出てきますから,という野暮なツッコミ.
閑話休題.
1次関数を使って,関数に慣れていきましょう.xを変数とするとき,1次関数f3function(関数)の頭文字fがよく使われます.は次のような形をしています.
f(x) = ax+b (a,bは定数,a \neq 0)
f(x)は関数fに変数xを入力したときの値を表しています.
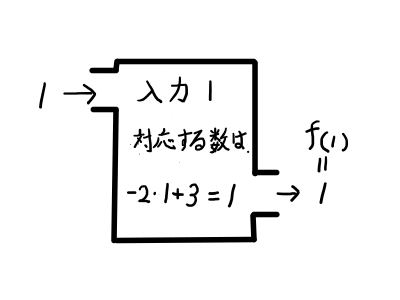
「ハコ」のイメージでいきますと,xを入力するとf(x)が出力されるということです.
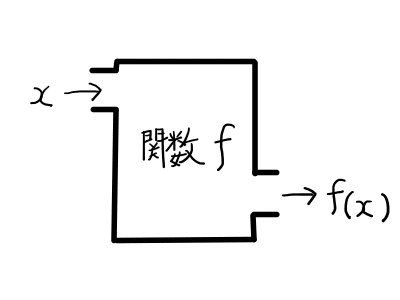
1次関数の場合,xをひとつ定めるとax+bがただひとつ定まります.
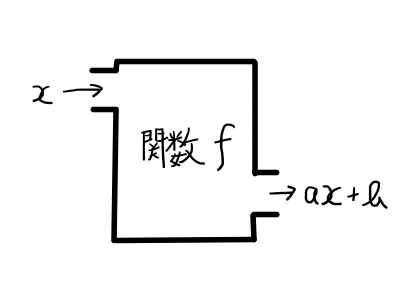
f(x)の代わりにyを用いて,y=ax+bと書き,yはxの関数であるということがあります.しかし,f(x)と書くと便利な場合も多いので,この書き方にも慣れておきましょう.
f(x)では括弧の中に変数xを入れているため値が定まりませんが,定数を入れてやると値がひとつに定まります.関数f(x)についてx=a (aは定数)のとき,対応する値のことをf(a)と表すことができます.
慣れるために,以下の1次関数について考えてみましょう.
f(x) = -2x+3
さて,この関数についてx=1のとき,f(1) = -2 \cdot 1 + 3 = 1と書き表すことができます.
f(1) = 1と書くけば,変数の値を1で定めると,対応する値が1となることがすぐに分かります.
演習.
上記の関数f(x) = -2 x + 3 について,次の値を求めなさい.
f(-1) f(4) f(\frac{3}{2})
2次関数の基本
2次関数は読んで字のごとく,次数が2次の関数のことです4次数が分からない人はこちらへ..一般的な形は以下のようになります.
f(x) = ax^2+bx+c (a,b,cは定数,a \neq0)
xをひとつ決めると,xに対応した値,ax^2+bx+cがただひとつ定まるということです.対応する数をyとすると,以下のようにも書けます.
y = ax^2+bx+c (a,b,cは定数,a \neq0)
このような形式を2次関数の一般形といいます.
2次関数のグラフ
初めて出会った種類の関数は,グラフに描いてみましょう.
ここではあえて,2次関数のことを何も知らないという前提で描いてみます.
まずは基本となるy=x^2を描きます.
初めに,xが-3から3の整数のときに,yがどのような値になるかを調べてみます.
| x | \cdots | -3 | -2 | -1 | 0 | 1 | 2 | 3 | \cdots |
| y | \cdots | 9 | 4 | 1 | 0 | 1 | 4 | 9 | \cdots |
0周辺をもう少し詳しくみてみましょう.
| x | \cdots | - \frac{3}{4} | - \frac{1}{2} | - \frac{1}{4} | 0 | \frac{1}{4} | \frac{1}{2} | \frac{3}{4} | \cdots |
| y | \cdots | \frac{9}{16} | \frac{1}{4} | \frac{1}{16} | 0 | \frac{1}{16} | \frac{1}{4} | \frac{9}{16} | \cdots |
詳しく調べると,おおよそ以下の図のような形になることが分かります.
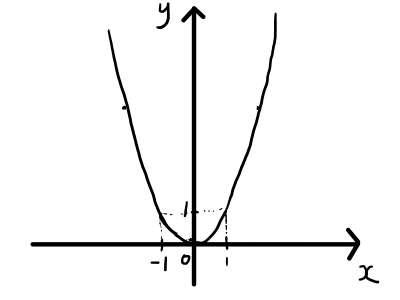
2次関数のグラフは,このような放物線と呼ばれる形になります.
放物線の定義については数学Ⅲでやりますが5気になる人はWikipedia参照.,数学Ⅰの段階では,滑らかなカーブを描いていること,左右対称であることを覚えておきましょう.
続いてy=-x^2を描いてみましょう.
同様にxとyの値の対応を調べると,次のようなグラフになることが分かります.

y=x^2のグラフのように,グラフの形が谷のようになっているグラフを下に凸,y=-x^2のグラフのように,山のような形のグラフを上に凸であるといいます.2次関数のグラフが上に凸になるか下に凸になるかは,aの値(x^2の係数)によって決まります.a>0のとき2次関数のグラフは下に凸に,a<0のとき2次関数のグラフは上に凸になります.
演習.
a>0のとき,aの値を大きくすると,グラフの形はどのように変化するか調べなさい.
2次関数の基本形
y = a(x-p)^2+q (a, p, qは定数,a \neq0)
このような2次関数の形式を基本形といいます.
さっそくaとpとqに適当な値を入れてグラフを描いてみましょう.ここでは,a=1,p=2,q=1として,
y = (x-2)^2+1
さっそくグラフを描いてみましょう.一般形の時と同様に,まずはいくつかの値の対応を調べます.
| x | \cdots | -3 | -2 | -1 | 0 | 1 | 2 | 3 | \cdots |
| y | \cdots | 26 | 17 | 10 | 5 | 2 | 1 | 2 | \cdots |
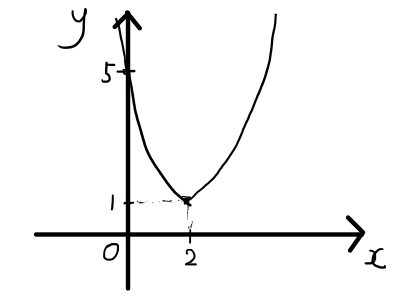
他の値も調べていくと,次のような形になりそうだと分かります.
演習.
基本形のaとpとqに他の値を入れて,その2次関数のグラフを書いてみましょう.
2次関数の山や谷の先端の点を頂点といいます.基本形の特徴は,頂点の座標が(p,q)となっており,頂点の座標がただちに分かることです.また,放物線は左右対称であるといいましたが,対称の軸のことを2次関数のグラフの軸といいます.軸の直線も基本形からただちに求められ,直線x=pが軸となります.
ここで,一般形で書かれた2次関数を基本形に変形することで,一般形の各項の係数と頂点の座標との関係を示したいと思います.一般形から基本形へ変形すると,
\begin{aligned}
y &= ax^2 + bx + c \\
&= a\left(x^2 + \frac{b}{a} + \frac{b^2}{4a^2}\right)-\frac{b^2}{4a} + c \\
&= a\left(x^2 + \frac{b}{2a}\right)^2 - \frac{b^2-4ac}{4a}
\end{aligned}よって頂点の座標は\left(- \frac{b}{2a}, - \frac{b^2-4ac}{4a}\right)であり,軸は直線x = - \frac{b}{2a}であることが分かります.
また,一般形から基本形への変形のことを平方完成といいます.
2次関数の分解形
y = a(x-\alpha)(x-\beta) (a, \alpha, \betaは定数,a \neq0)
上記のような2次関数の形式を,2次関数の分解形といいます.
この形式の意義は,グラフを書けばすぐに分かります.
演習.
分解形のaと\alphaと\betaに値を入れて,その2次関数のグラフを書いてみましょう.
分解形の2次関数をグラフにすると,(a>0,\alpha < \betaとする)
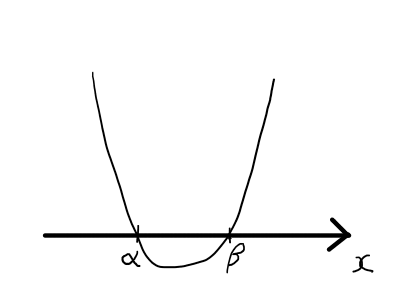
y=0のときのxの値が\alphaと\betaになる,言い換えると,グラフとx軸の交点の座標が(\alpha,0)と(\beta,0)になります.この形式は,2次方程式や2次不等式を解く際に用いられることがあります.
まとめ
最後に2次関数の基本の要点をまとめます.
一般形
f(x) = ax^2+bx+c
基本形
f(x) = a(x-p)^2+q
分解形
f(x) = a(x-\alpha)(x-\beta)
平方完成
一般形を基本形に変形すること.
頂点
2次関数のグラフの谷や山の先端の点.
頂点の座標は基本形の場合(p,q),一般形の場合\left(- \frac{b}{2a}, - \frac{b^2-4ac}{4a}\right)となります.
グラフの軸
2次関数のグラフは左右対称となります.対称の軸のことを2次関数のグラフの軸といいます.
基本形の場合は直線x=p,一般形の場合はx = - \frac{b}{2a}が軸となります.

