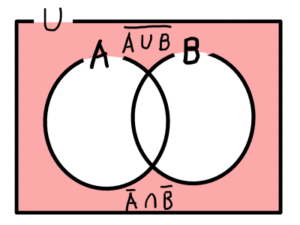
円に内接する四角形の性質
定理.
円に内接する四角形\mathrm{ABCD}について,四角形の対角の和は180^{\circ}である.
証明.
弧\mathrm{CBA}の円周角を\alphaとすると,中心角は2 \alphaとなる.同様に,弧\mathrm{CDA}の円周角を\betaとすると,中心角は2 \betaとなる.
\begin{aligned}
2\alpha + 2 \beta &= 360^{\circ} \\
\alpha + \beta &= 180^{\circ}
\end{aligned}
\alpha = \angle \mathrm{D},\beta = \angle \mathrm{B}なので,
\begin{aligned}
\angle \mathrm{D} + \angle \mathrm{B} &= 180^{\circ}
\end{aligned}
よって,円に内接する四角形の対角の和は180^{\circ}である.
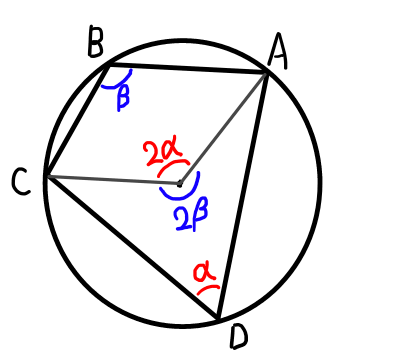
定理.
四角形\mathrm{ABCD}が円に内接するための条件は,1組の対角の和が180^{\circ}となることである.
証明.
\angle \mathrm{B} + \angle \mathrm{D} = 180^{\circ}とする.
\bigtriangleup \mathrm{ABC}の外接円を弧\mathrm{CBA}以外の円周上に点\mathrm{D^{\prime}}をとる.すると,
\angle \mathrm{B} + \angle \mathrm{D^{\prime}} = 180^{\circ}
\angle \mathrm{D^{\prime}} = \angle \mathrm{D}
となるため,円周角の定理の逆より,
点\mathrm{D} は\bigtriangleup \mathrm{ABC}の外接円上に存在する.
よって,1組の対角の和が180^{\circ}であれば,四角形\mathrm{ABCD}が円に内接する.
定理.
円に内接する四角形の1つの内角は,向かい合う角の外角に等しい.
証明.
\angle \mathrm{B} + \angle \mathrm{D} = 180^{\circ}
\mathrm{D}の外角は,180^{\circ} - \angle \mathrm{D} = \angle \mathrm{B}