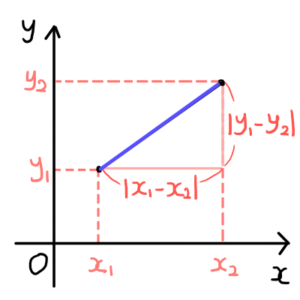
平面上の内分点・外分点・重心の座標
本記事では,主に次の3つの内容について解説します.
- 直線上の線分の内分点と外分点
- 平面上の線分の内分点と外分点
- 平面上の三角形の重心
結果だけでなく,なぜそのような結果になるのか,証明や説明を交えて解説しますので,納得できるまでじっくりと取り組みましょう.
直線上の内分点・外分点
数直線上の線分の内分点について考えます.
なお数直線上の2点\mathrm{A},\mathrm{B}の距離は,点\mathrm{A}の値を a ,点\mathrm{B}の値を b とすると,|a-b|であることを前提とします.
数直線上の線分\mathrm{AB}を m:n に内分する点を\mathrm{P}とします.
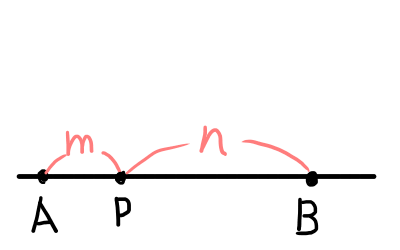
点\mathrm{A}の値を a ,点\mathrm{B}の値を b,点 \mathrm{P} の値を p とします.\mathrm{P}は線分\mathrm{AB}を m:n に内分する点なので,
|a-p| : |p-b| = m:n
が成り立つことから,
m|p-b| = n|a-p|
となります.
ここで,a-p が正のとき,p - b が正となり,
a-p が負のとき,p - b が負となるので,
\begin{aligned}
m(p-b) &= n(a-p) \\
(m + n)p &= na + mb \\
p &= \frac{na + mb}{m + n}
\end{aligned}
よって\mathrm{AB}を m:n に内分する点\mathrm{P}の値は,
\begin{aligned}
p &= \frac{na + mb}{m + n}
\end{aligned}
となります.
外分点の場合も同様に考えることができます.
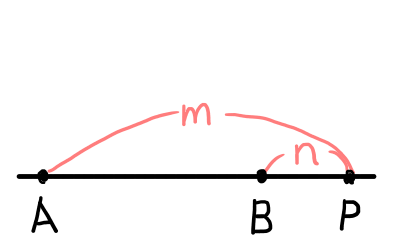
数直線上の線分\mathrm{AB}を m:n に外分する点を\mathrm{P}とし,それぞれの点の値を,点\mathrm{A}は a ,点\mathrm{B}は b,点 \mathrm{P} は p とします.
m:n に外分する点なので,
|a-p| : |p-b| = m:n
が成り立つことから,
m|p-b| = n|a-p|
となります.
ここで,a-p が正のとき,p - b が 負となり,
a-p が負のとき,p - b が正となるので,
\begin{aligned}
m(p-b) &= -n(a-p) \\
(m - n)p &= -na + mb \\
p &= \frac{-na + mb}{m - n}
\end{aligned}
よって\mathrm{AB}を m:n に外分する点\mathrm{P}の値は,
\begin{aligned}
p &= \frac{-na + mb}{m - n}
\end{aligned}
となります.
平面上の線分の内分点
次に平面上の線分の内分点について考えてみましょう.
xy座標上の線分\mathrm{AB}を m:n に内分する点を\mathrm{P}とし,それぞれ,点\mathrm{A}の座標を (x_1, y_1) ,点\mathrm{B}の座標を (x_2, y_2) とします.
このとき以下の命題が成り立ちます.
命題.
線分\mathrm{AB}を m:n に内分する点\mathrm{P}の座標は,
\begin{aligned}
\left( \frac{n x_1 + m x_2}{m + n}, \frac{n y_1 + m y_2}{m + n} \right)
\end{aligned}
x 座標は x_1とx_2の内分点に,y 座標は y_1とy_2の内分点となっています.
線分\mathrm{AB}の内分点の座標は,なぜこのような形になっているのでしょうか?それをこれから考えてみましょう.
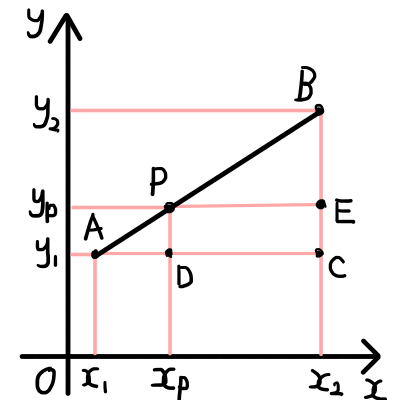
まずは上の図のように,点\mathrm{P}の座標を (x_p, y_p) とします.
さらに \mathrm{C} = (x_2, y_1),\mathrm{D} = (x_p, y_1), \mathrm{E} = (x_2, y_p)とします.
ここまでくれば,各々の方法で納得できるかと思います.
例えば \bigtriangleup \mathrm{ADP}と \bigtriangleup \mathrm{PEB}が相似であり,その相似比が m:n であることは簡単に分かると思います.そこから,x 座標の内分点,y 座標の内分点が点\mathrm{P}の座標となることを導くことができます.
また\bigtriangleup \mathrm{ABC}に関して,\mathrm{BC}と平行な線分 \mathrm{PD}が引かれたと考えることでも同様の結果になります.
平面上の線分の外分点
次に平面上の線分の外分点について考えてみましょう.
xy座標上の線分\mathrm{AB}を m:n に外分する点を\mathrm{P}とし,それぞれ,点\mathrm{A}の座標を (x_1, y_1) ,点\mathrm{B}の座標を (x_2, y_2) とします.
このとき以下の命題が成り立ちます.
命題.
線分\mathrm{AB}を m:n に外分する点\mathrm{P}の座標は,
\begin{aligned}
\left( \frac{-n x_1 + m x_2}{m - n}, \frac{-n y_1 + m y_2}{m - n} \right)
\end{aligned}
この命題の証明は,演習問題としたいと思います.
演習.
線分\mathrm{AB}を m:n に外分する点\mathrm{P}の座標が,
\begin{aligned}
\left( \frac{-n x_1 + m x_2}{m - n}, \frac{-n y_1 + m y_2}{m - n} \right)
\end{aligned}
となることを示せ.
内分点のときと同じ考え方でも構いませんし,他の考え方でも構いません.
平面上の三角形の重心
最後にxy座標上の三角形の重心について解説します.
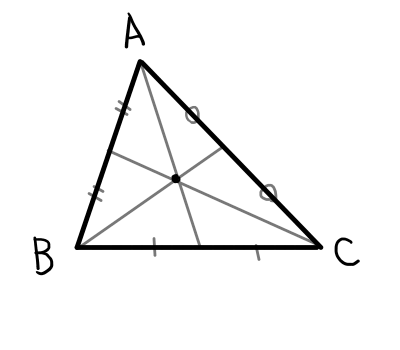
まずは三角形の重心をおさらいします.三角形の重心の特徴は以下の2点です.
- 三角形の3つの中線は1点(重心)で交わる.
- 重心は各中線を2:1に内分する.
より詳しくは以下のページを参照してください.
さて,xy座標上の三角形\bigtriangleup \mathrm{ABC}について,頂点\mathrm{A}の座標を (x_a, y_a) ,頂点\mathrm{B}の座標を (x_b, y_b) ,頂点\mathrm{C}の座標を (x_c, y_c) とします.
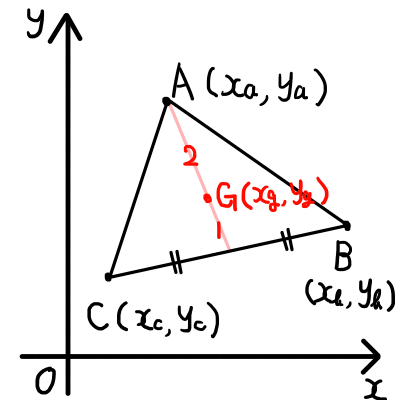
三角形の重心の座標について以下の命題が成り立ちます.
命題.
三角形\bigtriangleup \mathrm{ABC}の重心の座標は,
\begin{aligned}
\left( \frac{x_a + x_b + x_c}{3}, \frac{y_a + y_b + y_c}{3} \right)
\end{aligned}
証明.
三角形\bigtriangleup \mathrm{ABC}の重心\mathrm{G}の座標を (x_g, y_g)とする.
線分\mathrm{BC}の中点を\mathrm{M}とするとその座標は,
\begin{aligned}
\left( \frac{x_b + x_c}{2}, \frac{y_b + y_c}{2} \right)
\end{aligned}
また,重心\mathrm{G}は線分\mathrm{AM}を 2:1 に内分するので,
\begin{aligned}
x_g &= \frac{1 \cdot x_a + 2 \cdot \frac{x_b + x_c}{2}}{3} \\
&= \frac{x_a + x_b + x_c}{3}
\end{aligned}
同様に,
\begin{aligned}
y_g &= \frac{1 \cdot y_a + 2 \cdot \frac{y_b + y_c}{2}}{3} \\
&= \frac{y_a + y_b + y_c}{3}
\end{aligned}
よって,重心\mathrm{G}の座標は,
\begin{aligned}
\left( \frac{x_a + x_b + x_c}{3}, \frac{y_a + y_b + y_c}{3} \right)
\end{aligned}