一般角と動径
数学Ⅱでは三角関数を学習する準備として,一般角と弧度法の2つの概念を導入します.
数学Ⅰの三角比では0^{\circ} \leqq \theta \leqq 180^{\circ}の範囲の角度しか扱いませんでした.三角関数では,あらゆる角度を表現できるように拡張された角である一般角を用います.
この記事では一般角について解説します.
一般角と動径
点\mathrm{O} を端点に持つ半直線を用意し,この線分を点\mathrm{O} を中心に回転させた半直線\mathrm{OP}を考えます.このとき,回転させる前の半直線を始線をいい,回転させた半直線を動径と呼びます.
反時計回り(左回り)に回転した角度を正の数で表し,時計回り(右回り)に回転させた角度を負の数で表すと,全ての実数値の角度を考えることができます.このように角度を回転の向きと大きさで表し,全ての実数値に一般化したものを一般角といいます.
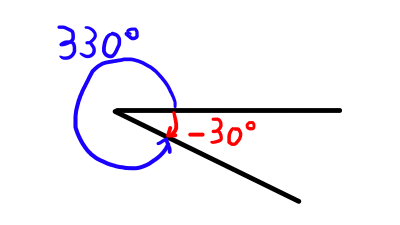
角\theta 回転させた動径を\theta の動径といい,例えば時計回りに30^{\circ}回転させた動径は,-30^{\circ}の動径といいます.
ちなみに,反時計回りに測った角度を正の角,時計回りに測った角度を負の角ということがあります.

また点\mathrm{O} を中心に回転させるため,360^{\circ}回転させると元の半直線と一致します.例えば,-90^{\circ}の動径と,270^{\circ}の動径と,630^{\circ}の動径は一致します.
このことを一般化すると,\theta + 360^{\circ} \times n (n は整数)は一致するということができます.
動径と一般角の演習
演習.
以下の角の動径と角\theta の動径が一致するとき,\theta の値を求めよ.ただし\theta の範囲は,(1)(2)では-180^{\circ} < \theta \leqq 180^{\circ},(3)(4)では0^{\circ} \leqq \theta <360^{\circ}とする.
(1)270^{\circ}
(2)760^{\circ}
(3)1000^{\circ}
(4)-30^{\circ}
演習の解説
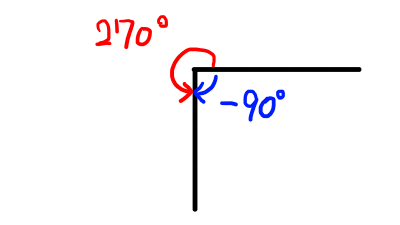
(1)
270^{\circ}は180^{\circ}を超えているので,360^{\circ}を引いて,\theta = -90^{\circ}が答えとなる.
(2)
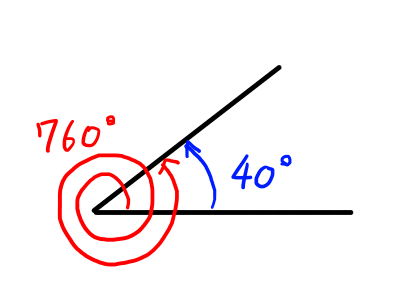
760^{\circ} = 40^{\circ} + 360^{\circ} \times 2 より,\theta = 40^{\circ}となります.
(3)
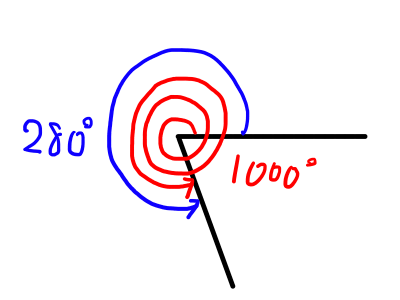
1000^{\circ} = 280^{\circ} + 360^{\circ} \times 2 より,\theta = 280^{\circ}が答えとなります.
(4)
-30^{\circ} = 330^{\circ} + 360^{\circ} \times (-1) より,\theta = 330^{\circ}が答えとなります.
剰余類としての一般角
\theta + 360^{\circ} \times n (n は整数)は一致することから,一般角について,360を法とする剰余類として考えることができます.