三角関数のグラフをかこう!
本記事では三角関数のグラフについて簡単に解説したいと思います.
どうして手書きにこだわったのか,Pythonとmatplotlibを使わなかったのか.コレガワカラナイ
基本的な形
早速ですが,y = \sin{\theta},y = \cos{\theta},y = \tan{\theta}のグラフをかいてみましょう!
y = \sin{\theta}のグラフは以下のようになります.
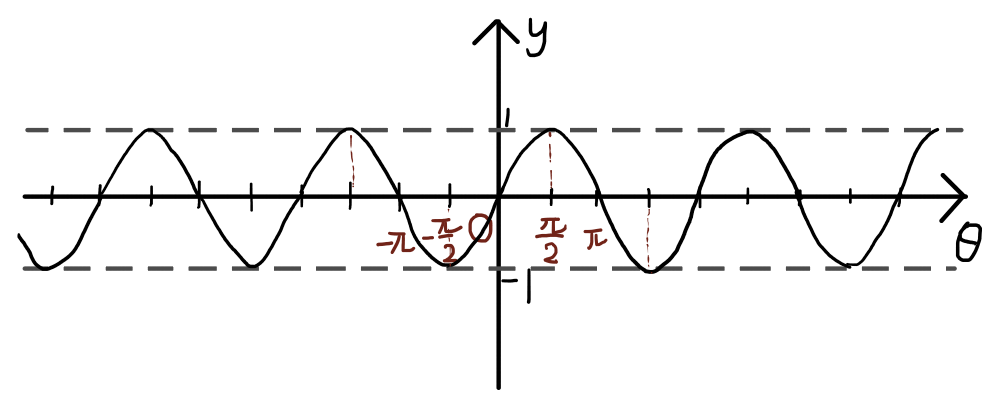
\theta軸のメモリの幅は\frac{\pi}{2}
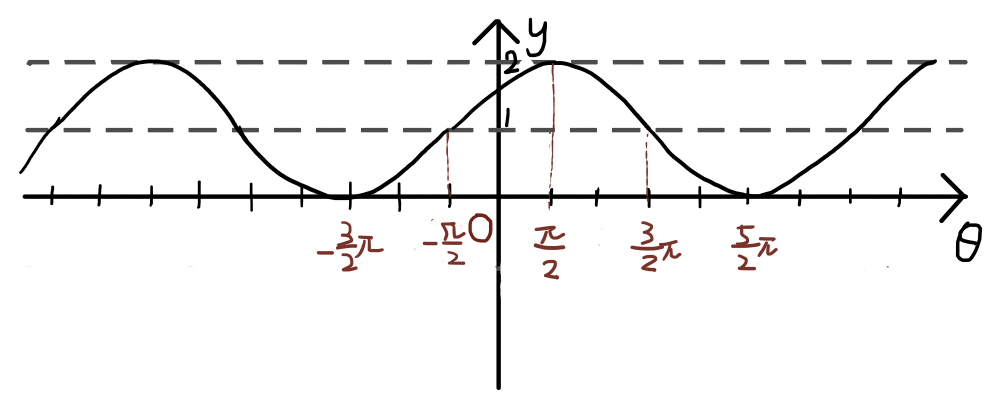
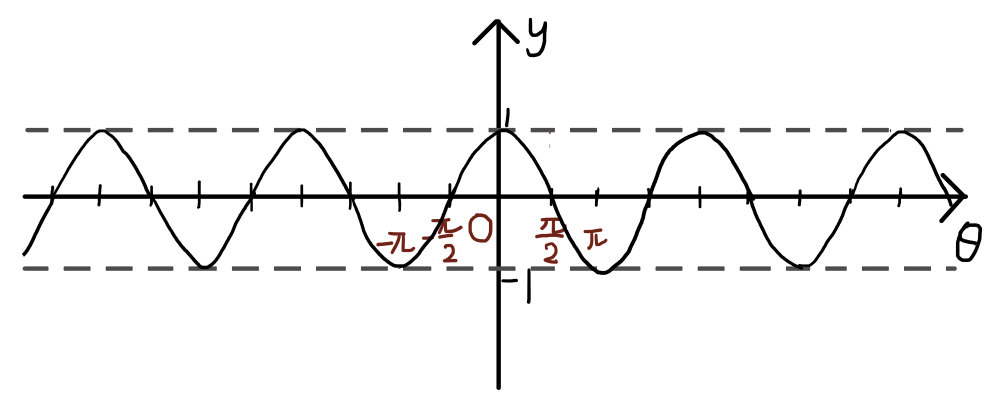
y = \cos{\theta}のグラフは以下のようになります.注意して見ると,y = \sin{\theta}を\theta軸方向に- \frac{\pi}{2}平行移動したものであることが分かります.
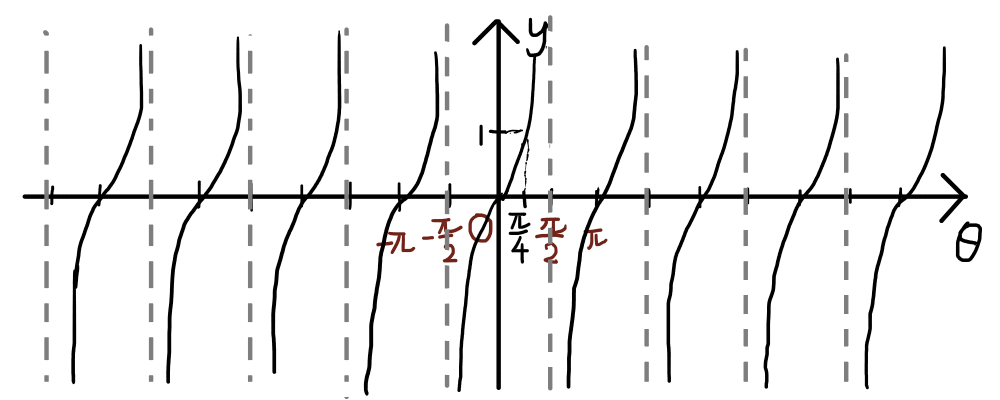
y = \tan{\theta}のグラフは以下のようになります.
灰色の縦点線は漸近線1いくらでも近づくが決して触れることのない線です.
周期について
三角関数のグラフを見ると,全く同じ形を何度も繰り返していることが分かります.このような特性を持つ関数のことを周期関数といいます.
y = \sin{\theta}のグラフの場合,下図の青い線の形が繰り返されてことが分かります.
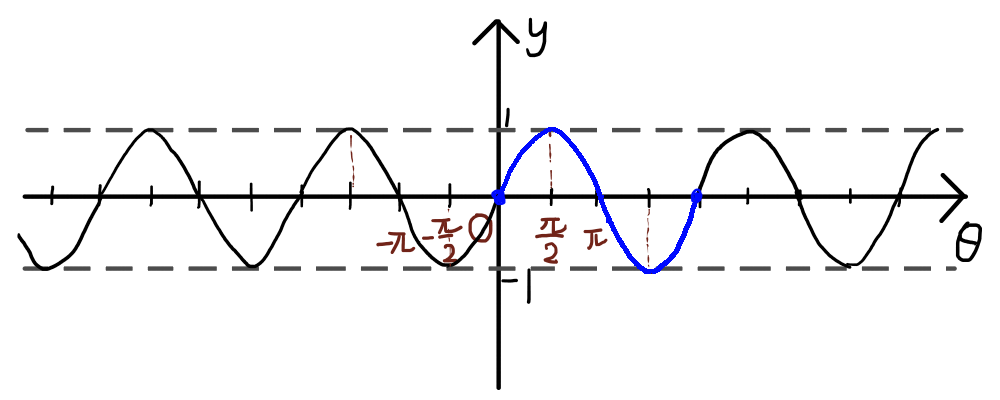
y = \cos{\theta}のグラフの場合,下図の青い線の形が繰り返されています.
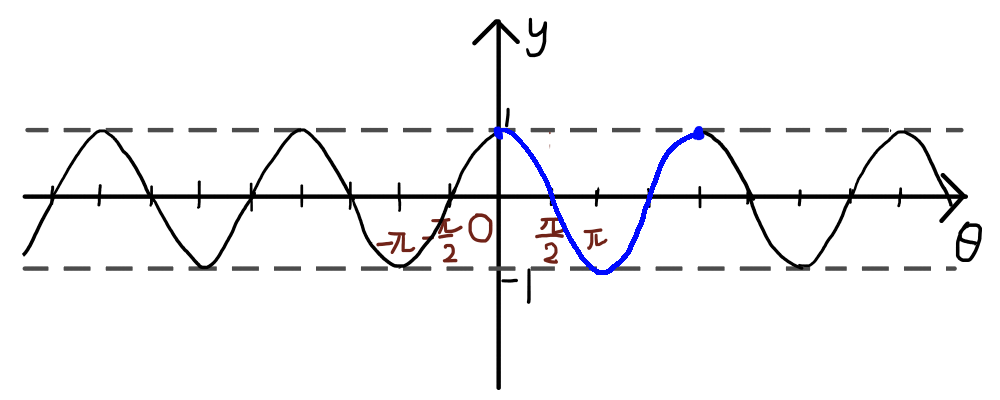
y = \tan{\theta}のグラフの場合は分かりやすいですね.
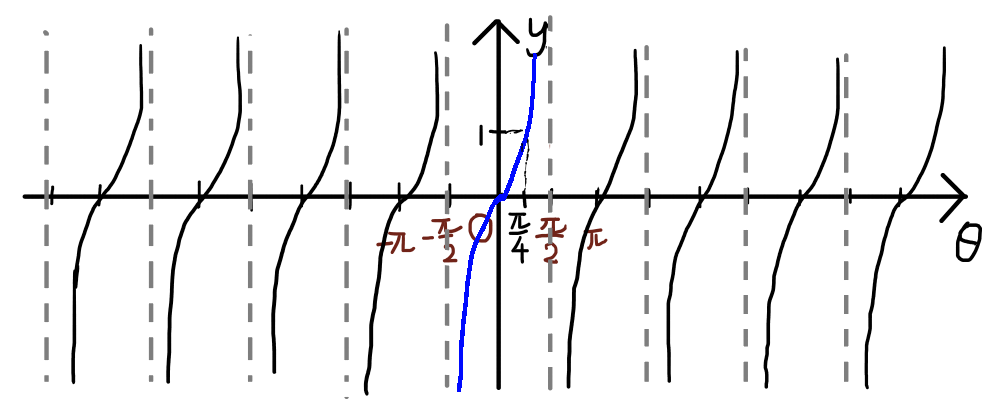
同じ形の繰り返しのうち,最も小さいものを周期(基本周期)といいます.
大雑把にいうと上記のようになりますが,数学的にしっかりと定義すると以下のようになります.
定義.
関数f(x)に関して,任意のxに対してf(x) = f(x + p)が成り立つようなpが存在するとき,この関数のことを周期関数という.
また,そのようなpのうち,正の数で最小のものを,関数f(x)の周期(基本周期)という.
y= \sin{\theta}とy = \cos{\theta}は周期2 \pi,y = \tan{\theta}の周期は\piの関数となります.
周期の変化,グラフの平行移動
数学Ⅰまでに学習した1次関数や2次関数は,値を足したり掛けたりすることで,グラフの形や位置が変わりました.三角関数の場合も同様で,グラフの平行移動や,グラフの高さや周期を変化させることができます.
先に結論をまとめますと以下のようになります.
y = \sin{\theta},y = \cos{\theta},y = \tan{\theta}などの三角関数をy = f({\theta})と表すと,
y = a f \left \{ k \left( \theta - p \right) \right \} + qのグラフは,
y = f({\theta})のグラフを
周期を\frac{1}{|k|}倍して,
y軸方向に|a|倍に拡大して,
\theta軸方向にp,y軸方向にq平行移動させたグラフとなる.
それでは,それぞれの変化を個別に見ていきましょう.
角度を表す変数に数を掛けると,周期が変化します.
y = \frac{1}{4} \cos{\theta}は以下のようなグラフになります.灰色の線が y = \cos{\theta}のグラフです.y = \frac{1}{4} \cos{\theta}のグラフは,周期が8 \piになっています.
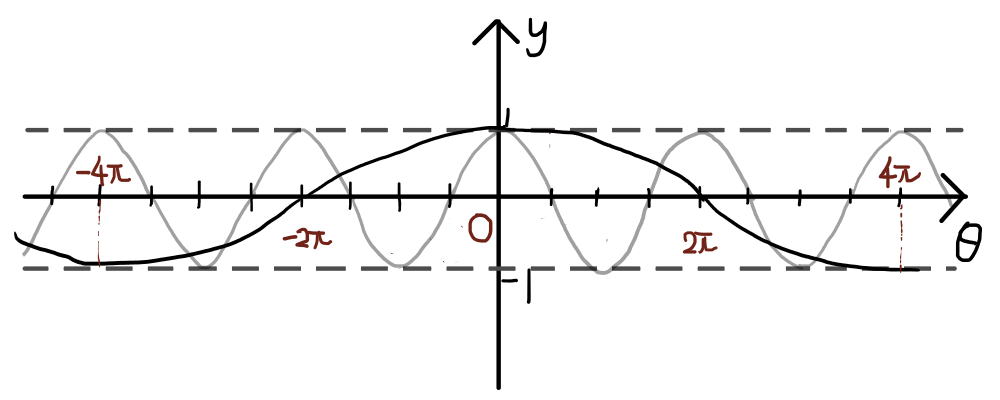
灰色の線はy = \cos{\theta}のグラフ.
周期に関しては次のことが成り立ちます.
\begin{aligned} y = k \sin{\theta} の周期は \frac{2 \pi}{|k|} \\ y = k \cos{\theta} の周期は \frac{2 \pi}{|k|} \\ y = k \tan{\theta} の周期は \frac{\pi}{|k|} \\ \end{aligned}
y軸方向に拡大させることを考えます.
以下のグラフ(黒線)は y = 2 \sin{\theta}のグラフです. y = \sin{\theta}のグラフが,y軸方向に2倍に拡大されています.y軸方向に拡大されているだけなので,周期は2 \piのまま変わりません.

次に\theta軸方向への平行移動を見てみましょう.
y = \cos{\left(\theta - p \right) }の形にすることで,グラフが\theta軸方向へpだけ平行移動します.
以下のグラフ(黒線)は,y = \sin{\left(\theta + \frac{\pi}{2} \right) }です(灰色の線がy = \sin{\theta}).
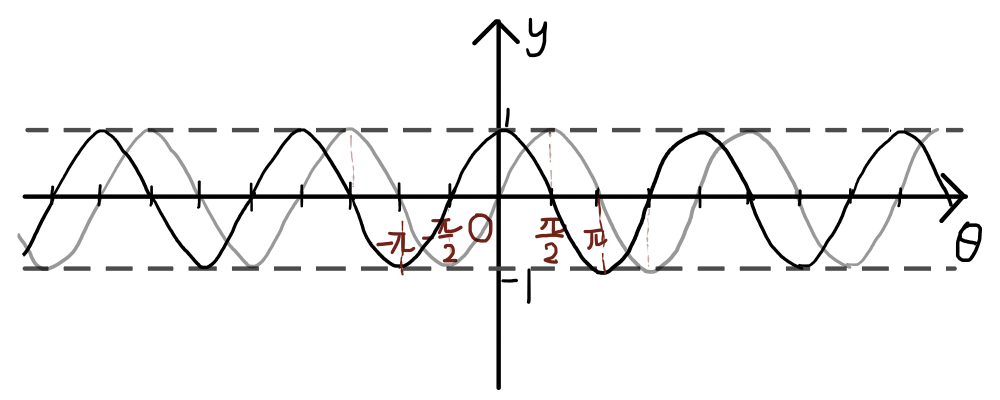
次はy軸方向に平行移動させてみましょう.y = \sin{\theta} + qとすれば,y軸方向にqだけ平行移動させられます.
下のグラフは y = \sin{\theta} + 1のグラフです.
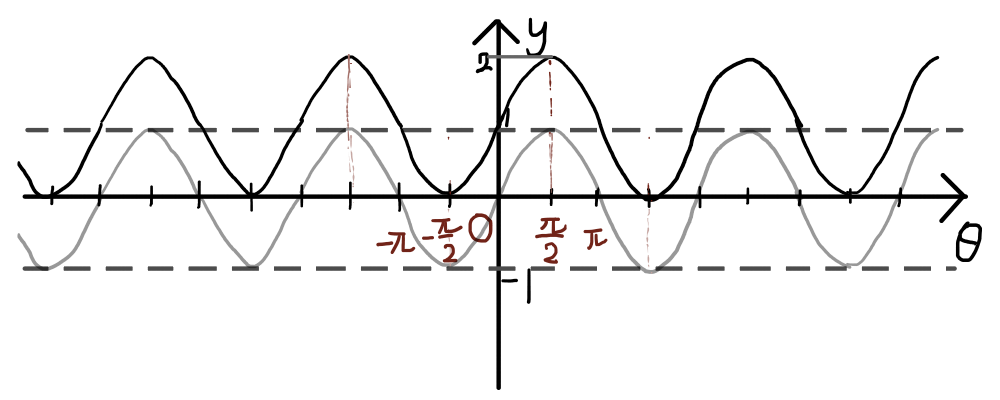
最後に要点を再度まとめます.
y = \sin{\theta},y = \cos{\theta},y = \tan{\theta}などの三角関数をy = f({\theta})と表すと,
y = a f \left \{ k \left( \theta - p \right) \right \} + qのグラフは,
y = f({\theta})のグラフを
周期を\frac{1}{|k|}倍して,
y軸方向に|a|倍に拡大して,
\theta軸方向にp,y軸方向にq平行移動させたグラフとなる.
演習問題
演習問題.
以下の関数のグラフをかきましょう.
\begin{aligned}
y = \cos{\left( \frac{1}{2} \theta - \frac{\pi}{4} \right) } + 1
\end{aligned}
解答例
\begin{aligned}
y &= \cos{\left( \frac{1}{2} \theta - \frac{\pi}{4} \right) } + 1 \\
&= \cos \frac{1}{2} {\left( \theta - \frac{\pi}{2} \right) } + 1
\end{aligned}
よってy = \cos{\theta}のグラフを,周期を4 \piにして,\theta軸方向に\frac{\pi}{2},y軸方向に1平行移動させたグラフをかけばよい.