因数分解の基本 〜共通因数,因数分解の公式など〜
本記事では因数分解について解説したいと思います.
因数分解とは何か?
因数分解とは,整式を整式同士の積の形に分解することです.イメージとしては,展開の逆のような感じです.「因数分解しなさい」と言われた場合は,可能な限り分解する必要があります.
ただし特に条件がない場合は,係数が有理数の範囲で分解します.例えば x^2 - 2 = (x + \sqrt{2} ) (x - \sqrt{2}) といった分解は \sqrt{2} が無理数であるため, x^2 - 2 をこのように分解する必要はありません.
余談になりますが,因数分解という語の「因数」の意味が気になる人もいるでしょう.詳しい説明は省きますが,「因数」とは約数みたいなものだと思ってください.
つまり,因数分解とは,整式を,その整式を割り切る事ができる約数みたいなものの積に分解する操作だと思ってください.素因数分解の整式版と言っても良いかもしれません.
共通因数をくくり出そう
因数分解で最初にやることは,共通因数を見つけることです.以下の式を見てみましょう.
2a^2 + 4ab + 6a
全ての項に 2a があります.この 2a をくくり出してみましょう.
2a^2 + 4ab + 6a = 2a (a + 2b + 3)
2a も a + 2b + 3 もこれ以上分解できないので,上の式はこれで因数分解ができました.
共通因数をくくり出した後でも,さらに分解できることがありますので,分解可能な部分がないか常に気を付けておきましょう.
因数分解の公式(2次)
さて,共通因数を確認したら,次は因数分解の公式を利用できないかを確かめてみましょう.
まずは,2次の因数分解の公式を紹介します.
因数分解の公式(2次).
(1) a^2 + 2ab + b^2 = (a + b)^2
(2) a^2 - 2ab + b^2 = (a - b)^2
(3) a^2 - b^2 = (a + b) (a - b)
(4) x^2 + (a + b)x + ab = (x + a)(x + b)
(5) acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)
因数分解の公式はいくつもありますが,そのほとんどは展開公式の左辺と右辺を入れ替えた式になります.
(1)〜(3)の使用例を見てみましょう.
まずは(1)の公式を使った因数分解の例を見てみます.
4x^2 + 12xy + 9y^2 = (2x + 3y)^2
次に(2)の公式を使った因数分解の例を見てみます.
9x^2 - 30xy + 25y^2 = (3x - 5y)^2
最後に(3)の公式を使った因数分解の例を見てみます.
4 x^2 - 9 y^2 = (2x + 3y) (2x - 3y)
たすき掛け
上記の因数分解の公式のうち,(4)(5)の公式を満たす a ,b ,c ,d を見つけるテクニックに,たすき掛けと呼ばれる手法があります.
acx^2 + (ad + bc)x + bd = (ax + b)(cx + d) のたすき掛けは以下のようになります.

縦に掛けて ac となる a ,c を書きます(下の図の赤い部分).同様に b ,d を書きます.
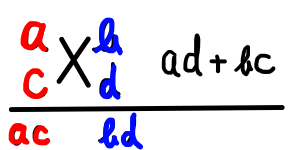
もちろん,上記の分解の方法が1通りでない場合もあるでしょう.
斜めにあるもの同士を掛けて,それぞれを足してみましょう.それが ad + bc ( x の係数)となるような a ,b ,c ,d を見つけましょう!
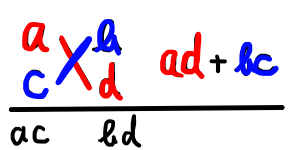
例題として以下の式を因数分解してみます.
2x^2 - x - 6
x^2 の係数は 1 と 2 に分解できます.
- 6 は,1 と - 6,- 1 と 6,2 と -3,-2 と 3 に分解できます.
この中で, ad + bc にあたる部分が - 1 になるのは,以下の組み合わせのときです.
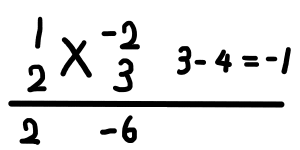
したがって
2x^2 - x - 6 = (x - 2) (2x + 3)
となります.
因数分解の公式(3次)
次に3次の因数分解の式を紹介します.
因数分解の公式(3次).
(6) a^3 + 3a^2 b + 3ab^2 + b^3 = (a + b)^3
(7) a^3 - 3a^2 b + 3ab^2 - b^3 = (a - b)^3
(8) a^3 + b^3 = (a + b)(a^2 - ab + b^2)
(9) a^3 - b^3 = (a - b)(a^2 + ab + b^2)
(10) a^3 + b^3 + c^3 -3abc = (a + b + c)(a^2 + b^2 + c^2 -ab -bc -ca)
(6)〜(10)の例を見てみましょう.
まずは(6)の公式を使った因数分解の例を見てみます.
x^3 + 6x^2 y + 12xy^2 + 8y^3 = (x + 2y)^3
次に(7)の公式を使った因数分解の例を見てみます.
27 x^3 - 54 x^2 + 36 x - 8 = (3x - 2)^3
(8)の公式を使った因数分解の例を見てみましょう.
27x^3 + 125 y^3 = (3x + 5y) (9x^2 -15xy +25y^2 )
(9)の公式を使った因数分解の例を見てみます.
8x^3 - 343 = (2x - 7) (4x^2 +14x +49)
最後に(10)の公式を使った因数分解の例を見てみます.
x^3 + y^3 + xy -1 \\
= x^3 + y^3 + (- 1)^3 -xy(-1) \\
= (x + y - 1)(x^2 + y^2 + 1 -xy + x + y) \\
=(x + y - 1)(x^2 + y^2 -xy + x + y + 1)
せっかくなので,(10)の因数分解の公式の左辺を変形して,右辺になることを確認してみます.
ここでは a^3 + b^3 = (a + b)^3 -3ab(a + b) となることを利用します.
(左辺) \\ = a^3 + b^3 + c^3 -3abc \\ = (a + b)^3 - 3ab(a + b) + c^3 -3abc \\ = (a + b)^3 + c^3 - 3ab(a + b) -3abc \\ = \{ (a + b) + c \} ^3 -3(a + b)c \{ (a + b) + c \} - 3ab(a + b) -3abc \\ = (a + b + c)^3 -3(a + b)c(a + b + c) - 3ab(a + b + c) \\ = (a + b + c) \{ (a + b + c)^2 -3(a + b)c -3ab \} \\ = (a + b + c) ( a^2 + b^2 + c^2 +2ab +2bc + 2ca -3ca -3bc -3ab) \\ = (a + b + c) ( a^2 + b^2 + c^2 -ca -bc -ab) \\
3文字以上あるときのコツ
さて,文字が3つ以上ある場合は,どのように着手すればよいか分からない場合もあるでしょう.
文字が3つ以上ある場合は,1番次数の低い文字に注目して,式を整理しましょう.
a^2 + 2ab + ac + b^2 + bc の因数分解をしてみます.
まず,1番次数の低い文字である c について式を整理します.
a^2 + 2ab + ac + b^2 + bc \\
= (a + b)c + a^2 + 2ab + b^2
a + b が出てきました.ここで,c の無い項に着目すると,(1)の公式が使えることが分かります.
a^2 + 2ab + ac + b^2 + bc \\
= (a + b)c + a^2 + 2ab + b^2 \\
= (a + b)c + (a + b)^2
共通因数 (a + b) が見つかったので,(a + b) でくくって,
a^2 + 2ab + ac + b^2 + bc \\
= (a + b)c + a^2 + 2ab + b^2 \\
= (a + b)c + (a + b)^2 \\
=(a + b) (a + b + c)
このように因数分解することができます.
まとめ
因数分解の方法についてまとめます.
- 共通因数でくくる
- 因数分解の公式が使えないか試す
- 文字が3種類以上ある場合は,1番次数の低い文字で式を整理する
因数分解できているように見えても,さらに分解可能な場合もあるため,これ以上の分解が不可能かどうかを,最後に確認することも重要です.