ニュートン法による√2の近似過程の可視化
\sqrt{2}をニュートン法で求める過程を可視化したいと思います.
ニュートン法の近似過程の可視化
ニュートン法は,関数の値が0になる点を求める手法です.
ここでは,f(x) = x^2 - 2 が0となるxの近似値を求めることで,\sqrt{2}の近似値を求めます.
以下は初期値4の場合の近似過程を可視化したものです.
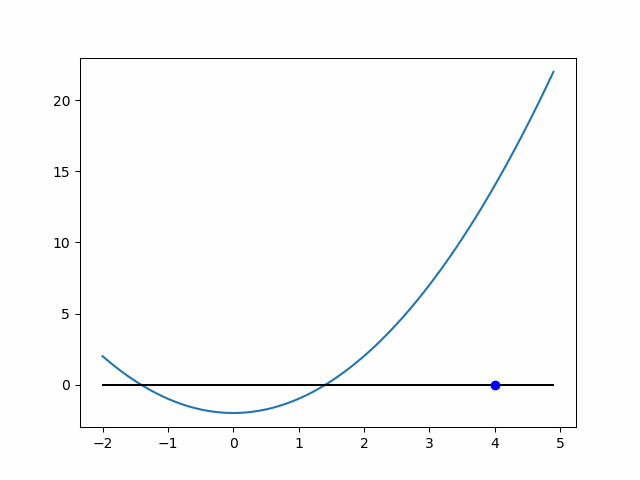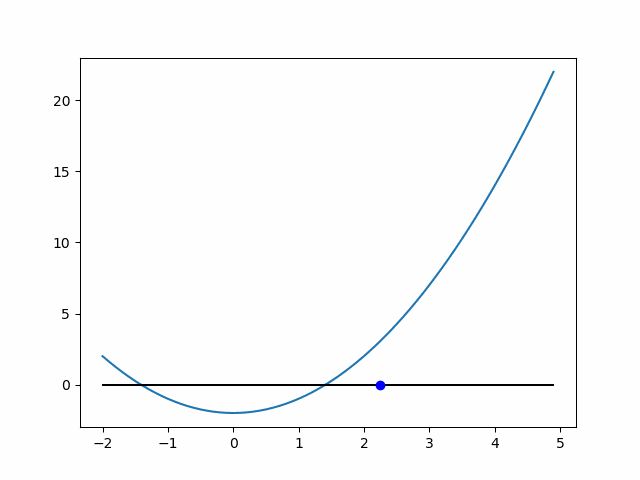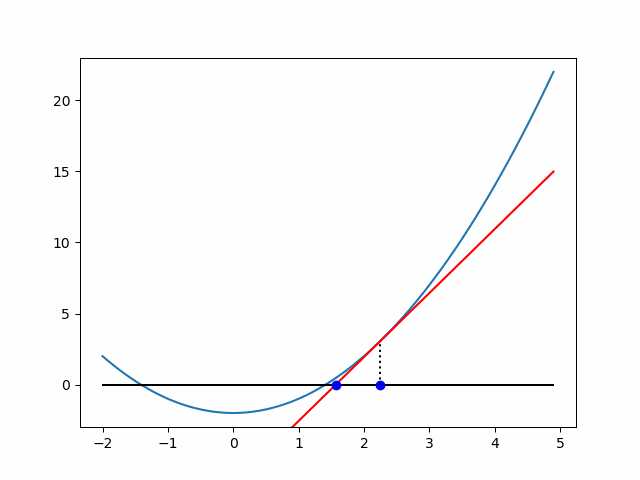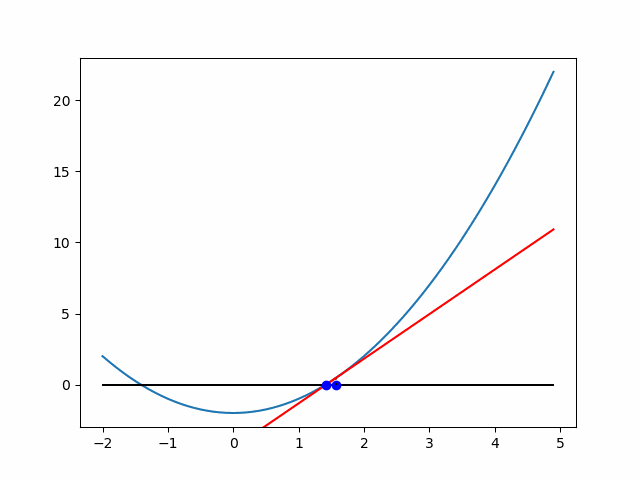
可視化のコード
# xの初期値
curr_x = 4.0
# 変化量がthreshold以下になったら停止
threshold = 5.0e-1
# 変化量
change = 100
# 試行回数
count = 0
print('x{0}:{1}'.format(count, curr_x))
# gifアニメのための画像オブジェクト置き場
artists = []
fig = plt.figure()
# 2次関数とy=0の描画
# xの値の配列
x = np.arange(-0.5, 4.5, 0.05)
# 2次関数
y = x ** 2 - 2
# y=0用の配列
z = x * 0
# 関数の描画
plt.plot(x,y)
# y=0の直線を描画
plt.plot(x,z,'k')
# 軸の調整
plt.ylim(min(y)-1, max(y)+1)
while (threshold < change):
count += 1
# 傾き
grad = 2 * curr_x
# f(curr_x)
f_a = curr_x ** 2 - 2
# 現在のxをプロット
im = plt.plot(curr_x,0, 'bo')
# 現在の描画内容をアニメーションのフレームに追加(点のみ)
artists.append(im)
# 点線の描画
start_y = min(f_a, 0)
end_y = max(f_a, 0)
line_x = np.full(20, curr_x)
line_y = np.linspace(start_y, end_y, 20)
im2 = plt.plot(line_x, line_y, 'k', linestyle = ":")
# 点線と初期点の描画
im2.extend(im)
# 描画内容をアニメーションのフレームに追加
artists.append(im2)
#接線の描画
tan_y = f_a + grad * (x - curr_x) #接線描画用y座標
im3 = plt.plot(x, tan_y, 'r-')
# 接線と点線と初期値の描画
im3.extend(im2)
# 現在の描画内容をアニメーションのフレームに追加
artists.append(im3)
# 更新後の点を求める
change = abs(f_a / grad)
curr_x = curr_x - f_a / grad
print('x{0}:{1}'.format(count, curr_x))
# 更新後の点を描画
im4 = plt.plot(curr_x, 0, 'bo')
# 更新後の点と接線と点線と初期値の描画
im4.extend(im3)
# 現在の描画内容をアニメーションのフレームに追加
artists.append(im4)
anime = animation.ArtistAnimation(fig,artists,1000,2000)
plt.show()
anime.save('sqrt2.gif', writer="pillow")
