問題を解くときの着眼点の重要性

　問題を解くときは着眼点や発想が大切です．しかし，同時に複数の着眼点があった場合に，どの着眼点に着目するかも重要になります．例えば，パッと閃いた発想が回り道ということもあります．

　本記事では，以下の図形問題を通して，着手する発想により，いかに解答の難易度や計算時間に影響が現れるか見てみましょう．

問題

　以下の図は半径 4cm の円であり，点\mathrm{A} ，\mathrm{B} ，\mathrm{C} ，\mathrm{D} は円周を4等分している．
　このとき，以下の図の赤く塗られた部分の面積を求めよ．

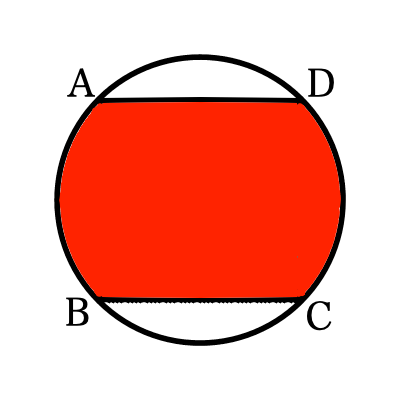
解答例1

　１つ目の方針です．
　まず，下の図の青い部分の面積を求めます．その後，円の面積から青い部分の面積の2倍を引くことで，解答となる面積を求めます．

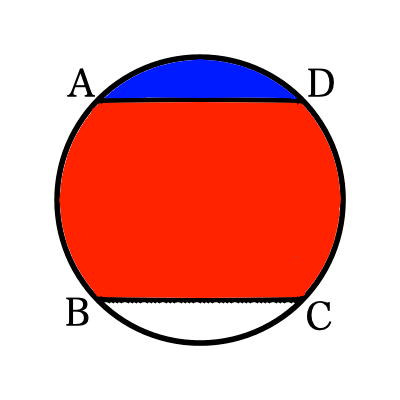
解答例1．
円の中心を\mathrm{O} とする．
弧と中心角の関係より，
\angle \mathrm{AOB} = \angle \mathrm{BOC} = \angle \mathrm{COD} = \angle \mathrm{DOA} = 90^{\circ} である．
また，弧と中心角と円周角の関係より，
\angle \mathrm{ABD} = \angle \mathrm{ADB} = \angle \mathrm{DBC} = \angle \mathrm{BDC} = 45^{\circ} である．
よって，\triangle{\mathrm{ABD}} と \triangle{\mathrm{CBD}} は底辺 8cm，高さ 4cm の直角二等辺三角形である．

図の青い部分の面積は，
(円の面積) - (四角形 \mathrm{ABCD} の面積) \div 4 で求められる．
つまり，
( 4 \times 4 \times \pi - 8 \times 4 \times \frac{1}{2} \times 2) \div 4 = (16 \pi - 32) \div 4 = 4 \pi - 8
(4 \pi - 8) cm^2

よって求める面積は，
4 \times 4 \times \pi - 2(4 \pi - 8) = 8 \pi + 16
(8 \pi + 16) \mathrm{cm}^2 となる．

　答えを求めることはできましたが，少し煩雑で遠回りした気分になります．

解答例2

　２つ目の方針は次の通りです．
　図の赤い部分（面積を求める部分）を2つの扇形と2つの直角三角形に分解して，それぞれの面積を考えます．

解答例2．
円の中心を\mathrm{O} とする．
弧と中心角の関係より，
\angle \mathrm{AOB} = \angle \mathrm{BOC} = \angle \mathrm{COD} = \angle \mathrm{DOA} = 90^{\circ} である．
よって求める面積は，底辺 4 \mathrm{cm}，高さ 4 \mathrm{cm} の直角三角形2つ（\triangle{\mathrm{AOD}} と\triangle{\mathrm{BOC}} ）の面積と，半径 4 \mathrm{cm} の円における中心角 90^{\circ} の扇形２つ分の面積を合わせたものである．

よって，求める面積は，
2( 4 \times 4 \times \frac{1}{2}) + 2(4 \times 4 \times \pi \times \frac{1}{4}) = 8 \pi + 16
(8 \pi + 16) \mathrm{cm}^2 となる．

　こちらの方が，計算が少なくて済みました．また，計算が早い人であれば，1分もかからずに解けるでしょう．

まとめ

　２つの方針で問題を解きましたが，いかがだったでしょうか．

　採用する方針や着眼点によって，問題の難易度や，解答のスピードは大きく変わります．これは大学入試においても同様で，数学教員の中には，解き方によって難易度や解答時間が大きく変わる問題を作ることが得意な方もいます．非常に時間のかかる解法，普通の解法，やや早い解法，一瞬で解ける解法が全て想定された入試問題もあります．

　時間のかかる解法や，難易度の高い解法に迷い込まないようにするためには，ある程度，解法のパターンを知っておく必要があります．また，ひとつの考え方に固執しすぎないことも重要です．

　私も上手い解答を作ることは苦手ですが，良い解答が作れるよう一緒に頑張りましょう．