y=xに関する対称移動を考える

2次関数の問題には，グラフの軸に関して対称移動させるものや，原点に関して対称移動させるものがありました．
簡単におさらいしておきますと，関数y=f(x)をx軸に関して対称移動させると，-y=f(x)，y軸に関して対称移動させると，y=f(-x)，原点に関して点対称なグラフにすると-y=f(-x)となります．

では，直線y=xに関して対称移動させると，関数はどのように変化するでしょうか．

y=x^2を対称移動させる（代表点を移動させる）

平面上の線対称移動とは，元の点と線対称となるように点を移動させることです．線対称となる2つの点を結ぶと対称の軸と垂直に交わり，また，それぞれの点と直線との距離が等しくなります．

それではy=x^2を直線y=xに関して対称移動させてみます．

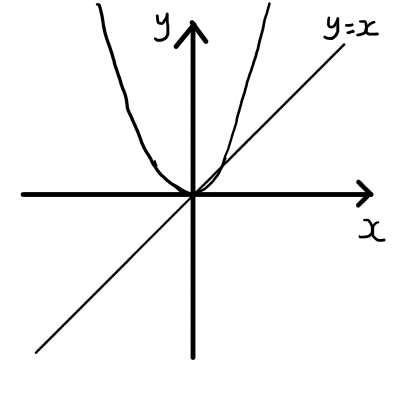
まずは，y=x^2上の代表的な点がどこに移動するかを調べてみましょう．

プロットすると以下の図のようになります．

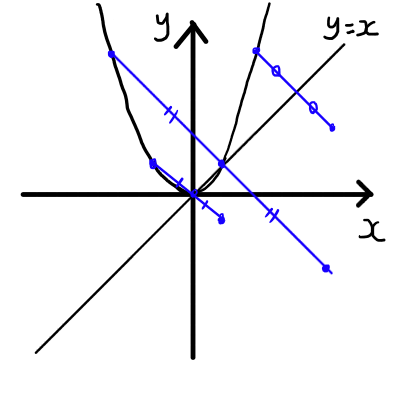
おおよその形が見えてきました．

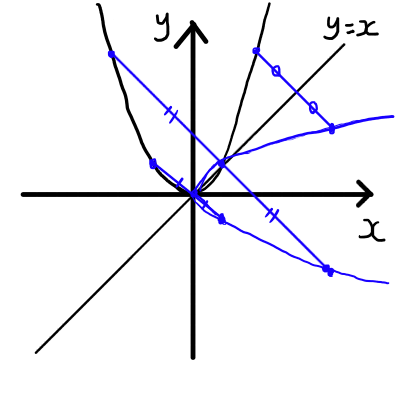
y=x^2を対称移動させる（紙を使って移動させる）

線対称移動は軸で折り返すイメージです．

正方形の紙を使って，y=x^2を直線y=xに関して対称移動させてみます．正方形の紙を用意して実際に動かしてみましょう．薄い紙がオススメです．頭の中でイメージするのもアリです．

まずは，正方形の紙のちょうど真ん中が原点となるように軸を描き，その上に2次関数y=x^2のグラフを描きます．

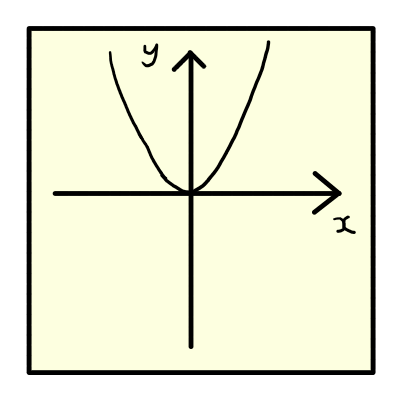
直線y=xに沿って折ります．グラフを描いた面が内側になるように折りましょう．そうすると，直角二等辺三角形ができ，下の図のように，裏側のグラフが透けて見えると思います．

最後に，グラフを描いた面が裏側になるように開きましょう．

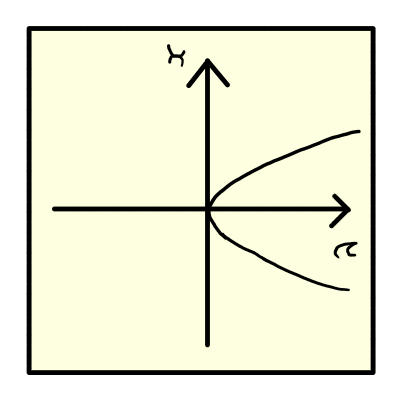
上の図のようなグラフが透けて見えるはずです．

点を対称移動させる（一般化する）

どうやらy=x^2を直線y=xに関して対称移動させると，x=y^2になるようです．

一般化するために，点(a,b)を直線y=xに関して対称移動させるとどうなるか，調べてみたいと思います¹数学Ⅱの知識を使ったり使わなかったりしているので，少し読みにくいかもしれません．．

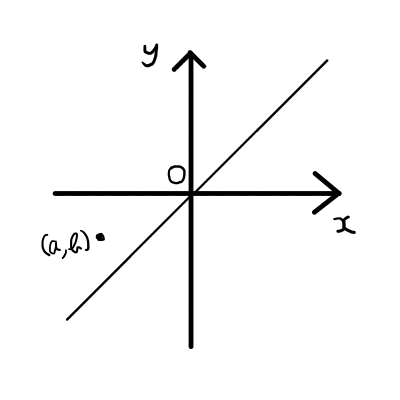
初めに，点(a,b)を通り，直線y=xと垂直に交わる直線を考えてみましょう
直線y=xと垂直に交わることから，求める直線の傾きは直線-1なので，²点(a, b)を通り，傾きがmの直線は方程式
y-b = m(x-a)
で表されます．
（証明）
傾きがmの直線の方程式はy=mx+\alpha
そこにx=a，y=bを代入して，
b = ma + \alpha
\alpha = b - ma
\alphaをもとの式に代入して，
y = mx + b - ma
y-b = m(x-a)

\begin{aligned}
y-b &= -1(x-a) \\
y &= -x +a + b 
\end{aligned}

求めたい直線がy=-x+a+bであることが分かりました．
次に，2つの直線の交点を求めます．y=xとy=-x+a+bの連立方程式を解くと，交点が\left( \frac{a+b}{2}, \frac{a+b}{2} \right)だと分かります．

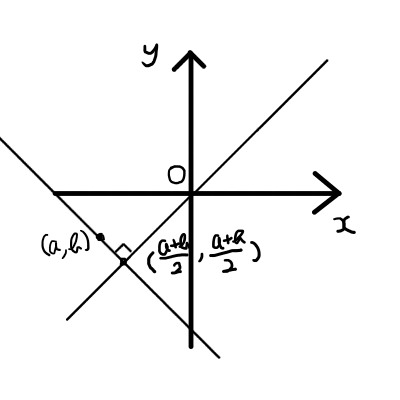
最後に対称移動した後の座標を求めましょう．
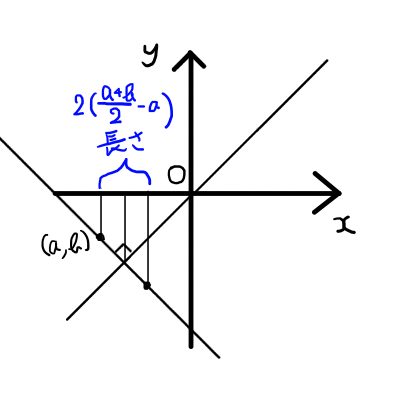
a<bのとき，元の点のx座標と対称移動した点のx座標の差が，2\left( \frac{a+b}{2} - a \right)であることが分かります．ここから，対称移動後の点のx座標は，

\begin{aligned}
a + 2\left( \frac{a+b}{2}-a \right) &= a+a+b-2a \\
&= b 
\end{aligned}

x座標はbであることが分かりました．
同様に考えると，y座標がaであることが求まります．

a>bのとき，移動前と移動後の点のx座標の差が，2\left( a - \frac{a+b}{2} \right)であり，移動後の点のx座標がa - 2\left( a - \frac{a+b}{2} \right)=bであることが分かります．同様に，y座標はaとなります．

a=bの場合は，点(a,b)も点(b,a)も同じです．

これらの結果をまとめると，点(a,b)を直線y=xに関して対称移動すると，点(b,a)となることが分かります．

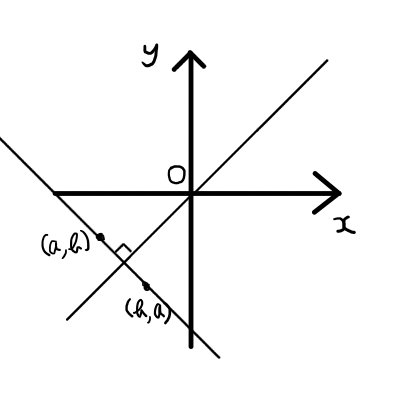
直線y=xに関して対称移動させるとyとxが入れ替わってしまうようです．
確かに，前の節で触れた2次関数y=x^2を対称移動させた式も，x=y^2となっていました．

遊びの提案（演習問題）

直線y=2xに関する対称移動について考えてみましょう．

別の考え方と大学の数学

今回は素朴な手法や，地道な計算によって，対称移動について調べました．これらもとても大事な手法ですが，全く異なる考え方を思いついた人もいるでしょう．その一例を紹介します．

線対称の軸y=xは45°傾いています．そこで，y=xに関する対称移動を，
1．原点を中心に平面ごと左に45°回転させる（座標は回転させずにそのまま固定）．
↓
2．y軸に対して線対称移動をする．
↓
3．平面を右に45°回転させる．
といった操作だと考えることができます．

大学で行列を学ぶと，この考え方を簡単に表現することができます³行列による合同変換です．左の行列から順に操作3，操作2，操作1を表しています．
\begin{pmatrix} \cos -45^{\circ} & - \sin -45^{\circ} \\ \sin -45^{\circ} & \cos -45^{\circ} \\ \end{pmatrix} \begin{pmatrix} -1 & 0 \\ 0 & 1 \\ \end{pmatrix} \begin{pmatrix} \cos 45^{\circ} & - \sin 45^{\circ} \\ \sin 45^{\circ} & \cos 45^{\circ} \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix} ．
これから大学生になる読者の皆さんは，お楽しみに！

「勝手気ままに高校数学」シリーズ一覧へ