「アキレスと亀」から極限を考えよう!
私が高校生だった頃,数学Ⅱの微分積分の単元に入る前に,「ゼノンのパラドックス」の紹介とそれに関する課題が出ました.高校数学では誤魔化される,「極限」「無限」「連続性」について考えるヒントになるからでしょう.
その中でも「アキレスと亀」について考える機会が多く,1日中考え続けて,数学の上級クラスで唯一「教卓でパラドックスの解説を行う」という課題をクリアすることができました1そんなに難しい問題ではないので,自分一人しか課題をクリアした人がいないのは不思議ですね.おそらく受験と関係ないことには興味も持たない,つまらない考え方の人が多かったのでしょう.もしくは答えが決まっている問題でないと自信を持って発表できなかったのかもしれません..受験と関係のないことを1日中考え続ける,これが私の数学をする能力の下地の一部になっていると思います.
本記事では,「アキレスと亀」について紹介し,「極限」について考えるヒントにつなげたいと思います.
アキレスと亀
足の速いアキレスという人間と,アキレスよりも足の遅い亀がいます.
アキレスと亀はレースをするのですが,そのままでは当然アキレスが勝ってしまい,面白くありません.
そこで,アキレスにハンデを与えることにしました.アキレスのスタート位置を亀のスタート位置より後ろにしたのです.
すると不思議なことが起こります.
レースが始まった後,アキレスは亀のスタートラインまで辿り着きます.その時,亀はスタートラインよりも前に進んでいます.その時亀がいた地点にアキレスが辿り着いた頃には,亀はさらに前に進んでいます.さらにその時に亀がいた地点にアキレスがたどり着く頃には,亀はもちろん前に進んでいます.
手順を以下にまとめましょう.
手順.
ある時点で亀がいる場所までアキレスが進む.すると,アキレスが進んでいる間に亀も進んでいる.その時点で亀がいる場所までアキレスが進む.すると,アキレスが進んでいる間に亀も進んでいる.
この手順は何回でも繰り返すことができます.よって,アキレスは亀に追いつくことができません.アキレスは亀よりも足が速いにもかかわらずです.
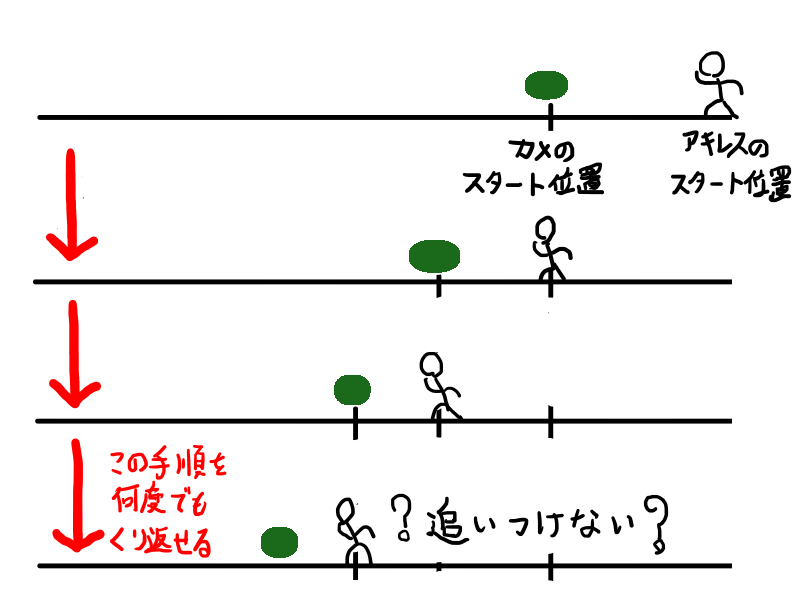
さて問題です.
このパラドックスは何故生じているのでしょうか?「アキレスは亀に追いつけない」は本当でしょうか?
アキレスと亀の種明かし
アキレスは亀に追いつけない?そんなはずはないでしょう.アキレスの方が速い以上,いずれ亀に追いつきます.ではなぜ,亀がアキレスより前にいる状態を無限に繰り返すことができるのでしょうか.
実は上記の手順は,アキレスが亀に追いつく地点までを細かく区切っているだけなのです.区間の長さはだんだん短くなっています.手順1回にかかる時間も短くなっていきます.
ここで次のような例を考えてみましょう.
アキレスは200m/分で,亀は100m/分で移動します2この亀は普通の人間が歩く速さと同じ速さで移動していますね.すごい!.アキレスは亀より100m後方よりスタートします.
この時,アキレスが亀に追いつくのは何分後でしょうか?また,追いつくのはアキレスが何m移動した地点でしょうか?簡単な計算で求められますね.アキレスが亀に追いつくのは1分後で,200m移動した地点で追いつきます.
この設定で上記の手順を行うと以下の図のようになります.
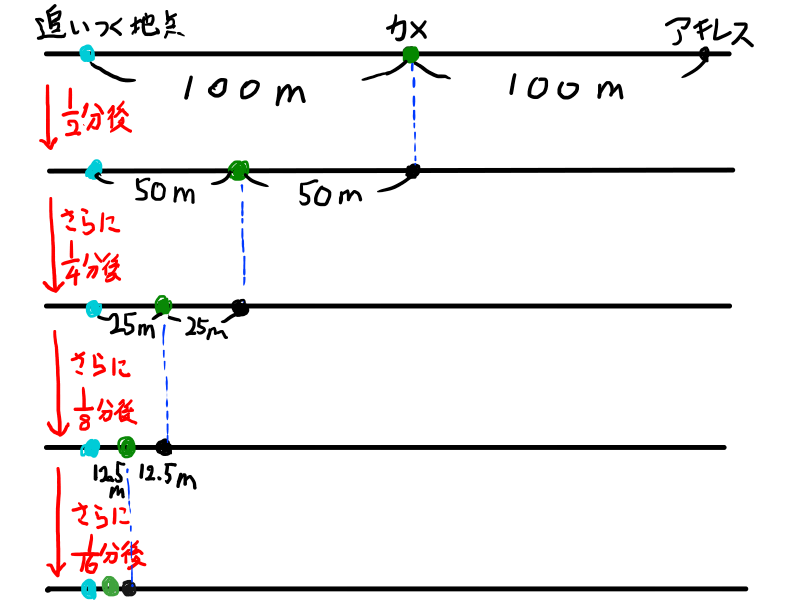
この手順を続けると,さらに\begin{aligned} \frac{1}{32} \end{aligned}分後,さらに\begin{aligned} \frac{1}{64} \end{aligned}分後,\begin{aligned} \frac{1}{128} \end{aligned}分後,というようにだんだん手順の時間が短くなっています.経過した時間を足していくと,
\begin{aligned}t = \sum_{k=1}^{n} \frac{1}{2^k} \end{aligned}
となり,時間が1分を超えることはありません(これを確認するのは少し難しいかもしれません).そして,手順を何度繰り返しても,アキレスの移動距離が200mを超えることはありません.
以上が「アキレスと亀」のざっくりとした説明になります.
極限につながる話
上記の手順を何度も何度も繰り返すと「アキレスが亀に追いつく地点」に限りなく近づくことができます.
これは極限にとても似ています.限りなく近づいていくけれど,重なることはないという点が重要です.
微分を学習するときは冒頭に以下のような式が表れます.
\begin{aligned} \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \end{aligned}
この \begin{aligned} \lim_{h \to 0} \end{aligned} の意味は大雑把にいうと h を0に限りなく近づけるというものです.ここでのポイントは h が0になることは決してないということです.そのため「分母が0じゃん,やってはいけない式じゃん」とはならないのです.
まとめ
高校時代に「アキレスと亀」を教えてくれた先生は,極限も「アキレスと亀」も決して重ならない操作であることを伝えようとしてくれたのだと思います.本記事で,皆さんにもそのことが伝っていれば幸いです.
その先生との数学に関するやり取りは他にもあるのですが,またの機会にお話しすることにしましょう.

