一度は証明したい三角比の重要定理 〜基本的な公式,正弦定理,余弦定理〜
本記事では,三角比の重要な定理,公式を証明したいと思います.証明方法は記事に書かれているものが全てではありませんので,自力で考えてみるのも良いでしょう.証明を経験することで,定理の暗記もスムーズなものとなり,また,忘れてしまった場合も自力で導き出せるようになります.
なお特別に断りがない場合は,執筆時点の学習指導要領に合わせて,0^{\circ} \leqq \theta \leqq 180^{\circ}とします.
基本的な公式
公式.
\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}
証明.
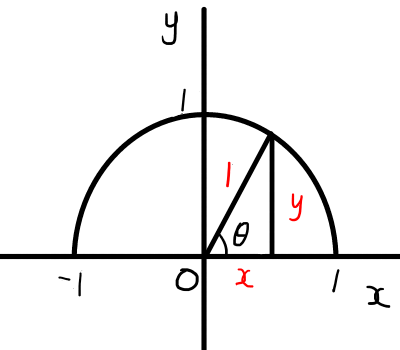
単位円で考えると,\cos{\theta} = x,\sin{\theta} = y,\tan{\theta} = \frac{y}{x}なので,
\tan{\theta} = \frac{y}{x} = \frac{\sin{\theta}}{\cos{\theta}}
公式.
\sin^2{\theta} + \cos^2{\theta} = 1
証明.
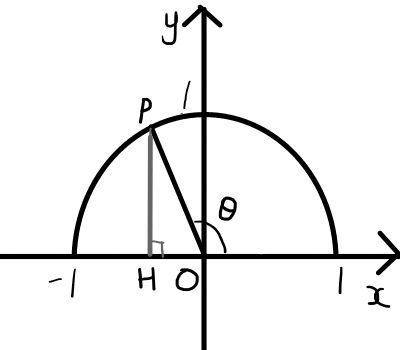
単位円について,円周上の点Pからx軸への垂線の足をHとおき,\bigtriangleup \mathrm{PHO}に関して三平方の定理より,
\sin^2{\theta} + \cos^2{\theta} = 1
公式.
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}
証明.
\sin^2{\theta} + \cos^2{\theta} = 1の両辺に\cos^2{\theta} で割って,1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}
余角公式 ( 90^{\circ} -\theta )
余角公式 (0^{\circ} < \theta < 90^{\circ} )
\sin{(90^{\circ} - \theta)} = \cos{\theta}
\cos{(90^{\circ} - \theta)} = \sin{\theta}
\tan{(90^{\circ} - \theta)} = \frac{1}{\tan{\theta}}
証明.
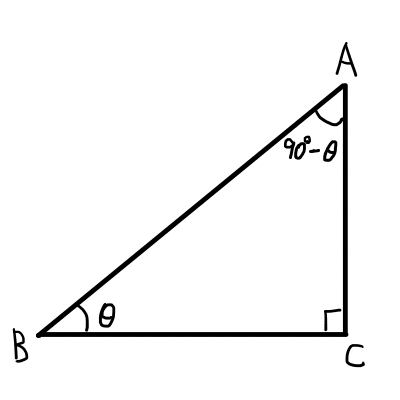
直角三角形の1つの鋭角を\thetaとすると,もう一方の鋭角は90^{\circ} - \thetaとなる.そこから,余角公式をただちに求めることができる.
正弦定理
正弦定理.
\bigtriangleup \mathrm{ABC}の外接円の半径をRとすると,
\frac{a}{\sin{A}} = \frac{b}{\sin{B}} = \frac{c}{\sin{C}} = 2R
証明.
\frac{a}{\sin{A}} = 2Rを証明する.
A < 90^{\circ}の場合,
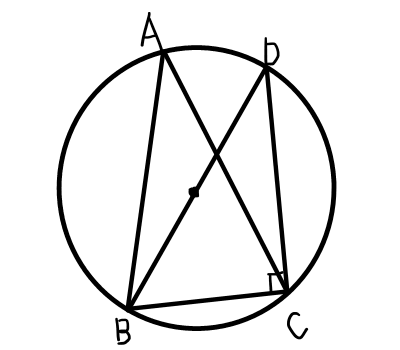
同一の弧に対する円周角は等しいので,円周上の点\mathrm{D}を\mathrm{BD}が外心円の中心を通るようにすると,
\angle \mathrm{BAC} = \angle \mathrm{BDC}
\angle \mathrm{ABD} = 90^{\circ}より,
\begin{aligned}
\sin{D} &= \frac{a}{2R} \\
a &= 2R \sin{D} \\
a &= 2R\sin{A} \\
\frac{a}{\sin{A}} &= 2R
\end{aligned}
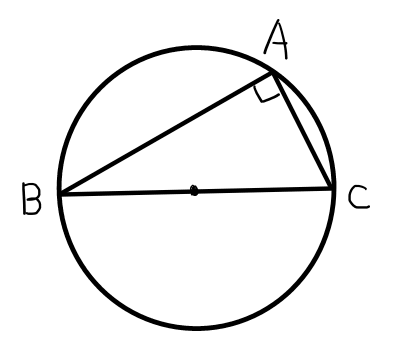
A = 90^{\circ}の場合,
辺\mathrm{BC}は外心円の中心を通るので,
a = 2R = 2R \cdot 1 = 2R \sin{A}
よって,
\frac{a}{\sin{A}} = 2R
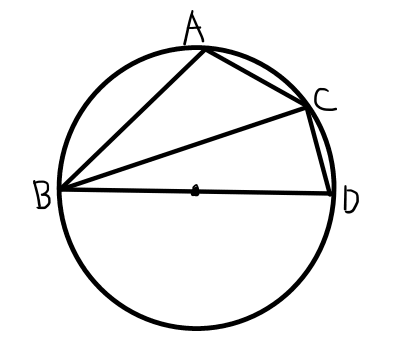
A > 90^{\circ}の場合,
\mathrm{BD}が外接円の中心を通るように,円周上に点\mathrm{D}をとる.四角形\mathrm{ABDC}は円に内接しているため,円に内接する四角形の性質より,
A = 180^{\circ} - Dより,\bigtriangleup \mathrm{BCD}に着目して,
\begin{aligned}
\sin{D} &= \frac{a}{2R} \\
a &= 2R \sin{D} \\
a &= 2R\sin{A} \\
\frac{a}{\sin{A}} &= 2R
\end{aligned}
よって,\frac{a}{\sin{A}} = 2Rが成り立つ.
また,\frac{b}{\sin{B}} = \frac{c}{\sin{C}} = 2Rも同様に求められる.
余弦定理
第1余弦定理.
\bigtriangleup \mathrm{ABC}について以下の等式が成り立つ.
\begin{cases}
a &= b \cos{C} + c \cos{B} \cdots (1) \\
b &= c \cos{A} + a \cos{C} \cdots (2) \\
c &= a \cos{B} + b \cos{A} \cdots (3) \\
\end{cases}
証明.
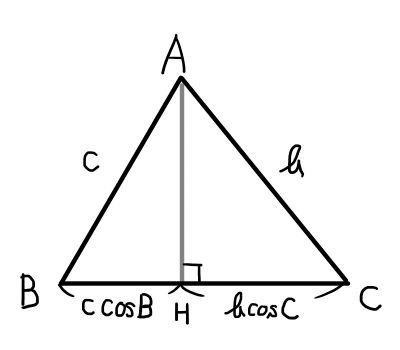
頂点\mathrm{A}から辺\mathrm{BC}への垂線の足を\mathrm{H}とする.
\bigtriangleup \mathrm{ABH}に関して,
\begin{aligned}
\cos{B} &= \frac{\mathrm{BH}}{c} \\
\mathrm{BH} &= c\cos{B}
\end{aligned}
\bigtriangleup \mathrm{ACH}に関して,
\begin{aligned}
\cos{C} &= \frac{\mathrm{CH}}{b} \\
\mathrm{CH} &= b\cos{C}
\end{aligned}
a = \mathrm{BH} + \mathrm{CH} = b \cos{C} + c \cos{B}
他二つも同様に求められる.
第2余弦定理.
\bigtriangleup \mathrm{ABC}について以下の等式が成り立つ.
a^2 = b^2 +c^2 -2bc\cos{A}
b^2 = c^2 +a^2 -2ca\cos{B}
c^2 = a^2 +b^2 -2ab\cos{C}
証明.
第1余弦定理より,
(1) \times a - (2) \times b - (3) \times cをまとめると,
a^2 = b^2 +c^2 -2bc\cos{A}
他も同様に求められる.
第1余弦定理を用いない証明もしてみましょう.ここでは,座標を用いて証明します.
証明.
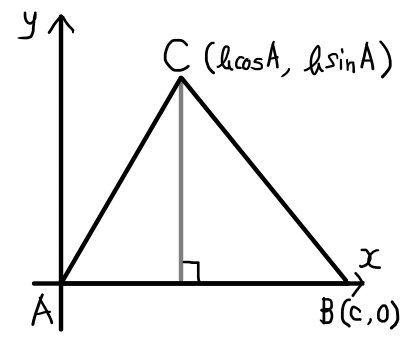
\bigtriangleup \mathrm{ABC}をxy直交座標の上に配置する.頂点\mathrm{A}の座標を(0,0),頂点\mathrm{B}の座標を(c,0)となるようにすると,頂点\mathrm{C}の座標を(b\cos{A}, b\sin{A})となる.ここで,頂点\mathrm{A}から辺\mathrm{BC}への垂線の足を\mathrm{H}とし,\bigtriangleup \mathrm{BCH}に着目すると,
\begin{aligned}
a^2 &= (c-b\cos{A})^2 + (b\sin{A})^2 \\
&= c^2 -2bc\cos{A} +b^2 \cos^2{A} + b^2 \sin^2{A} \\
&= c^2 + b^2(\cos^2{A} + \sin^2{A}) -2bc\cos{A} \\
&= c^2 + b^2 - 2bc\cos{A}
\end{aligned}
この式はAが鋭角,直角,鈍角のいずれの場合でも同様となる1鈍角の場合だけ少し操作が必要..
また,他の二つも同様に求めることができる.
最後に
別の記事でも言いましたが,三角比は数学Ⅰの中で最も慣れを要する概念です.ここで証明した定理を身につけるために,演習にも積極的に取り組みましょう.
