三角関数の加法定理とその証明

本記事では，三角関数の加法定理について説明したいと思います．

数学Ⅱで扱う三角関数の公式は，ほぼ加法定理から導き出せます．重要な定理ですので，丸暗記¹くだらない語呂合わせとか．に頼らず，しっかりと理解していきましょう．

加法定理(正弦，余弦)

初めに正弦(\sin)と余弦(\cos)の加法定理を紹介します．正弦，余弦の加法定理は以下の4つの式です．

三角関数の加法定理(正弦，余弦)
\begin{aligned} \sin(\alpha + \beta) &= \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}\\ \sin(\alpha - \beta) &= \sin{\alpha} \cos{\beta} - \cos{\alpha} \sin{\beta}\\ \cos(\alpha + \beta) &= \cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta}\\ \cos(\alpha - \beta) &= \cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta}\\ \end{aligned}

加法定理の証明

ではさっそく，加法定理を証明していきましょう．
数学Ⅱまでの知識ですと，\cos(\alpha - \beta)から証明することしかできません．証明された式を使って，他の式を証明するという流れになります．

それでは，4つの式が成り立つことを証明したいと思います．

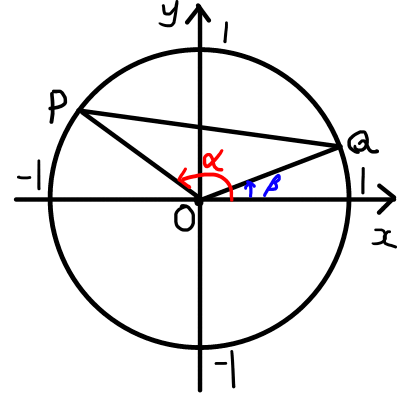
\cos(\alpha + \beta) = \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta} の証明．

\cos{(\alpha - \beta)} = \cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta} の\betaを- \betaに置き換えて，
\begin{aligned} \cos{\{ \alpha - (- \beta) \} } &= \cos{\alpha} \cos{(- \beta)} + \sin{\alpha} \sin{(- \beta)} \\ \cos{(\alpha + \beta)} &= \cos{\alpha} \cos{\beta} + \sin{\alpha}(- \sin{\beta}) \\ &= \cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta} \end{aligned}

\sin(\alpha + \beta) = \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} の証明．

\cos{(\alpha + \beta)} = \cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta} の\alphaを\alpha + \frac{\pi}{2}に置き換えて，
\begin{aligned} (左辺) &= \cos{ \left\{ \left ( \alpha + \frac{\pi}{2} \right) + \beta \right \} }\\ &= \cos{ \left \{ ( \alpha + \beta) + \frac{\pi}{2} \right \} } \\ &= - \sin(\alpha + \beta) \end{aligned}
\begin{aligned} (右辺) &= \cos{\left ( \alpha + \frac{\pi}{2} \right ) } \cos{\beta} - \sin{\left ( \alpha + \frac{\pi}{2} \right ) } \sin{\beta} \\ &= - \sin{\alpha} \cos{\beta} - \cos{\alpha} \sin{\beta} \end{aligned}
よって，
\begin{aligned} - \sin(\alpha + \beta) &= - \sin{\alpha} \cos{\beta} - \cos{\alpha} \sin{\beta} \\ \sin(\alpha + \beta) &= \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} \end{aligned}

\sin(\alpha - \beta) = \sin{\alpha} \cos{\beta} - \cos{\alpha} \sin{\beta} の証明．

\sin(\alpha + \beta) = \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta} の\betaを- \betaに置き換えて，
\begin{aligned} \sin{ (\alpha - \beta ) } &= \sin{\alpha} \cos{(- \beta)} + \cos{\alpha} \sin{(- \beta)} \\ &= \sin{\alpha} \cos{\beta} + \cos{\alpha}(- \sin{\beta}) \\ &= \sin{\alpha} \cos{\beta} - \cos{\alpha} \sin{\beta} \end{aligned}

加法定理(正接)

正接の加法定理は，正接しか出てこない形にすることができます．
正接の加法定理は以下の2つです．

三角関数の加法定理(正接)
\begin{aligned} \tan(\alpha + \beta) &= \frac{\tan{\alpha} + \tan{\beta}} {1 - \tan{\alpha} \tan{\beta}}\\ \tan(\alpha - \beta) &= \frac{\tan{\alpha} - \tan{\beta}} {1 + \tan{\alpha} \tan{\beta}}\\ \end{aligned}

これらの定理は，正弦，余弦の加法定理から証明することができます．

\begin{aligned} \tan(\alpha + \beta) &= \frac{\tan{\alpha} + \tan{\beta}} {1 - \tan{\alpha} \tan{\beta}} \end{aligned} の証明．

\begin{aligned} \tan(\alpha + \beta) &= \frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} \\ &= \frac{\sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta}} \\ &= \frac{\frac{\sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta}}}{\frac{\cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta}}} \\ &= \frac{\frac{\sin{\alpha} \cos{\beta}}{\cos{\alpha} \cos{\beta}} + \frac{\cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta}}}{\frac{\cos{\alpha} \cos{\beta}}{\cos{\alpha} \cos{\beta}} - \frac{\sin{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta}}} \\ &= \frac{\frac{\sin{\alpha}}{\cos{\alpha}} + \frac{\sin{\beta}}{\cos{\beta}}}{1 - \frac{\sin{\alpha}}{\cos{\alpha}} \cdot \frac{\sin{\beta}}{\cos{\beta}}} \\ &= \frac{\tan{\alpha} + \tan{\beta}} {1 - \tan{\alpha} \tan{\beta}} \end{aligned}

\begin{aligned} \tan(\alpha - \beta) &= \frac{\tan{\alpha} - \tan{\beta}} {1 + \tan{\alpha} \tan{\beta}} \end{aligned} の証明．

\begin{aligned} \tan(\alpha + \beta) &= \frac{\tan{\alpha} + \tan{\beta}} {1 - \tan{\alpha} \tan{\beta}} \end{aligned}の\betaを- \betaに置き換えて，
\begin{aligned} \tan(\alpha - \beta) &= \frac{\tan{\alpha} + \tan{ (- \beta)}} {1 - \tan{\alpha} \tan{(-\beta)}} \\ &= \frac{\tan{\alpha} - \tan{\beta}} {1 + \tan{\alpha} \tan{\beta}} \end{aligned}

演習問題

この節では，以前の三角比の記事で求めた，\frac{\pi}{12}(15^{\circ})や\frac{5}{12} \pi(75^{\circ})の三角関数の値を，加法定理を用いて求めてみましょう．

↓以前の三角比の記事↓

三角比の基礎　〜はじまりは直角三角形と相似〜

演習問題．
次の値を求めよ．

（1）\begin{aligned} \sin{\frac{\pi}{12}} \end{aligned}

（2）\begin{aligned} \cos{\frac{\pi}{12}} \end{aligned}

（3）\begin{aligned} \tan{\frac{\pi}{12}} \end{aligned}

（4）\begin{aligned} \sin{\frac{5}{12} \pi } \end{aligned}

（5）\begin{aligned} \sin{\frac{5}{12} \pi } \end{aligned}

（6）\begin{aligned} \sin{\frac{5}{12} \pi } \end{aligned}

解答例

（1）

\begin{aligned} \sin{\frac{\pi}{12}} &= \sin{\left( \frac{\pi}{3} - \frac{\pi}{4} \right)} \\ &= \sin{\frac{\pi}{3}} \cos{\frac{\pi}{4}} - \cos{\frac{\pi}{3}} \sin{\frac{\pi}{4}} \\ &= \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} - \frac{1}{2} \cdot \frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4} \\ &= \frac{\sqrt{6} - \sqrt{2}}{4} \end{aligned}

（2）

\begin{aligned} \cos{\frac{\pi}{12}} &= \cos{\left( \frac{\pi}{3} - \frac{\pi}{4} \right)} \\ &= \cos{\frac{\pi}{3}} \cos{\frac{\pi}{4}} + \sin{\frac{\pi}{3}} \sin{\frac{\pi}{4}} \\ &= \frac{1}{2} \cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} \\ &= \frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} \\ &= \frac{\sqrt{6} + \sqrt{2}}{4} \end{aligned}

（3）

\begin{aligned} \tan{\frac{\pi}{12}} &= \tan{\left( \frac{\pi}{3} - \frac{\pi}{4} \right)} \\ &= \frac{\tan{ \frac{\pi}{3}} - \tan{\frac{\pi}{4}}} {1 + \tan{ \frac{\pi}{3}} \tan{\frac{\pi}{4}}}\\ &= \frac{\sqrt{3} - 1}{1 + \sqrt{3}} \\ &= \frac{(\sqrt{3} - 1)^2}{(\sqrt{3} + 1)(\sqrt{3} - 1)} \\ &= \frac{4 - 2 \sqrt{3}}{2} \\ &= 2 - \sqrt{3} \end{aligned}

（4）

\begin{aligned} \sin{\frac{5}{12} \pi} &= \sin{\left( \frac{\pi}{4} + \frac{\pi}{6} \right)} \\ &= \sin{\frac{\pi}{4}} \cos{\frac{\pi}{6}} + \cos{\frac{\pi}{4}} \sin{\frac{\pi}{6}} \\ &= \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} \\ &= \frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} \\ &= \frac{\sqrt{6} + \sqrt{2}}{4} \end{aligned}

（5）

\begin{aligned} \cos{\frac{5}{12} \pi} &= \cos{\left( \frac{\pi}{4} + \frac{\pi}{6} \right)} \\ &= \cos{\frac{\pi}{4}} \cos{\frac{\pi}{6}} - \sin{\frac{\pi}{4}} \sin{\frac{\pi}{6}} \\ &= \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \cdot \frac{1}{2} \\ &= \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4} \\ &= \frac{\sqrt{6} - \sqrt{2}}{4} \end{aligned}

（3）

\begin{aligned} \tan{\frac{5}{12} \pi} &= \tan{\left( \frac{\pi}{4} + \frac{\pi}{6} \right)} \\ &= \frac{\tan{ \frac{\pi}{4}} + \tan{\frac{\pi}{6}}} {1 - \tan{ \frac{\pi}{4}} \tan{\frac{\pi}{6}}}\\ &= \frac{1 + \frac{\sqrt{3}}{3}}{1 - \frac{\sqrt{3}}{3}} \\ &= \frac{\frac{3+\sqrt{3}}{3}}{\frac{3-\sqrt{3}}{3}} \\ &= \frac{3 + \sqrt{3}}{3} \cdot \frac{3}{3 - \sqrt{3}} \\ &= \frac{3 + \sqrt{3}}{3 - \sqrt{3}} \\ &= \frac{(3 + \sqrt{3})^2}{(3 - \sqrt{3})(3 + \sqrt{3})} \\ &= \frac{12 + 6 \sqrt{3}}{6} \\ &= 2 + \sqrt{3} \end{aligned}

加法定理の思い出し方(図)

加法定理を思い出す方法をひとつ紹介したいと思います．もちろん妙な語呂合わせではありません．
図を使う方法です．Newton2022年2月号(2021年12月25日発売)でも解説記事がありました．

その方法なのですが，ものすごく丁寧に解説している方がいらっしゃいましたので，そちらの記事を紹介して終わりたいと思います³他の記事もしっかりしているのでオススメです．．

なかけんの数学ノート |【基本】図で理解する正弦・余弦の加法定理
https://math.nakaken88.com/textbook/basic-trigonometric-addition-formulas-with-picture/

　　

「勝手気ままに高校数学」シリーズ一覧へ