中線定理の証明
本記事では,中線定理(パッポスの定理)を2通りの方法で証明します.
中線定理(パッポスの定理)
\bigtriangleup \mathrm{ABC}において,辺\mathrm{BC}の中点を\mathrm{M}とするとき,以下の等式が成り立つ.
\mathrm{AB}^2 + \mathrm{AC}^2 = 2(\mathrm{AM}^2 + \mathrm{BM}^2)
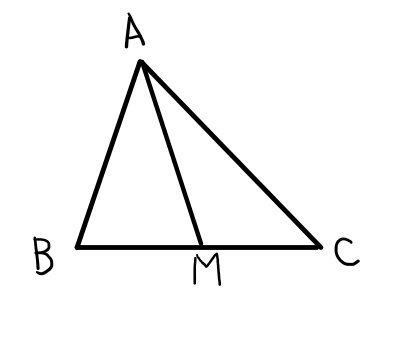
証明1(三角比を用いる)
\angle \mathrm{AMB} = \thetaとする.(\angle \mathrm{AMC} = 180^{\circ} - \theta)
\bigtriangleup \mathrm{ABM}に対して余弦定理を用いて,
\cos{\theta} = \frac{\mathrm{AM}^2 + \mathrm{BM}^2 - \mathrm{AB}^2}{2 \cdot \mathrm{AM} \cdot \mathrm{BM}}
同様に\bigtriangleup \mathrm{ACM}と余弦定理より,
\cos{(180^{\circ} -\theta)} = \frac{\mathrm{AM}^2 + \mathrm{CM}^2 - \mathrm{AC}^2}{2 \cdot \mathrm{AM} \cdot \mathrm{CM}}
\cos{(180^{\circ} - \theta)} = -\cos{\theta}なので,
\frac{\mathrm{AM}^2 + \mathrm{BM}^2 - \mathrm{AB}^2}{2 \cdot \mathrm{AM} \cdot \mathrm{BM}} = - \frac{\mathrm{AM}^2 + \mathrm{CM}^2 - \mathrm{AC}^2}{2 \cdot \mathrm{AM} \cdot \mathrm{CM}}
\mathrm{BM} = \mathrm{CM}より,
\begin{aligned}
\mathrm{AM}^2 + \mathrm{BM}^2 - \mathrm{AB}^2 &= -(\mathrm{AM}^2 + \mathrm{BM}^2 - \mathrm{AC}^2) \\
\mathrm{AB}^2 + \mathrm{AC}^2 &= 2(\mathrm{AM}^2 + \mathrm{BM}^2)
\end{aligned}
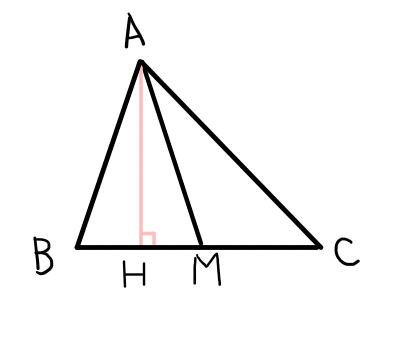
証明2(三平方の定理を用いる)
頂点\mathrm{A}から直線\mathrm{BC}に向かって垂線をおろし,その交点を\mathrm{H}とする.
\bigtriangleup \mathrm{ABH}と\bigtriangleup \mathrm{ACH}に関して,三平方の定理より,
\begin{aligned}
\mathrm{AB}^2 + \mathrm{AC}^2 &= (\mathrm{AH}^2 + \mathrm{BH}^2) + (\mathrm{AH}^2 + \mathrm{CH}^2) \\
&= 2\mathrm{AH}^2 + \mathrm{BH}^2 + \mathrm{CH}^2
\end{aligned}
ここで,
\mathrm{BH}^2 + \mathrm{CH}^2 = (\mathrm{BM} + \mathrm{MH})^2 + |\mathrm{CM} - \mathrm{MH}|^2
\mathrm{CM} = \mathrm{BM}なので,
\begin{aligned}
\mathrm{BH}^2 + \mathrm{CH}^2 &= (\mathrm{BM} + \mathrm{MH})^2 + |\mathrm{CM} - \mathrm{MH}|^2 \\
&= (\mathrm{BM} + \mathrm{MH})^2 + (\mathrm{BM} - \mathrm{MH})^2 \\
&= 2\mathrm{BM}^2 + 2\mathrm{MH}^2
\end{aligned}
よって,
\begin{aligned}
\mathrm{AB}^2 + \mathrm{AC}^2 &= 2\mathrm{AH}^2 + \mathrm{BH}^2 + \mathrm{CH}^2 \\
&= 2\mathrm{AH}^2 + 2\mathrm{BM}^2 + 2\mathrm{MH}^2 \\
&= 2(\mathrm{AH}^2 + \mathrm{MH}^2) + 2\mathrm{BM}^2 \\
&= 2(\mathrm{AM}^2 + \mathrm{BM}^2)
\end{aligned}