実数と無理数のお話

また，おかしな記事を書いてしまった．

さめのたなか（この記事の投稿直前）

実数と無理数について，取り留めのない話をします．

興味の無い方も，最後の問題だけは解いていってください！

実数の定義は難しい

実数の定義は難しいことです．

いくつかのWebサイト¹特に中高生向けのサイトでは，以下のような定義が見られます．

数直線上の点として表すことのできる数のことを実数という．

さて，この定義に問題を感じない人もいるでしょう．
しかし，よく考えてみてください．
「数直線」とはなんでしょうか？
数直線は，数の大小と点の左右の位置関係が一致するように，直線上の点と数を対応させたものです．
そして，上の定義（？）では，実数について言及しているので実数直線のことを言っているのでしょう．つまり，ここの数直線の定義でいう数とは実数のことを指します．

ここまでのお話をまとめると，
数直線は，実数を直線上の点と対応させたもので，
実数は，数直線上の点として表すことのできる数．
ん？堂々巡りしていますね．
「右とは左の反対のこと，左とは右の反対のこと」のようなトートロジーになっています．
これでは，定義できているとは言えません．

さて，実数の定義でよく見るものは以下のものでしょう．

有理数と無理数を合わせて実数という．

何も問題がないように見えますが，有理数，無理数の定義の仕方によっては，簡単に破綻してしまいます．

分数で表すことができる数を有理数という．
分数で表すことができない数を無理数という．

有理数，無理数の定義の中にある「数」とは何でしょうか？これはやはり実数のことなのです．「数」が実数より広い概念を示しているとすると，\frac{a+bi}{c+di} 　(iは虚数単位)²複素数を知らない方は，i^2=-1であること，iは実数でないことを理解すると話の筋が分かるかと思います．もOKになってしまうので，定義として破綻してしまいます．「数」を実数だとすると，実数の定義と合わせて，これも堂々巡りになってしまいます．

このように，実数の定義はとても難しいものです．そのため，まともな参考書や中高生向けWebページほど，「定義」という言葉を避けて説明をしています．数ある参考書の中で，かなり隙の少ない定義をしているのが，『総合的研究』の以下の定義です³これも無理数の性質といいたいですが．．

実数とは，小数（すなわち有限小数または無限小数）で表せる数

長岡亮介『総合的研究　数学Ⅰ+A』 旺分社 60ページ

実数の定義は難しいですが，大学の解析学では，実数が持つ性質である「連続性」⁴びっしり隙間なく詰まっているイメージが重要になってくるため，最初に実数の定義を行うことがあります⁵実数を作ることもあります．丁寧な場合だと，自然数から整数を構成して，整数から有理数を構成して，有理数から実数を構成する，なんてこともやります．なお，全ての数学的概念を集合論から始めるために，(空)集合から自然数を構成することもありますが，それを経験する人は少数でしょう．また，実数を公理として与え，そこから自然数を構成する方法もあります．一体どのように定義するのか，大学に入ってからのお楽しみです．

ここまで書いておきながら言いにくいことですが，中高校生の間は実数の定義にとらわれず，有理数と無理数から成ることを覚えておき，あとは何となくのイメージを持っていればOKです．

無理数のイメージ

無理数は英語だとirrational numberといい，直訳すると「比で表せない数」です．つまり，分数で表せない数となります．また，無理数は無限小数で表される数ともいえます．

と言われてもナンノコッチャな人も多いでしょう．

無理数の例として正の平方根である\sqrt{2}や\sqrt{3}，円周率の\pi などが挙げられます．他にも沢山ある，というよりもその辺りに無数にあるのですが⁶そもそも有理数より無理数の方が多い．，なかなか掴みどころがありません．

元から掴みどころが無いものですから，その演算となると，さらにイメージが難しいはずです．
例えば「無理数で割る」とは，どういうことでしょうか．イメージできましたか？
「負の数の掛け算」や「分数の割り算」のイメージが湧かないという声は聞こえますが，\frac{\sqrt{3}}{\sqrt{2}}のイメージが湧かないという声が聞こえないのは何故でしょうか．高校生にもなると，代数的演算への信頼性と言いましょうか，そういった類の直感が格段に鋭くなるのでしょうか．それならば，こんなにも抽象的なものを自然と扱えるようになったと喜びましょう！

失礼，話が逸れてしまいました．

ここでは，もはや疑問に思わないであろう，分母の有理化についてお話ししたいと思います．
分母の有理化は，分数の分母と分子に同じ数を掛けても元の分数と変わらない性質を利用しています．通分などで使われる性質です．この性質を視覚的に捉えてみましょう．

まず，分母と分子が整数の場合をイメージしてみましょう．
\frac{1}{5} = \frac{3}{15}を図で表すとどうなるでしょうか．

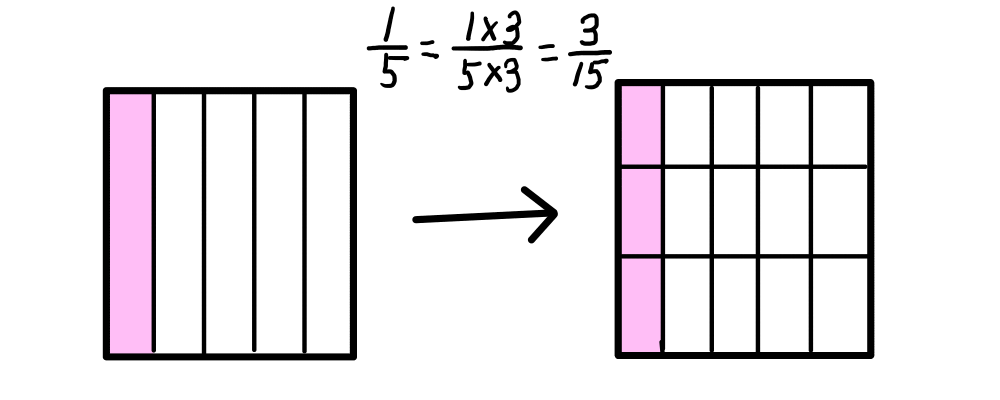
上の図の通り，簡単に図示できました．

では，次の有理化の場合はどうでしょうか．

\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3} \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{6}}{2}

うーむ．まず\frac{\sqrt{3}}{\sqrt{2}}の図が難しいですね．
下の図の左側のような感じでしょうか．一辺が\sqrt{2}，面積が\sqrt{3}の直方体の，もう一方の辺の長さです．ちょっと強引な気がします．

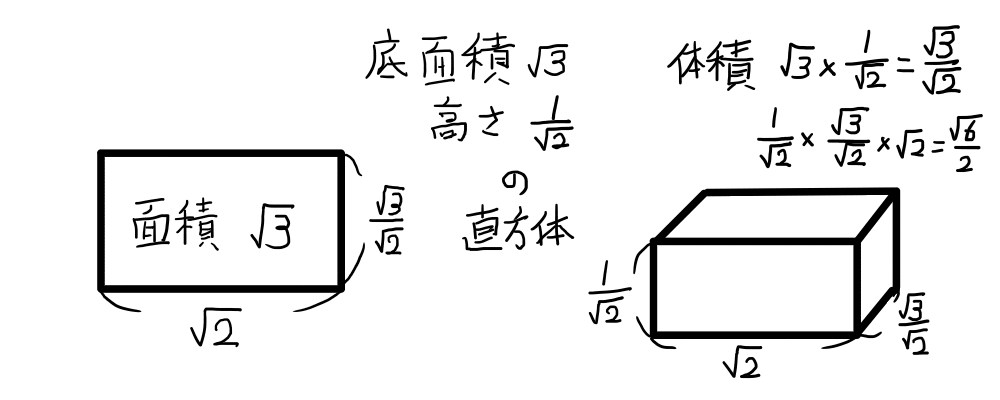
有理化については，上の右側の図でどうでしょうか．有理化を体積の計算順序の違いとして図示(?)してみました．

\frac{\sqrt{3}}{\sqrt{2}} = (\sqrt{2} \times \frac{1}{\sqrt{2}}) \times \frac{\sqrt{3}}{\sqrt{2}}  = \sqrt{2} \times (\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{\sqrt{2}}) = \frac{\sqrt{6}}{2}

なんだか，すでに整理されているものを，いたずらにかき回している気がします．

この話はここで終わり！

平方根を数直線上にプロットする

無理数の代表的な数である，正の平方根\sqrt{n}を数直線上にプロットしてみようと思います．せっかくなので，フリーハンドで，\sqrt{n}の近似値を計算することなく，プロットしてみましょう．遊びというものは，多少の制限があった方が面白いものです．

ここからは，私ならこう書くという一例です．

初めにxy座標を用意し，そこにy=x^2のグラフをできるだけ綺麗に描きます．

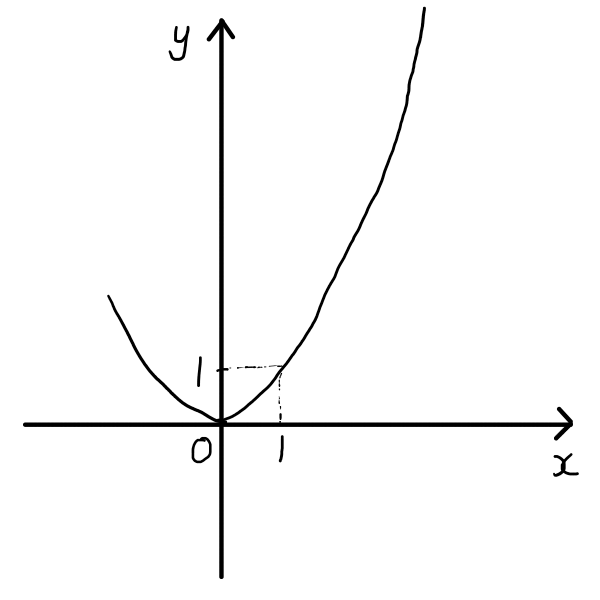
x軸に\sqrt{n}の点を描きましょう．第1象限に注目します．
まずは，\sqrt{2}の点を打ちます．y=2のとき，つまり2=x^2のとき，xがとりうる正の値は，x= \sqrt{2}です．(x,y)= (0,2)から，x軸に水平な線を引き，グラフと交わったところからx軸に向かって垂線を下ろします．その線とx軸の交点が(x,y)= ( \sqrt{2} ,0)です．

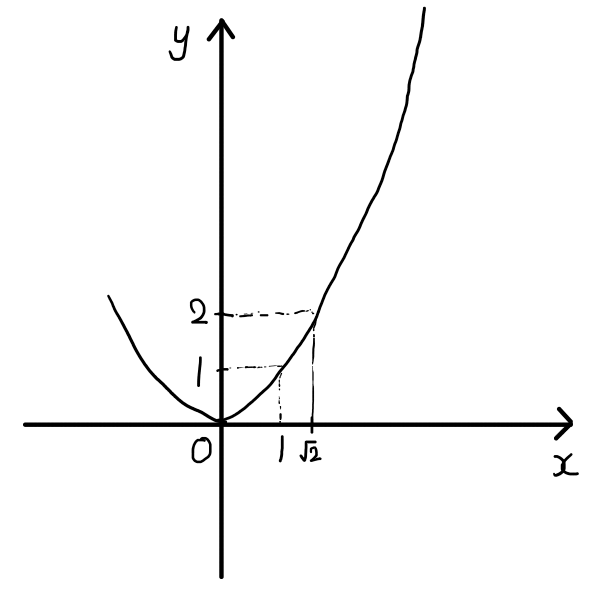
同様に，n = 3, 4, 5, \cdots と続けます．

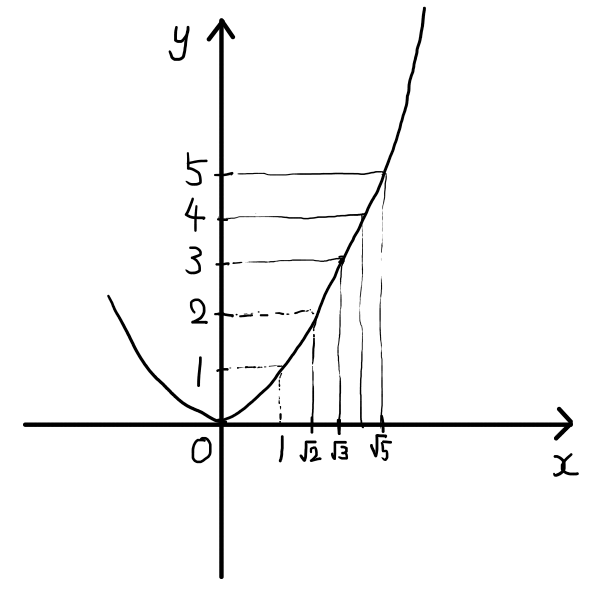
手法としては，以上となります．

さて，こうして図を眺めてみると，nが大きくなるにつれて，\sqrt{n}の間隔が狭くなっているように見えます．\sqrt{n+1} - \sqrt{n} > \sqrt{n+2} - \sqrt{n+1}が成り立ちそうですね．

それでは最後に，この不等式の証明を演習問題として終わりたいと思います．

（追記）条件を厳しくしてみました．

xが0以上の実数のとき，正の定数\epsilonに関して，次の式が成り立つことを証明せよ．
\sqrt{x + \epsilon} - \sqrt{x} > \sqrt{x + 2\epsilon} - \sqrt{x + \epsilon}

ヒント⁷a > b ならば \sqrt{a} > \sqrt{b}
この命題の証明が思いつかない人は，この命題の証明もすること．それと不等式の操作について勉強し直すこと．

ヒント2⁸\sqrt{n+1} - \sqrt{n} = \frac{1}{\sqrt{n+1} + \sqrt{n}}

「勝手気ままに高校数学」シリーズ一覧へ