1-3. 因数分解の基礎

本記事の目標：
因数分解について理解し，素早く計算できるようにする．

　前回は展開について学習しました．展開とは，複数の整式の掛け算を計算して，ひとつの整式にすることです．今回学習する因数分解では，展開とは逆に，整式を複数の整式の積に変形します．因数分解の過程はパズルに近いので，楽しく学習しましょう．

因数分解とは

　因数分解とは，整式を複数の整式の積の形に変形することです．文章で書くと複雑なので，例を見てみましょう．

x^2 + 8x + 15 = (x + 5) (x + 3)

x^2 - x - 12 = (x - 4) (x + 3)

6x^2 + 5x - 6 = (3x - 2)(2x+ 3)

すごく大雑把に言うと，展開の逆の操作をしています．試しに，右辺を展開して左辺になるか確認してみましょう．

　高校数学で「因数分解せよ」と言われた場合は，係数が有理数の範囲で可能な限り分解します．つまり， $x^2 - 4 = (x + 2) (x - 2)$ は必要な分解ですが， $x^2 - 2 = (x + \sqrt{2}) (x - \sqrt{2})$ と分解する必要はありません．「分解前に根号が無い式は，分解後も根号が出ないようにしましょう」というわけです．

　ちなみに，因数分解という言葉の「因数」とは何かと疑問に思う人もいるでしょう．大雑把にいうと，因数とは約数のことです．正の整数を素数の積に分解する，素因数分解なんて言葉もありますよね．これも約数に分解していると考えると，「因数」という言葉が何となく分かるかもしれません．

共通因数を見つけよう！

　因数分解をするうえで一番最初に着目することは，共通因数を見つけることです．共通因数とは，全ての項に共通の約数（みたいなもの）だと思ってください．次の式を見てみましょう．

a^2 + ab + ca

全ての項に $a$ が含まれています．この式は，分配法則の逆を使って以下のように分解することができます．

a^2 + ab + ca = a(a + b + c)

このように共通因数を式の外に出す操作のことを，「共通因数をくくり出す」といいます．

　それでは，共通因数をくくり出す例題をいくつか解いてみましょう．

例題1．
次の式を因数分解をせよ．
(1) $- 2a - 2b - 2c$
(2) $-4x^2 + 8xy - 4zx$
(3) $12a^4b - 6a^3b^2 + 9a^2b^3$
(4) $3x^2y + 9x^2y^2 - 6xy^3$
(5) $231a^2bc - 84ab^2c - 126abc^2 + 63abcd$

例題1の解答．

解答を読む

例題1の解答．
(1)
$-2a -2b -2c = -2(a + b + c)$

(2)
$-4x^2 + 8xy - 4xz = -4x(x -2y + z)$

(3)
$12a^4b - 6a^3b^2 + 9a^2b^3 = 3a^2b(4a^2 - 2ab + 3b^2)$

(4)
$3x^2y + 9x^2y^2 - 6xy^3 = 3xy(x + 3xy -2y^2)$

(5)
$231a^2bc - 84ab^2c - 126abc^2 + 63abcd = 21abc(11a - 4b - 6c + 3d)$

2次の因数分解の公式

　次に2次の因数分解の公式を紹介します．

2次の因数分解の公式．
$a^2 + 2ab + b^2 = (a + b)^2$

$a^2 - 2ab + b^2 = (a - b)^2$

$a^2 - b^2 = (a + b)(a - b)$

$x^2 + (a + b)x + ab = (x + a)(x + b)$

$acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)$

展開公式の右辺と左辺を入れ替えただけです．上3つは公式に当てはめるだけで因数分解できます．下2つの公式は適切な $a, b, c, d$ を見つけなければなりません．下2つの公式を使いこなすテクニックとして，本記事ではたすき掛けを紹介します．たすき掛けに関しては後半の節で紹介したいと思います．

　上3つの公式を当てはめる例を紹介します．

4x^2 + 4xy + y^2 = (2x)^2 + 2(2x)y + y^2 = (2x + y)^2

元の公式の $a$ に当てはまるのが $2x$ ， $b$ に当てはまるのが $y$ です．

9x^2 - 12xy + 4y^2 = (3x)^2 - 2(3x)(2y) + (2y)^2 = (3x - 2y)^2

9a^2 - 25 b^2 = (3a)^2 - (5b)^2 = (3a + 5b)(3a - 5b)

例題2．
次の式を因数分解せよ．
(1) $4x^2 + 4xy + y^2$
(2) $9a^2 - 6ab + b^2$
(3) $16x^2 -72x + 81$
(4) $9x^2 - 4y^2$
(5) $81a^2 -121b^2$

例題2の解答と解説．

解答と解説を読む

例題2の解答．
(1) $4x^2 + 4xy + y^2 = (2x + y)^2$
(2) $9a^2 - 6ab + b^2 = (3a - b)^2$
(3) $16x^2 -72x + 81 = (4x - 9)^2$
(4) $9x^2 - 4y^2 = (3x + 2y)(3x - 2y)$
(5) $81a^2 -121b^2 = (9a + 11b)(9a - 11b)$

3次の因数分解の公式

　次に3次の因数分解の公式を紹介します．

3次の因数分解の公式．
$a^3 + 3a^2b + 3ab^2 + b^3 = (a + b)^3$

$a^3 - 3a^2b + 3ab^2 - b^3 = (a - b)^3$

$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$

$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$

$a^3 + b^3 + c^3 -3abc = (a + b + c)(a^2 + b^2 + c^2 - ab - bc - ca)$

　3次の因数分解の公式で最も注意すべきは，一番下の公式です． $c$ にあたる部分に数が入ることが多く，公式がそのまま使えることに気付きにくい場合があります．例えば，

x^3 + y^3 + 6xy - 8

のような式が挙げられます．この式は例題3で因数分解してみましょう．

この説の最後に，他の因数分解の公式が当てはまる式の例を挙げたいと思います．

x^3 + 6 x^2 + 12 x + 8 = (x)^3 + 3(x)^2 \cdot 2 + 3x \cdot 2^2 + 2^3 = (x + 2)^3

27x^3 - 64 = (3x)^3 - 4^3 = (3x - 4)(9x^2 + 12x + 16)

例題3．
次の式を因数分解せよ．
(1) $8x^3 + 12x^2y + 6xy^2 + y^3$
(2) $27a^3 - 27a^2b + 9ab^2 - b^3$
(3) $27x^3 - 108x^2 + 144x - 64$
(4) $27x^3 + 8y^3$
(5) $27a^3 - 64b^3$
(6) $x^3 + y^3 + 6xy - 8$

例題3の解答．

解答を読む

例題3の解答．
(1) $8x^3 + 12x^2y + 6xy^2 + y^3 = (2x + y)^3$

(2) $27a^3 - 27a^2b + 9ab^2 - b^3 = (3a - b)^3$

(3) $27x^3 - 108x^2 + 144x - 64 = (3x - 4)^3$

(4) $27x^3 + 8y^3 = (3x + 2y)(9x^2 - 6xy + 4y^2)$

(5) $27a^3 - 64b^3 = (3a - 4b)(9a^2 + 12ab + 16b^2)$

(6) $x^3 + y^3 + 6xy - 8 = (x)^3 + y^3 + (-2)^3 -3 xy(-2) = (x + y - 2)(x^2 + y^2 - xy + 2x + 2y + 4)$

たすき掛けをマスターしよう！

　さて，ここで2次の因数分解の公式に戻ります．ここでは，次の2つの公式を使いこなせるようにします．

2次の因数分解の公式．
$x^2 + (a + b)x + ab = (x + a)(x + b)$

$acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)$

　まずは， $x^2 + (a + b)x + ab = (x + a)(x + b)$ を使いこなせるようになりましょう．以下に因数分解の例を挙げます．

x^2 + 8x + 12 = (x + 6)(x + 2)

この例を公式と見比べてみます．

$x^2 + (a + b)x + ab = (x + a)(x + b)$
$x^2 + 8x + 12 = (x + 6)(x + 2)$

公式における $a$ は $6$ ， $b$ は $2$ となります．この， $a$ と $b$ にあたる数を見つけることが大変です． $ab = 12$ と $a + b = 8$ の両方を満たす必要があります． $12$ は，
$1$ と $12$
$-1$ と $-12$
$2$ と $6$
$-2$ と $-6$
$3$ と $4$
$-3$ と $-4$
$4$ と $3$
$-4$ と $-3$
$6$ と $2$
$-6$ と $-2$
$12$ と $1$
$-12$ と $-1$
の12通りの分解の仕方があります．この中から，足して $8$ になるのは， $2$ と $6$ もしくは， $6$ と $2$ だけです．つまり公式の $a$ ， $b$ に当てはまるのはこの2通りだけになります．

　この分解を上手く見つけるテクニックがたすき掛けです．

　 $acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)$ の場合，たすき掛けはズバリ以下のような図をかいて，解を見つけるテクニックです！

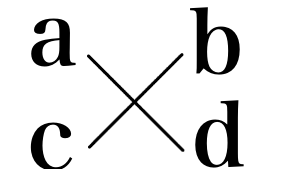
最初のうちは，もう少し色々と書いても良いでしょう(下の図)．

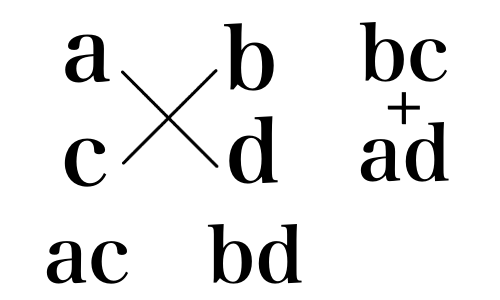
さて，この図の見方を覚えていきましょう．

まずは， $ac$ と $bd$ を分解したものを縦に書きます．

斜めに書いてある，線で繋がれた数を掛け合わせます．

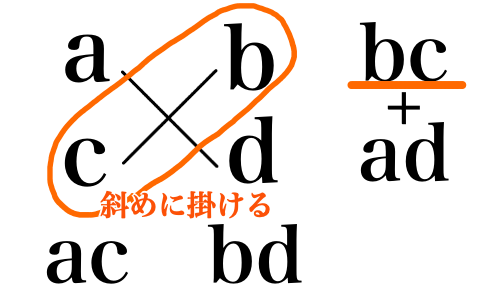
もう片方側も．

斜めに掛けた数を足して $ad + bc$ になるか確認しましょう．

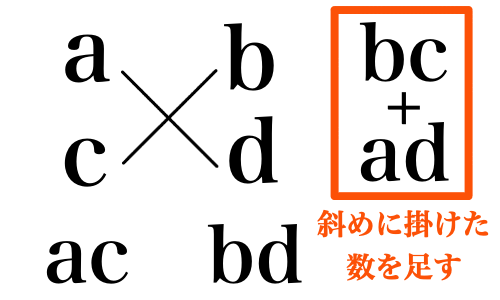
　　斜めに掛ける部分が，たすきのようなので，たすき掛けと呼ばれるのでしょう．

　まずはたすき掛け入門として $x^2 + (a + b)x + ab = (x + a)(x + b)$ をたすき掛けで求めてみましょう．下のような図を作っていこうと思います．

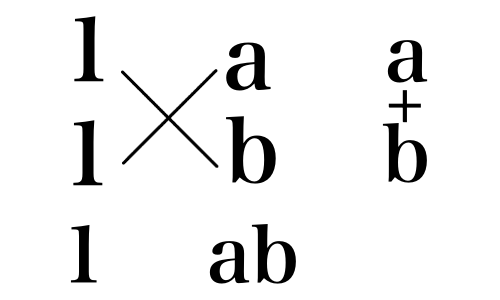
　実際の式でたすき掛けの図を書いてみましょう．

　 $x^2 + 7x + 12$ を因数分解してみます． $12$ をどのように分解するかがポイントです． $2$ と $6$ に分解してみましょう．たすき掛けの図は以下のようになります．

$a + b$ が $7$ でないため誤りです．

次に $3$ と $4$ に分解してみます．

正しい分解方法は $3$ と $4$ のようです．よって $x^2 + 7x + 12 = (x + 3)(x + 4)$ となります．

　それでは例題を解いてみましょう．

例題4．
次の式を因数分解せよ．
(1) $x^2 + 4x + 3$
(2) $x^2 + 8x + 15$
(3) $x^2 + 12x + 20$
(4) $x^2 - 10x + 24$
(5) $x^2 - 3x - 18$
(6) $x^2 + x - 20$
(7) $x^2 - x - 12$
(8) $x^2 + 3x - 28$

例題4の解答．

解答を読む

例題4の解答．
(1) $x^2 + 4x + 3 = (x + 1)(x + 3)$

(2) $x^2 + 8x + 15 = (x + 3)(x + 5)$

(3) $x^2 + 12x + 20 = (x + 2)(x + 10)$

(4) $x^2 - 10x + 24 = (x - 4)(x - 6)$

(5) $x^2 - 3x - 18 = (x + 3)(x - 6)$

(6) $x^2 + x - 20 = (x + 5)(x - 4)$

(7) $x^2 - x - 12 = (x + 3)(x - 4)$

(8) $x^2 + 3x - 28 = (x - 4)(x + 7)$

たすき掛けは以下のようになります．

(1)
$x^2 + 4x + 3 = (x + 1)(x + 3)$

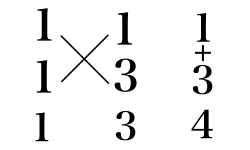
(2)
$x^2 + 8x + 15 = (x + 3)(x + 5)$

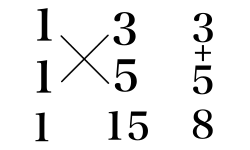
(3)
$x^2 + 12x + 20 = (x + 2)(x + 10)$

(4)
$x^2 - 10x + 24 = (x - 4)(x - 6)$

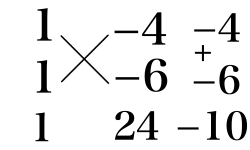
(5)
$x^2 - 3x - 18 = (x + 3)(x - 6)$

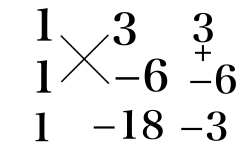
(6)
$x^2 + x - 20 = (x + 5)(x - 4)$

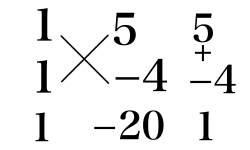
あ，そういえば．
たすき掛けの右側の＋は慣れてきたら省略しても構いません．何なら，下に書いてある掛け算の結果や，足し算の結果を省いても問題ありません．たすき掛けはただの道具なので，使いやすさを優先してアレンジしていきましょう．

(7)
$x^2 - x - 12 = (x + 3)(x - 4)$

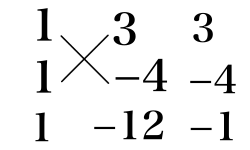
(8)
$x^2 + 3x - 28 = (x - 4)(x + 7)$

　次に， $acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)$ の公式をたすき掛けで使ってみましょう．

2x^2 + x - 6

上の式を因数分解してみましょう．たすき掛けで $a, b, c, d$ を見つけます．

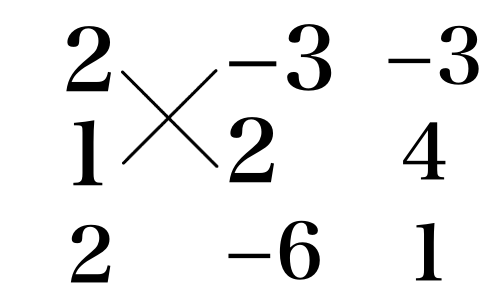
したがって，

2x^2 + x - 6 = (2x - 3)(x + 2)

となります．

たすき掛けは「習うより慣れろ」なテクニックなので，問題をガンガン解いて慣れていきましょう．

例題5．
次の式を因数分解せよ．
(1) $6x^2 + 5x - 6$
(2) $2x^2 + 5x + 2$
(3) $6x^2 + x - 12$
(4) $3x^2 + 8x - 3$
(5) $6x^2 + 17x - 14$
(6) $20x^2 + x - 1$
(7) $6x^2 - x - 15$
(8) $3x^2 - x - 10$

例題5の解答．

解答を読む

例題5の解答．
(1) $6x^2 + 5x - 6 = (2x + 3)(3x - 2)$

(2) $2x^2 + 5x + 2 = (2x+1)(x + 2)$

(3) $6x^2 + x - 12 = (2x + 3)(3x - 4)$

(4) $3x^2 + 8x - 3 = (x + 3)(3x - 1)$

(5) $6x^2 + 17x - 14 = (3x - 2)(2x + 7)$

(6) $20x^2 + x - 1 = (5x - 1)(4x + 1)$

(7) $6x^2 - x - 15 = (2x + 3)(3x - 5)$

(8) $3x^2 - x - 10 = (3x + 5)(x - 2)$

(1)〜(4) のたすき掛けを載せておきます．

(1)
$6x^2 + 5x - 6 = (2x + 3)(3x - 2)$

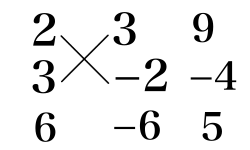
(2)
$2x^2 + 5x + 2 = (2x+1)(x + 2)$

(3)
$6x^2 + x - 12 = (2x + 3)(3x - 4)$

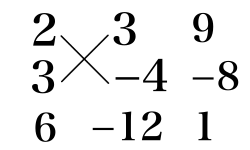
(4)
$3x^2 + 8x - 3 = (x + 3)(3x - 1)$

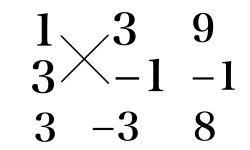
たすき掛け応用編

　たすき掛けで解ける因数分解の問題の応用編です．以下の式を因数分解してみましょう．

6x^2 + 11xy + 2x + 3y^2 - 4y + 4

まずは， $x$ に着目します．すると定数項が $3y^2 - 4y + 4$ であることがわかります． $x$ に着目したときの定数項を， $y$ で因数分解できそうです．試しに因数分解してみましょう．

3y^2 - 4y + 4 = (3y + 2)(y - 2)

ここで元の式に戻りましょう． $x$ で式をまとめます．

6x^2 + 11xy + 2x + 3y^2 - 4y + 4 \\ = 6x^2 + 11xy + 2x + (3y + 2)(y - 2) \\ = 6x^2 + (11y + 2)x + (3y + 2)(y - 2)

おや？何となく因数分解の公式 $acx^2 + (ad + bc)x + bd = (ax + b)(cx + d)$ が使えそうです．早速たすき掛けをしてみましょう．

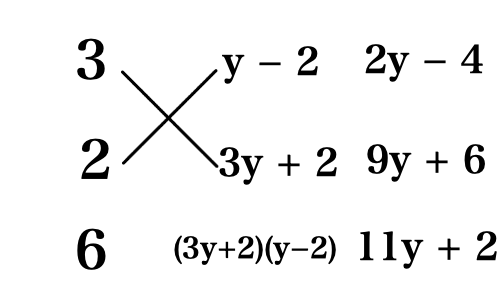
6x^2 + 11xy + 2x + 3y^2 - 4y + 4 \\ = 6x^2 + 11xy + 2x + (3y + 2)(y - 2) \\ = 6x^2 + (11y + 2)x + (3y + 2)(y - 2) \\ = (3x + y - 2)(2x + 3y + 2)

というわけで因数分解ができました．

　もし，「 $x$ に着目する」という言葉がわからない人は，以下の記事をご参照ください．

[演習問題] 1-1. 単項式，多項式，整式

例題6．
次の式を因数分解せよ．
(1) $2x^2 + 7xy - 7x + 6y^2 - 11y + 3$
(2) $3x^2 + 3xy - 14x - 6y^2 + 17y - 5$

例題6の解答．

解答を読む

例題6の解答．
(1)
$2x^2 + 7xy - 7x + 6y^2 - 11y + 3 \\ = 2x^2 + (7y - 7)x + (2y - 3)(3y - 1) \\ = (x + 2y - 3)(2x + 3y - 1)$

(2)
$3x^2 + 3xy - 14x - 6y^2 + 17y - 5 \\ = 3x^2 + (3y - 14)x - (6y^2 -17y + 5) \\ = 3x^2 + (3y - 14)x - (2y - 5)(3y - 1) \\ = (x + 2y - 5) \{3x - (3y - 1) \} \\ = (x + 2y - 5)(3x - 3y + 1)$

因数分解応用編

　式の次数が異様に高いときは，分解した後に，さらに因数分解できないか考えることが重要です．例えば，次の式を因数分解してみましょう．2行目で止めてしまわないように気をつけましょう．

x^4 - y^4 \\ = (x^2 + y^2)(x^2 - y^2) \\ = (x^2 + y^2)(x + y)(x - y)

　さらに次の因数分解を見てみましょう．

x^4 + 4 \\ = x^4 + 4x^2 + 4 - 4x^2 \\ = (x^2 + 2)^2 - 4x^2 \\ = (x^2 + 2x + 2)(x^2 - 2x + 2)

この手の問題では，何とかして $a^2 - b^2 = (a + b)(a - b)$ の公式を使える形にするのがポイントです．

例題7．
次の式を因数分解せよ．
(1) $x^6 - y^6$
(2) $x^4 - 5x^2 + 4$

例題7の解答．

解答を読む

例題7の解答．
(1)
$x^6 - y^6 \\ = (x^3 + y^3)(x^3 - y^3) \\ = (x + y)(x^2 - xy + y^2)(x - y)(x^2 + xy + y^2)$

(2)
$x^4 - 5x^2 + 4 \\ = (x^4 - 4x^2 + 4) - x^2 \\ = (x^2 - 2)^2 - x^2 \\ = (x^2 + x - 2)(x^2 - x - 2)$

因数分解のコツ

　この記事では，難解な因数分解は少ししか取り扱いませんでした．最後に，難解そうな因数分解の問題を上手く解くためのコツを3つ紹介したいと思います．

共通因数でくくる
因数分解の公式が使えないか考える
次数の低い文字で式をまとめる

全てのコツが大切です．どのコツが重要になるか，どの順番でコツを使うことになるか，式によって全く異なります．

　特に3つ目のコツ「次数の低い文字で式をまとめる」は，使いこなせると因数分解が一気に得意になると思います．例題8でこのコツの強力さを体感してみてください．

コラム：コツなんて関係なかった

コラムを読む

因数分解のコツを紹介しましたが，そんなものを超越した解き方も存在します．

$(a + b + c)^3 - a^3 - b^3 - c^3$ の因数分解を，先ほどのコツの不使用はもちろん，計算をせずに解いています．以下に詳細を書いているので，興味がある人は記事を読んでみてください．

ある因数分解の問題を計算なしで解く過程をアニメーションにしてみた

例題8．
次の式を因数分解せよ．
(1) $a^2 + ab + ac + bc$
(2) $x^2 + y^2 + 2xy + yz + zx$

例題8の解答．

解答を読む

例題8の解答．
(1)
次数の低い $b$ か $c$ でまとめてみましょう．
$a^2 + ab + ac + bc \\ = a^2 + ab + c(a + b) \\ = a(a + b) + c(a + b) \\ = (a + b)(a + b)$

(2)
最も次数の低い $z$ で式をまとめてみましょう．
$x^2 + y^2 + 2xy + yz + zx \\ = x^2 + y^2 + 2xy + z(x + y) \\ = (x + y)^2 + z(x + y) \\ = (x + y)(x + y + z)$

まとめ

　この記事では，因数分解を学習しました．因数分解とは，式を整式同士の積の形に分解する操作のことです．基本的な因数分解については，今後の単元でも必要になります．演習問題を解いて，しっかり身につけておくべきです．

　また，工夫が必要な因数分解の問題もあります．様々な因数分解の問題に取り組んでみましょう．難しい因数分解の問題は，パズルのような要素があります．新しい工夫のパターンを学びながら，楽しんで演習問題を解きましょう．

因数分解の早さや正確さに自信がない人は，演習問題を何度もこなして実力をつけましょう．
因数分解の演習ページは，2ページ用意しました．ご活用ください．

　次回は，これまでの文字式の学習から一転して，「数」について学習します．

《PR》

因数分解とは

共通因数を見つけよう！

2次の因数分解の公式

3次の因数分解の公式

たすき掛けをマスターしよう！

たすき掛け応用編

因数分解応用編

因数分解のコツ

まとめ

関連ページ