本記事の目標:
実数,有理数,無理数について理解する.
前回までは,展開や因数分解といった,文字の入った式の操作を学習しました.
今回は前回までとはがらりと変わり,「数」に注目します.具体的に扱う内容は以下の通りです.
- 実数,有理数,無理数とは何か
- 循環小数の分数への変換
- 数直線と絶対値
有理数,無理数,実数とは
自然数と整数についてはすでにご存知でしょう.自然数は,正の整数のこと示す場合もありますし,正の整数と 0 を表すことがあります.自然数に 0 を含めるかどうかは,その都度説明したいと思います.
有理数とは,以下のように整数の分数1整数の比で表せる数のことです.
\frac{(整数)}{(整数)}有理数は小数を使って説明することもできます.小数を使って有理数を説明すると,有限小数,または,循環する無限小数ということができます.
有限小数とは,0.75 のように,小数点以下の数に限りがある小数のことです.
無限小数は小数点以下に限りがなく,小数点以下が無限に続いていきます.例えば,\frac{1}{3} = 0.3333333 \cdots \cdots のような形です.
\frac{1}{3} = 0.3333333 \cdots \cdots のように,途中から同じ数字が繰り返される無限小数のことを循環小数といいます.\frac{1}{3} = 0.3333333 \cdots \cdots の場合,3 が繰り返されています.他にも \frac{1}{7} の場合,\frac{1}{7} = 0.142857142857142857 \cdots \cdots というふうに 142857 の繰り返しになります.循環小数は,循環する部分の最初と最後の数の上に,黒い点「・」を書いて,以下のように表記します.
\frac{1}{3} = 0.\dot{3}\\
\\
\frac{1}{7} = 0.\dot{1}4285\dot{7} \\
0.\dot{3} は 0.3333333 \cdots \cdots を意味しています.0.\dot{1}4285\dot{7} は 0.142857142857142857 \cdots \cdots です.
すべての有理数は,整数の分数2整数の比で表すことができ,また,有限小数3ここでは整数も有限小数に含めることにしますか循環小数で表すことができます.
例題1.
次の分数を小数にせよ.また循環小数は,「・」を使った表記で表せ.
(1) \begin{aligned} \frac{1}{4} \end{aligned}
(2) \begin{aligned} \frac{1}{6} \end{aligned}
(3) \begin{aligned} \frac{1}{13} \end{aligned}
例題1の解答.
例題1の解答.
(1) \begin{aligned} \frac{1}{4} = 0.25\end{aligned}
(2) \begin{aligned} \frac{1}{6} = 0.1\dot{6} \end{aligned}
(3) \begin{aligned} \frac{1}{13} = 0.\dot{0}7692\dot{3} \end{aligned}
無理数は,循環しない無限小数のことです.例えば,円周率の \pi は無理数です.循環することなく,無限に小数点以下が続きます.
有理数と無理数を合わせて,実数といいます.
実数,無理数,有理数,整数,自然数の関係を図にすると以下のようになります.
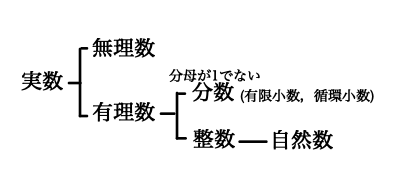
上の図は関係性が分かりにくい部分があるため,以下のような図で表すのも良いでしょう.

この図で重要なことは.
- 整数は有理数に含まれている4「含む」「含まれる」という言葉の正確な定義は,次の単元である「集合と論理」でご確認ください.
- 自然数は整数に含まれている
- 有理数でない実数は無理数
- 無理数でない実数は有理数
ということです.
コラム:自然数は幼児でも理解できる!?
数の概念は,どのように生まれてきたのでしょうか.実は新生児でも小さな自然数や量の大小が分かります.また,5ヶ月ほどの乳児は,小さな自然数の足し算や引き算が分かります.
乳児に小さな自然数の計算ができることを示す実験を挙げます.
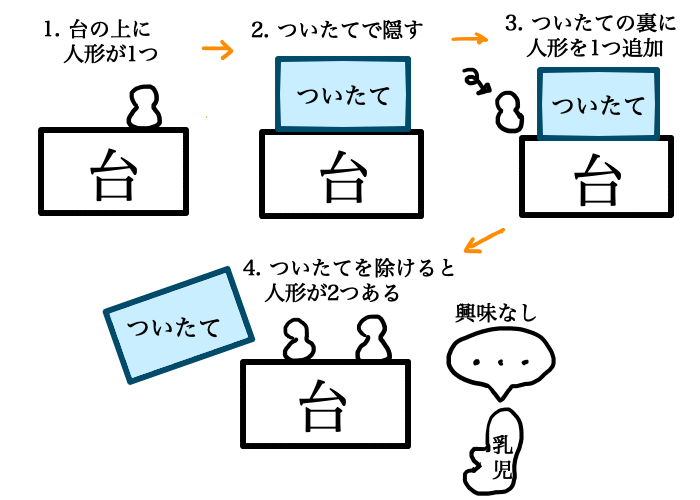
まずは,実験の初期状況から見てみましょう.台の上に人形が1体あります.その台には,「ついたて」が用意されており,乳児から台の上を隠すことができます.
ひとつ目の実験では,ついたての上に1体の人形を置きます.そして,ついたてで台の上を隠し,ついたての後ろへ,人形を1体,追加で台の上に置きます.このとき,台の横からついたての後ろに,もう1体の人形を置いている様子を,乳児に見せるようにします.そうすると,台の上の人形は2体になりますね.
被験者の乳児の目線で,状況を整理しましょう.ついたてで隠されているため,台の上の人形の数を知りませんが,ついたてで隠される前に1体の人形があり,ついたてで隠された状態でもう1体追加されたことを知っています.
ここでついたてを取り除きます.台の上には人形が2体います.我々にとっては,当たり前のことです.ところが,この結果は乳児にとっても当たり前のことらしく,乳児は台の上の人形に興味を示しません.
ここまでがひとつ目の実験です.
次に,ふたつ目の実験ですが,ひとつ目の実験と途中まで同じです.台の上に1体の人形があり,ついたてで台の上を隠すことができます.ついたてで隠したあと,ついたての後ろの台の上に人形を1体追加します.もちろん,人形を追加している様子は,乳児から見えるようにします.そして台の裏に隠れている人が,こっそり人形を1体だけ台の上から持ち去ります.
被験者の乳児の目線だと,ひとつ目の実験と同じく,ついたてで隠される前に1体の人形があり,ついたてで隠された状態でもう1体追加されたことが分かっています.
ここでついたてを取り除きます.台の上には人形が1体しかありません.この結果に対して,乳児は台の上をじっと凝視します.これは,予想外の結果が起きたため,興味を惹かれ,対象を見つめているのだと考えられます.

さてここで重要なのは,なぜ,2つの実験で乳児の反応が変わったのか,ということです.ひとつ目の実験の結果が予想通りであり,ふたつ目の実験の結果が予想に反したものだったから,と考えるのが自然でしょう.ということは,乳児は台の上の人形の数を予想できていた,1+1=2 であると,「分かって」いたということになります.
この他にも,乳幼児の数に関する実験は多数あります.乳児の頃から存在している計算能力を「生得算術(innate arithmetic)」といいます.数の概念の基礎は,人間が生まれながらに持っているのかもしれませんね.
詳しく知りたい方は,以下の書籍をご参照ください.
G.レイコフ, R.ヌーニェス 著 植野義明, 重光由加 訳『数学の認知科学』(平成24年)丸善出版.
余談ですが,サルなどの霊長類やアライグマ,ラット,ハトやカラスといった,頭の良い動物たちも小さな自然数を理解しています.一方で,奇跡のアホ「ダチョウ」などは数を全く理解できません.カラスとダチョウの知能の比較については,オールマイティ・ラボさんの動画が面白く短くまとまっているためオススメです(他のサイト(YouTube)に飛びます).
コラム:有理数,無理数は謎翻訳!?変な翻訳はよくあること
有理数は英語で「rational number」といいます.直訳すると「比で表せる数」となります.つまり,分数で表せる数のことです.
無理数は「irrational number」といい,直訳で「比で表せない数」となります.
有理数も無理数も,あまり良い翻訳ではありません.
良くない翻訳は他にもあります.
中学から聴いてきたであろう「方程式」という言葉は,中国の書籍から取ってきた言葉で,正直なところ「方程」ってナニ,と聞かれると困ります.書籍にあった言葉をそのまま持って来ちゃっただけですので.ちなみに「方程式」は英語で「equation」といいます.
大学に入ってからだと,「行列」と「行列式」を英語にしたとき,あまりに別物で驚くこともあるでしょう.
日本語には,「漢字」という立派な表意文字5意味を持った文字がありますが,数学では,漢字の意味は無視して,定義をしっかり押さえることが重要な場面があります.
こういった変な翻訳は,数学に限った話ではありません.近年話題になっているAIを支える分野である機械学習では,「feature」を「特徴量」と訳すことが流行っています.機械学習の「feature」には,必ずしも「量」と呼べないものも含まれるのですが,「特徴量」という呼び方を定着させたい様です.全く理屈が分かりません.
何が言いたいかと言いますと,翻訳された用語は,理に適った翻訳がなされているとは限らないため,字面だけ見て意味を断定することは止めた方がよいですよ,というお話でした.
コラム:ピタゴラス教団と無理数
むかしむかし6紀元前6世紀ごろ,古代ギリシャに数を崇めるピタゴラス教団という団体がありました.トップはあのピタゴラスです.ピタゴラスの定理(三平方の定理)などで有名な人物です.当時の古代ギリシャでは,自然現象や物質といった万物の根源(アルケー)7社会科科目「倫理」の重要ワードを考察することが流行していました.ピタゴラスの考えたアルケーは,もちろん「数」です.
「数を崇める」と言いましたが,ここでいう数とは「自然数」のことです.「調和の取れた世界は,自然数によって成り立っている.(正の)有理数も自然数の比で表すことができる」という信念のもとで教団は成り立っていました.「世界を見てみよ.和音を構成する音と音の関係から,惑星の運動まで,すべて数学でできている.数と数学こそが世界を作っているのだ!」
しかし,ピタゴラスと教団の幹部は,知っていました.決して自然数の比では表せない数が存在していることを.
無理数の存在に気付くのは簡単です.1辺1cmの正方形の対角線の長さを計算してみれば良いのです.ピタゴラスの定理を使って求めることもできますね.

こうして,無理数の存在は教団の信念を揺るがせ,教団の崩壊を招いたのでした.
ピタゴラス教団の崩壊を招いたのは無理数の存在.
最も身近な無理数を求める方法は,ピタゴラスの定理を使うこと.
なんとも因果な関係です.
このお話は
A. J. ハーン著『解析入門part1 アルキメデスからニュートンへ』(2001)シュプリンガー・フェアラーク東京.
の序盤の内容を参考に作られています.
コラム:世界は無理数で溢れている
みなさんは「無理数を具体的に挙げよ」と言われたとき,どのような数を挙げますか.円周率の \pi や \sqrt{n}8ただし n は平方数でない といった数を答えるのではないでしょうか.先の単元まで勉強している人であれば,ネイピア数 e や,n乗根を答えるかもしれません.
他にありませんか?
え?無い?
そんなことはありません.
名前のない無理数があたり一面にあるのです.
例えば,次のような無理数を考えてみましょう.整数部分は 0,小数点以下は 0 を1個,そのあと 1 をひとつ,0 を2個,1 をひとつ,0 を3個,1 をひとつ……と続けると,次のような数ができます.
0.01001000100001000001 \cdots \\
循環しない無限小数なので,無理数であることが分かるでしょう.
別の単元のコラムで語りますが,無理数は有理数よりもたくさんあります.名前のない無理数がたくさんあるのです.
世界は無理数で溢れています.
ちなみに例で挙げた数は,数式で表すことができます.
0.01001000100001000001 \cdots \\
は次のように表せます.
\sum_{n=1}^{\infty} \left( \frac{1}{10} \right)^\frac{n(n+3)}{2} \\ 数式も名前と捉えるならば,この無理数に名前はあったのです9 \sumとはなんぞや?という人は「総和」という言葉を調べてみてください.もしくは,こちらのページか,のちに作成する予定のページをご参照ください..
循環小数の分数への変換
前の節で,有理数は全て分数で表せると言いました.ということはもちろん,有理数である循環小数を分数で表すことができます.ここでは,循環小数を分数へ変換する方法について解説します.
循環小数を分数へ変換するときの発想は,循環部分が消えるように工夫して計算をすることです.
0.\dot{3} = 0.3333333 \cdots \cdots を分数に変換してみましょう.
まず, x = 0.\dot{3} とおきます.さらに 10x について考えると, 10x = 3.\dot{3} = 3.3333333 \cdots \cdots となります.ここで, 10x - x をすると,循環部分が打ち消しあい, 9x = 3 が残ります.
問題の解答として書くならば,以下のようになります.
解答例.
x = 0. \dot{3} = 0 .3333 \cdots とおく.
また, 10x = 3. \dot{3} = 3 .3333 \cdots となる.
10x から x を引いて,
\begin{aligned}
10x - x &= 3. \dot{3} - 0. \dot{3} \\
9x &= 3 \\
x &= \frac{1}{3}
\end{aligned}
よって,
\begin{aligned} 0. \dot{3} = \frac{1}{3} \end{aligned}
ちなみに,循環部分を消す操作を分かりやすく書くと,以下のようになります.
補足.
\begin{aligned}
10 &x&= 3 &.3333 \cdots \\
- \large{)} &x&= 0 &.3333 \cdots \\
\hline
9 &x &= 3 & \\
&x &= \frac{1}{3} &
\end{aligned}
次に, 0.\dot{0}7692\dot{3} を分数に変換してみましょう.
まずは,x = 0.\dot{0}7692\dot{3} とおきます. 0.\dot{0}7692\dot{3} は6桁ごとに循環しているので, x を 10^6 倍,つまり 1000000 倍した,1000000 x から x を引けば循環部分が消えます.
解答例.
x = 0.\dot{0}7692\dot{3} とおく.
また, 1000000x = 76923. \dot{0}7692\dot{3} である.
1000000x から x を引いて,
\begin{aligned}
1000000x - x &= 76923. \dot{0}7692\dot{3} - 0.\dot{0}7692\dot{3} \\
999999x &= 76923 \\
x &= \frac{76923}{999999} \\
x &= \frac{8547}{111111} \\
x &= \frac{2849}{37037} \\
x &= \frac{77}{1001} \\
x &= \frac{1}{13} \\
\end{aligned}
よって,
\begin{aligned} 0.\dot{0}7692\dot{3} = \frac{1}{13} \end{aligned}
約分が大変でしたね.
この計算も循環部分の削除を分かりやすく書くと,以下のようになります.
補足.
\begin{aligned}
1000000 &x &= 76923&.076923 \cdots \cdots\\
- \large{)} &x &= 0&.076923 \cdots \cdots\\
\hline
999999&x &= 76923 & \\
&x &= \frac{76923}{999999} & \\
&x &= \frac{1}{13} &
\end{aligned}
それでは,いくつか例題を解いてみましょう.
例題2.
次の小数を分数に変換せよ.
(1) 0.125
(2) 0. \dot{1}
(3) 0. 1 \dot{6}
(4) 0. 4 \dot{0} \dot{3}
例題2の解答.
例題2の解答.
(1) 0.125
\begin{aligned}
0.125 &= \frac{125}{1000} \\
&= \frac{1}{8}
\end{aligned}
有限小数の問題も混ぜてみました.
(2) 0. \dot{1}
x = 0. \dot{1} とおく.
また, 10x = 1. \dot{1} となる.
10x から x を引いて,
\begin{aligned}
10x - x &= 1. \dot{1} - 0. \dot{1} \\
9x &= 1 \\
x &= \frac{1}{9}
\end{aligned}
よって,
\begin{aligned} 0. \dot{1} = \frac{1}{9} \end{aligned}
(補足)
\begin{aligned}
10 &x&= 1 &.1111 \cdots \cdots \\
- \large{)} &x&= 0 &.1111 \cdots \cdots \\
\hline
9 &x &= 1 & \\
&x &= \frac{1}{9} &
\end{aligned}
(3) 0. 1 \dot{6}
x = 0. 1 \dot{6} とおく.
また, 10x = 1. \dot{6} となる.
10x から x を引いて,
\begin{aligned}
10x - x &= 1. \dot{6} - 0. 1\dot{6} \\
9x &= 1.5 \\
90x &= 15 \\
x &= \frac{1}{6}
\end{aligned}
よって,
\begin{aligned} 0. 1 \dot{6} = \frac{1}{6} \end{aligned}
(補足)
\begin{aligned}
10 &x &= 1&.666666 \cdots \cdots \\
- \large{)} &x &= 0&.166666 \cdots \cdots \\
\hline
9&x &= 1.5 \\
&x &= \frac{15}{90} \\
& &= \frac{1}{6}
\end{aligned}
(4) 0. 4 \dot{0} \dot{3}
x = 0. 4 \dot{0} \dot{3} とおく.
また, 100x = 40 . 3 \dot{0} \dot{3} となる.
100x から x を引いて,
\begin{aligned}
100x - x &= 40. 3 \dot{0} \dot{3} - 0. 4 \dot{0} \dot{3} \\
99x &= 39.9 \\
x &= \frac{399}{990} \\
x &= \frac{133}{330}
\end{aligned}
よって,
\begin{aligned} 0. 4 \dot{0} \dot{3} = \frac{133}{330} \end{aligned}
(補足)
\begin{aligned}
100 &x &= 40&.30303 \cdots \cdots \\
- \large{)} &x &= 0&.40303 \cdots \cdots \\
\hline
99&x &= 39.9 \\
&x &= \frac{399}{990} \\
&x &= \frac{133}{330}
\end{aligned}
実数直線と絶対値
最後に,実数の絶対値のお話をします.
実数と直線上の点を1対1に対応させ,また数の大小関係が直線上の左右の位置関係10向きと位置関係と一致する直線を実数直線(もしくは数直線)と呼びます. 全ての実数に対して,対応する点が直線上に必ず1つ存在するということです.例えば,0.5 が対応する点が実数直線上に1つあり,他の異なる実数の点と重なることはありません.また 0 に対応する点のことを原点といい \mathrm{O} で表すことがあります.
ここでは変則的な実数直線は考えず,差が等しい2つの実数であれば,どのような2つの実数であっても,数直線上の対応する2点間の長さが変わらないものとします.例えば「1 と -1」の組と「-2 と -4」の組の差は同じなので,「1が対応する点 と -1 が対応する点の間の長さ」と「-4が対応する点 と -2 が対応する点の間の長さ」は等しくなります.
さらに,多くの場合,数直線の右側にいくほど大きな数になり,原点より左側の点に対応する数は負の数となります.
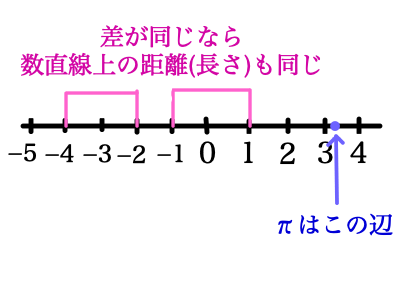
さて,ここでは実数直線上の2点間の長さのことを距離と呼ぶことにします.
原点 \mathrm{O}( 0 に対応する点のこと)から,実数 a に対応する点までの距離のことを,実数 a の絶対値といい, |a| と書きます.
絶対値の定義を正確に書くと以下のようになります.
実数 a の絶対値.
\begin{cases}
|a| = a (a \geqq 0 のとき) \\
|a| = -a (a < 0 のとき)
\end{cases}
いくつか例を挙げてみましょう.
\begin{array}
||2| &= 2 \\
|-4| &= 4 \\
|0| &= 0 \\
|-0.5| &= 0.5
\end{array} ここまでの例を見て,
「なんだ!マイナス記号を外すだけか!」なんて勘違いをしてはいけません!
次の例を見てみましょう.
|x+2|を求めよ.(ただし,x < -3 とする) \\ |x + 2| = -x - 2 \\ \\ \\ 実数 a に対して |a - 2| を求めよ.\\ a \geqq 2のとき\\ |a - 2| = a - 2 \\ a < 2のとき\\ |a - 2| = -a + 2
上記の 「 |x + 2 | を求めよ」の場合,x<-3 であることから, x + 2 は必ず負の数となります.よって,絶対値の定義より, a < 0 のとき, |a| = -a なので, |x + 2 | = - (x + 2) = - x - 2 となります.
上記の「実数 a に対して |a-2| を求めよ.」も同様です.絶対値の定義に当てはめて, a - 2 \geqq 0 のときと, a - 2 < 0 のときに場合分けして考えています.
それでは,例題を解いてみましょう!
例題3.
次の値を求めよ.ただし, a は任意の実数, y については y < - 2 であるとする.
(1) |2|
(2) |0|
(3) |-3|
(4) |a - 1|
(5) |y + 1|
例題3の解答.
解説.
絶対値を求めるときのポイントは,定義に忠実になることです!
(再掲)実数 a の絶対値.
\begin{cases}
|a| = a (a \geqq 0 のとき) \\
|a| = -a (a < 0 のとき)
\end{cases}
解答.
(1) |2| = 2
(2) |0| = 0
(3) |-3|= 3
(4) |a - 1|
(補足)
a - 1 \geqq 0 の場合と, a - 1 < 0 の場合で,場合分けをして考える.
(解答)
a \geqq 1 のとき
|a - 1| = a - 1
a < 1 のとき
|a - 1| = - (a - 1) = - a + 1
(5) |y + 1|
y < - 2 より, y + 1 は必ず負になるので,
|y + 1| = - (y + 1) = - y - 1
コラム:さまざまな距離 「距離?今,距離って言いました?」
高校数学には出て来ませんが,実は距離には色々あるため,単に距離と言われても,文脈や状況によっては「何のこと?距離の名前は?定義は?もしくは両方言って」となることがあります.気になる人は「マンハッタン距離(Wikipediaのページ)」や「レーベンシュタイン距離(Levenshtein distance)」などで調べてみてください.
ユークリッド空間上にも無数に距離がありますし,文字列間の距離11色々あるよ,木構造の距離12色々あるよ,何でもあります.それでは,何でも距離と呼んでいいのかというと,そんなこともなく,距離の公理を満たす必要があります.詳しくは,この記事やWikipediaの距離の定義の項目を読んでください.もちろん興味がある人だけでOKです.
また,距離と名の付くものでも距離でない場合もあります13統計や機械学習に出てくる,カルバック・ライブラー情報量のことをカルバック・ライブラー距離と呼ぶことがありますが,対称性はありませんし,三角不等式も満たさないので,どこに距離の要素があるのか謎です.むしろ距離の要素が無い..もう訳が分からないよ.
コラム:実数の定義と連続性[難・読み飛ばし推奨]
実は高校数学では,有理数・無理数・実数の定義がキチンとされていません.曖昧な部分が残っています.たいていの教科書や参考者はそれを「どーでもいい」と考えていますし,キチンと考えている参考書は「上手く誤魔化して」います.この記事の定義も曖昧さを誤魔化しています.
それでは厳密に書けば良いかというと,その場合,難しくなり過ぎてしまい,脱落者が出てしまいかねません.
高校数学は,この単元に限らず,定義や定理を曖昧にすることがあります.定理を曖昧にしている例は簡単に挙げられます.展開公式に (a + b)^2 = a^2 + 2ab + b^2 がありますが,この公式は ab = ba と言う法則を自然と使っています.大学以降で習う数学の対象には,この性質が成り立たないものがあります.この公式は,実数や複素数を中心に扱う高校数学だから成り立つのです.つまり,公式の前提条件に「抜け」があるのです.
しかし,こういったことを細かく確認していては先に進めませんし,何より高校で学習する範囲や難易度を超えてしまいます.そのため高校数学では,この先の単元も含めて,様々な部分が曖昧にされているのです.厳密にする必要がないとも言えます.
高校数学と大学の数学(特に理学部の数学)は別モノだと感じる人も多いようですが,原因はここにあります.理学部の数学では,基本に立ち返り,曖昧な部分を無くしながら,曖昧さのない定義の解説と定理の証明を繰り返します.高校数学は大学受験のために「素早く計算する」ことに力を入れやすいですが,大学数学では「納得できるまで考える」ことが重要となります.演習の量や質も大きく変わります.
さて話が脱線してしまいました.実数の定義の話に戻りましょう.
実数の定義については,厳密でなくても良いのですが,数学Ⅲでは少し困ったことになります.数学Ⅲでは,(実)関数の連続性について触れます.連続性については,隙間なく繋がっているイメージを持てば十分でしょう.実はこの連続性,関数の定義域や値域が実数であることから,間接的に実数の連続性に触れているのです14(というか実数の連続性と同値の定理が登場しますし,中間値の定理とか.実数列の極限の収束といい,実質的に実数の連続性について話しているのでは?).有理数全体の集合は隙間がないように見えます.しかし,有理数の集合を x^2 \leqq 2 で区切ると最大値が有理数の範囲にありません.有理数全体の集合は,隙間だらけなのです.
実関数の連続性をきちんと説明しようとすると,有理数の隙間や「実数の連続性」を説明せねばなりません.しかし現状は,実関数の連続性は登場させるが,実数の連続性は曖昧にしています.
厳密に議論するためには,実数をしっかりと定義する必要があります.つまり,実数を厳密に構成する(実数を作る)必要があります.主な実数の作り方は3つあります.興味のある方は調べてみてください.
- 公理を使って実数を作る
- デデキントの方法で作る
- カントールの方法で作る
次のコラムでは,実数の公理を少しだけ紹介したいと思います.そして厳密に議論されたものだけで証明を行う難しさを,少しだけ体験できるようにしてみました.興味があればそちらのコラムもご覧ください.
コラム:挑戦!実数の公理から当たり前の命題を証明しよう!
高校数学では「実数」の定義が曖昧に誤魔化されています.
ここでは「実数」の構成の仕方のひとつ,公理を与える方法をざっくりと説明します.
その後,厳密に示されたわずかな条件から,私たちが当たり前に使っている定理を証明する体験をしてみましょう.前のコラムと合わせて,高校数学と大学(理学部)でやる数学のギャップを少しでも埋めようじゃないか,という試みです.
このコラムは,以下の書籍の内容を参考にしています.
杉浦光夫 著『解析入門Ⅰ』(1980)東京大学出版会.
この本は,最初に実数の持つ17の性質を示し,その17の性質を同時に満たす集合が実数全体の集合のみであることを示すことから始まります.その17の性質を纏めてざっくり言うと,連続な順序体です15気になる人は,調べるか,前述の本を買ってみましょう!.
ここでは17の性質のうち,最初の10の性質,実数は体(たい)であるという部分を紹介し,少し意外な証明問題に挑戦します.実はこのコラム,ほとんどタイトル詐欺で「体の定義から当たり前の命題を証明しよう」が正しい内容です.
それでは性質を10個紹介します.
体は集合 \mathbb{R} の任意の要素 a,b に対して,和 a+b と積 ab が定義され,次の10の条件を満たす.
- (ルール1) a + b = b + a
- (ルール2) (a + b) + c = a + (b + c)
- (ルール3) \mathbb{R} の要素 0 が存在し,全ての \mathbb{R} の要素 a に対して,a + 0 = a を満たす.
- (ルール4)任意の \mathbb{R} の要素 a に対して,a + (-a) = 0 を満たす \mathbb{R} の要素 -a が存在する.
- (ルール5)ab = ba
- (ルール6)(ab)c = a(bc)
- (ルール7)a(b + c) = ab + ac ,(a + b)c = ac + bc
- (ルール8)\mathbb{R} の要素 1 が存在し,全ての \mathbb{R} の要素 a に対して,a1 = a を満たす.
- (ルール9)0 でない任意の \mathbb{R} の要素 a に対して,a a^{-1} = 1 を満たす \mathbb{R} の要素 a^{-1} が存在する.
- (ルール10)1 \neq 0
それでは,今から皆さんには,この10個のルール以外の,全ての数学知識を忘れてもらいます!
問題.
上記の(ルール1)から(ルール10)までの10個のルールのみを使い,以下の命題,及び,等式を証明してください.
(1) (ルール3)を満たす 0 は \mathbb{R} において唯一つのみ存在する.( ヒント:問題の言い換え「(ルール3)の性質を満たす要素は,\mathbb{R} において複数存在しない」)
(2) - (- a) = a
(3) 0a = 0
(4) (-1)(-1) = 1
まとめ
本記事では,実数,無理数,有理数について解説しました.また,絶対値についても学習しました.
今回の内容は,計算が少なく文字が多いため,手こずった人もいるかもしれません.最後に,今後の学習のためにも,これだけは覚えてほしいという部分を再掲して終わりたいと思います.
ちなみに次回の記事では,無理数の続き,平方根について学習します.
今回の内容の重要な部分
・循環しない無限小数のことを無理数という
・無理数でない実数は有理数
・有理数でない実数は無理数
・循環小数を分数に変換する方法
・(再々掲)実数 a の絶対値の定義.
\begin{cases}
|a| = a (a \geqq 0 のとき) \\
|a| = -a (a < 0 のとき)
\end{cases}
《PR》
関連ページ
演習問題
次のページ
(作成中)
前のページ