方べきの定理の練習問題

本記事には，方べきの定理を使って解ける基本的な問題と解答例があります．
方べきの定理をしっかりと使いこなせるようになりましょう．

方べきの定理が分からない人は以下の記事をご参照ください．

円と直線の定理

　　　

問題1

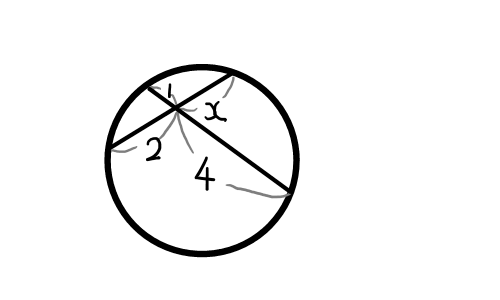
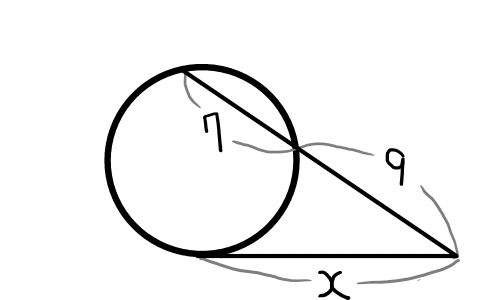
以下の図の $x$ の値を求めよ．

　

（1）

　　　

（2）

　　　　

（3）

　　　　　　

（4）

　　　　　　　　

（5）

問題2

ある円に2本の弧 $\mathrm{AB}$ と弧 $\mathrm{CD}$ がある．この2本の弧が円の内側の点 $\mathrm{E}$ で交わり，$\mathrm{AB} = 18$ ，$\mathrm{AE} = 6$ ，$\mathrm{CE} = 8$ であるとき，線分 $\mathrm{DE}$ の長さを求めよ．

問題1の解答例

方べきの定理について簡単に復習しておきます．

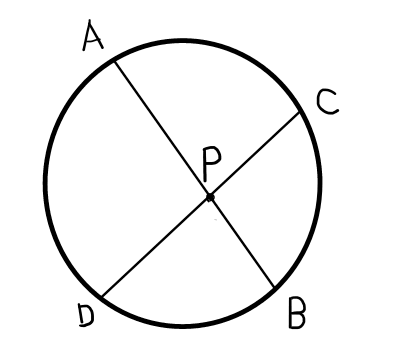
方べきの定理．
2本の弧 $\mathrm{AB}$ と弧 $\mathrm{CD}$ の交点を $\mathrm{P}$ とするとき，以下の式が成り立つ．
$\mathrm{AP} \cdot \mathrm{BP} = \mathrm{CP} \cdot \mathrm{DP}$

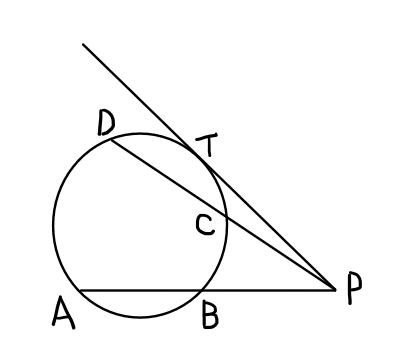
また，上の図のように円の接線と弧 $\mathrm{AB}$ の交点を $\mathrm{P}$，接点を$\mathrm{T}$ とするとき以下の式が成り立つ．
$\mathrm{AP} \cdot \mathrm{BP} = \mathrm{PT}^2$

　　　　

それでは，解答例に移りたいと思います．

　　　

　　　　

（1）

解答例．
方べきの定理より
$\begin{aligned} 2 \cdot x &= 1 \cdot 4 \\ 2x &= 4 \\ x &= 2 \end{aligned}$

　　

　　　

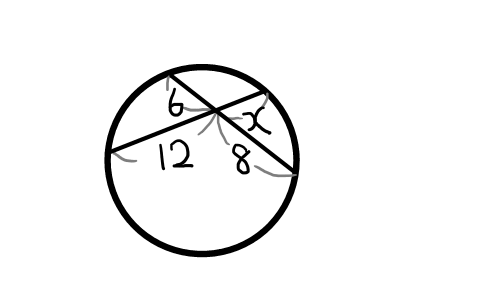
（2）

解答例．
方べきの定理より
$\begin{aligned} 12 \cdot x &= 6 \cdot 8 \\ 12 x &= 48 \\ x &= 4 \end{aligned}$

　　　　

　　　　

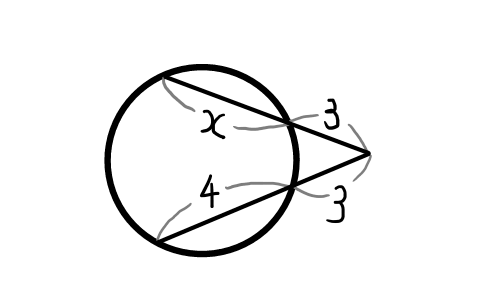
（3）

解答例．
方べきの定理より
$\begin{aligned} 3 ( x + 3) &= 3 (3 + 4) \\ 3 x + 9 &= 21 \\ 3 x &= 12 \\ x &= 4 \end{aligned}$

　　　　

　　　　

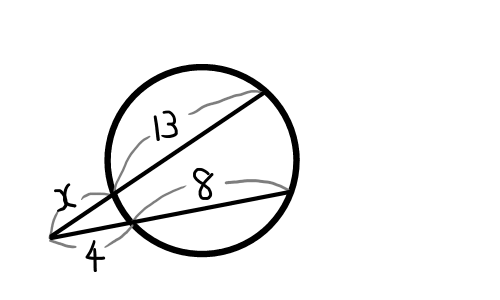
（4）

解答例．
方べきの定理より
$\begin{aligned} x ( x + 13) &= 4 ( 4 + 8 ) \\ x^2 +13x &= 48 \\ x^2 +13 x - 48 &= 0 \\ ( x - 3 )( x + 16 ) &= 0 \end{aligned}$
$x > 0$ より
$x = 3$

　　　

　　　　

（5）

解答例．
方べきの定理より
$\begin{aligned} x^2 &= 9 (9 + 7) \\ x^2 &= 3^2 \cdot 4^2 \\ \end{aligned}$
$x > 0$ より
$x = 12$

問題2の解答例

方べきの定理が使える図形の問題を，文章に変換しただけの問題です．

解答例．
$\begin{aligned} \mathrm{BE} &= \mathrm{AB} - \mathrm{AE} \\ &= 18 - 6 \\ &= 12 \end{aligned}$
方べきの定理より
$\begin{aligned} \mathrm{CE} \cdot \mathrm{DE} &= \mathrm{AE} \cdot \mathrm{BE} \\ 8 \cdot \mathrm{DE} &= 6 \cdot 12 \\ 8 \mathrm{DE} &= 72 \\ \mathrm{DE} &= 9 \\ \end{aligned}$

　　　　

「勝手気ままに高校数学」シリーズ一覧へ