絶対値を含む1次関数のグラフを描いてみる

本記事では絶対値を含む1次関数のグラフを描きたいと思います．お絵かきです．

遊びがメインですが，真面目な恩恵もあります．関数の問題では，グラフを描くことで問題の見通しが良くなる場合があります．絶対値を含む関数でもそれは同様です．
絶対値を含む関数のグラフを描く機会は少ないので，興味がある方は一緒に描いてみて下さい．

$y = |x|$

初めに $y = |x|$ のグラフを描いてみます．
グラフを描くときは，方程式や不等式の場合と同様に，絶対値の中が正の場合と負の場合に場合分けをして考えます．条件によって関数が変わるのです．

$y = |x|$ を場合分けすると，

(ⅰ) $x \geqq 0$ のとき，
　$y = x$
(ⅱ) $x < 0$ のとき，
　$y = - x$

グラフは以下のようになります．

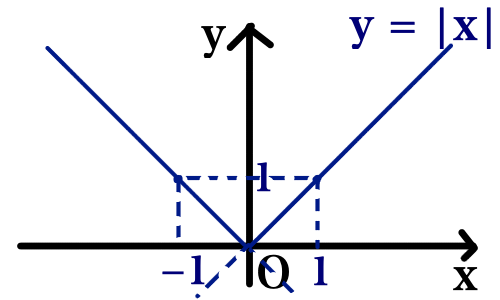
ちなみに，この関数のグラフを，場合分けを使わずに描くことができます．

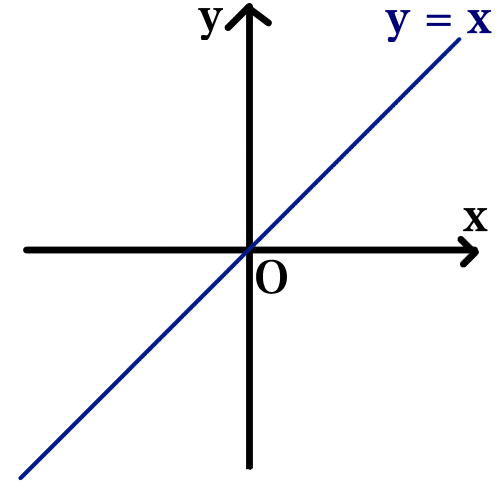
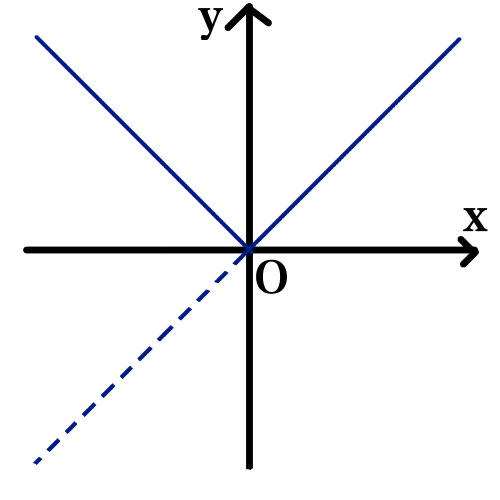
$y = x$ のグラフを描き，$y$ がマイナスになる部分を，$x$ 軸で折り返して¹$x$ 軸に関して対称移動させて形と描くこともできます．

基本的な形式　$y = |x - a|$

$y = |x - a|$ のグラフは $y = |x|$ を $x$ 軸方向に $a$ だけ平行移動させたグラフになります．

具体例を見てみます．

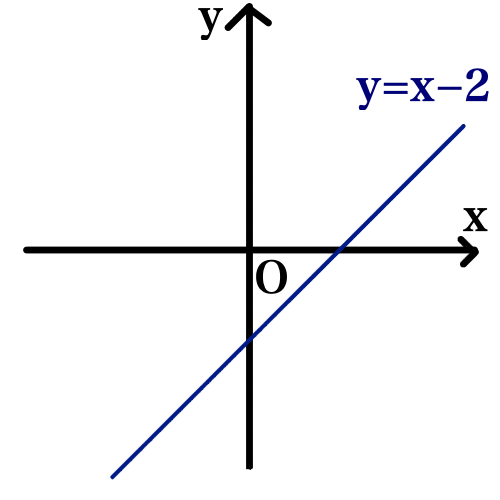
$y = |x - 2|$ のグラフを描くために場合分けをすると，

(ⅰ) $x \geqq 2$ のとき，
　$y = x - 2$
(ⅱ) $x < 2$ のとき，
　$y = - x + 2$

となります．グラフにすると以下のようになります．

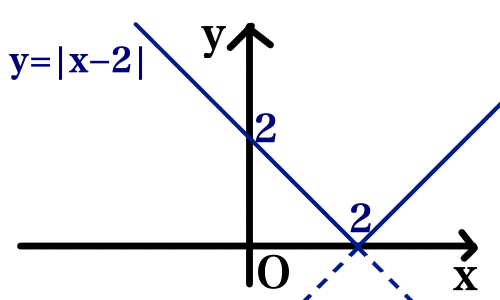
もちろん $y = x - 2$ のグラフを $x$ 軸で折り返したグラフと捉えることもできます．

絶対値記号の中に絶対値記号がある場合

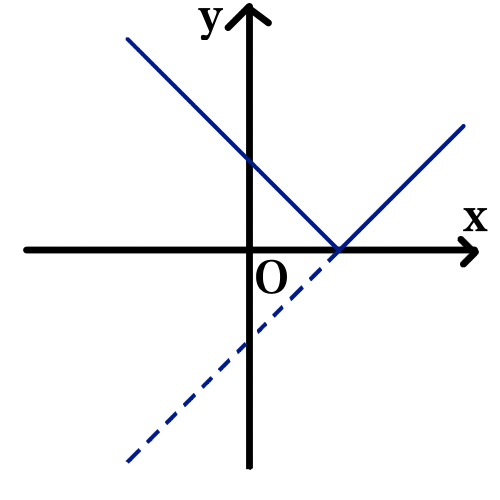
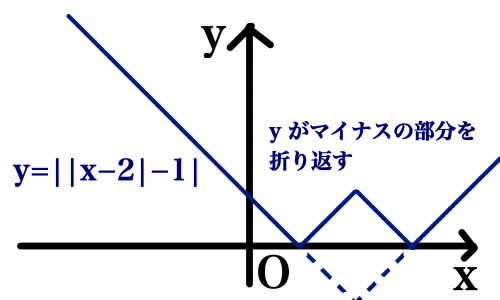
絶対値の中に絶対値のある関数のグラフを描きます．グラフを描く関数は $y = | |x - 2| - 1 |$ です．

まずは場合分けをして，範囲ごとにどのような関数になるか調べてみましょう．場合分けは内側の絶対値から行います．

(Ⅰ) $x \geqq 2$ のとき，
　 $y = | x - 2 - 1 | = |x - 3|$
(ⅰ) $x \geqq 3$ のとき，
　 $y = x - 3$
(ⅱ) $x < 3$ のとき，つまり $2 \leqq x < 3$ のとき，
　 $y = - x + 3$

(Ⅱ) $x < 2$ のとき，
　$y = | -( x - 2 ) - 1 | = | - x + 1 |$
(ⅰ) $x \leqq 1$ のとき，
　 $y = - x + 1$
(ⅱ) $x > 1$ のとき，つまり $1 < x < 2$ のとき，
　 $y = x - 1$

$y = | |x - 2| - 1 |$ のグラフは以下のようになります．

青い実線がグラフです．数字は面倒なので省略しました．

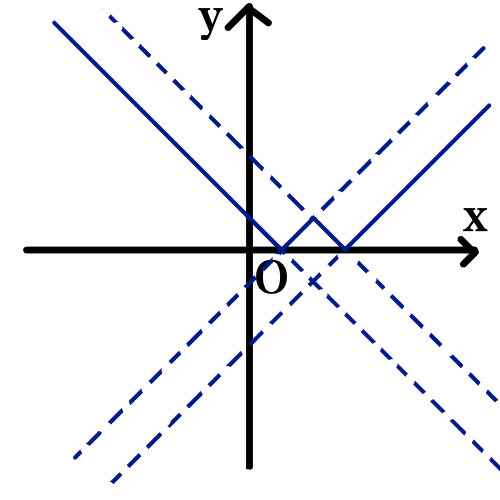
実は場合分けせずに描く方法もあります．

まずは $y = |x - 2|$ のグラフを描きます．

$y = |x - 2|$ のグラフを $y$ 軸方向に $-1$ 平行移動させます．

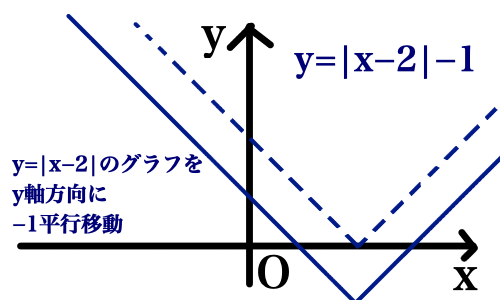
あとは $y$ がマイナスになる部分について， $x$ 軸で折り返せば完成です．

複数の絶対値記号がある場合

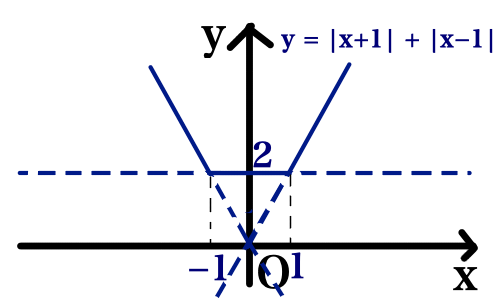
絶対値記号が複数ある関数のグラフを描きます．グラフを描く関数は $y = |x + 1| + |x - 1|$ です．

初めに $y = |x + 1| + |x - 1|$ のグラフを描くために場合分けをします．場合分けは次の3通りです．

• $x + 1$ と $x - 1$ が両方とも負である
• $x + 1$ が正， $x - 1$ が負である
• $x + 1$ と $x - 1$ が両方とも正である

さっそく場合分けしてみましょう．

(ⅰ) $x < - 1$ のとき，
　$y = - 2x$
(ⅱ) $-1 \leqq x < 1$ のとき，
　$y = 2$
(ⅲ) $x \geqq 1$ のとき，
　$y = 2x$

$y = |x + 1| + |x - 1|$ のグラフを描くと下の図のようになります．

絶対値を含む1次関数でお絵描きをしよう！

さらに絶対値記号を組み合わせることで，様々な形のグラフが描けそうです．

しかし，場合分けを細々と行うのは面倒なので，プログラムの力を借りることにしましょう！

pythonと２つのライブラリnumpyとmatplotlibを使用します．コードはjupyter notebook上で実行します．

とりあえず，$y = | | x - 8 | - 2 | + | x |$ のグラフを描いてみます．
コードは以下の通りです．

import numpy as np
import matplotlib.pyplot as plt

# -5から15まで0.1刻みの配列を作成
x = np.arange(-5, 15, 0.1)
y = abs(abs(x - 8) - 2) + abs(x)
plt.plot(x,y)
plt.show()

$y = | | x - 8 | - 2 | + | x |$ のグラフは以下のように出力されます．

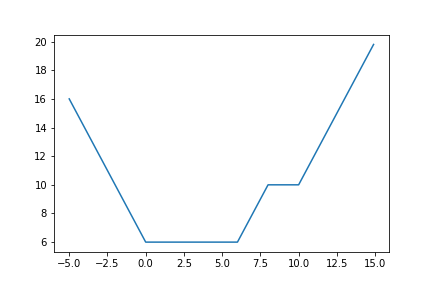
軸の設定は面倒なので，デフォルトに任せています．軸の数値に注意してください．

肝心のグラフはというと，なんというか普通ですね．

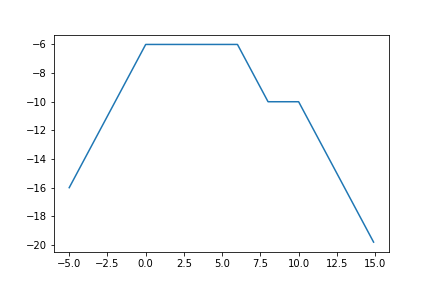
せっかくなのでプリン型にしてみます．おそらく関数全体にマイナスを掛ければ良いでしょう．
$y = - | | x - 8 | - 2 | - | x |$ を描いてみます．

# モジュールのインポートは省略
x = np.arange(-5, 15, 0.1)
y = - abs(abs(x - 8) - 2) - abs(x)
plt.plot(x,y)
plt.show()

出力．

次はせっかくなので，人間が描くにはメンドー過ぎる関数にします．

x = np.arange(-10, 10, 0.1)
y = abs(abs(abs(x - 4) - 2) - 1) + abs(x)
plt.plot(x,y)
plt.show()

出力．

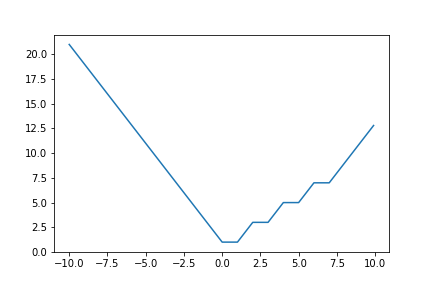
うーむ．ひっくり返して山型にしたいですね．

というわけで，$y = - | | | x - 4 | - 2 | - 1 | - | x |$

x = np.arange(-10, 10, 0.1)
y = - abs(abs(abs(x - 4) - 2) - 1) - abs(x)
plt.plot(x,y)
plt.show()

出力．

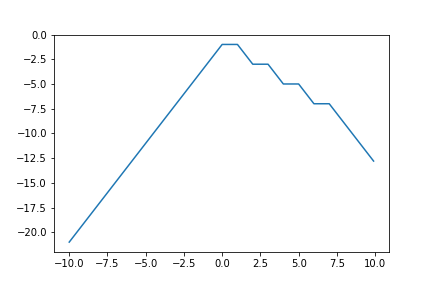
最後はもっとおかしな形にしてみます．

x = np.arange(-10, 10, 0.1)
y = abs(abs(abs(2 * x - 5) - 2) - 1) + abs(-3 * x) - abs(4 * x + 1) + x
plt.plot(x,y)
plt.show()

出力

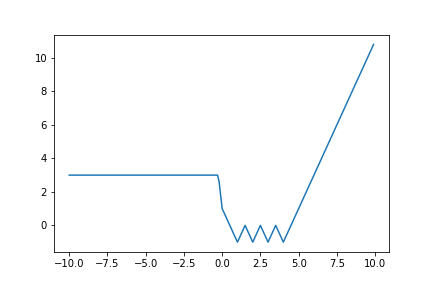
おしまい．