複素数平面の基礎1
本記事では,複素数平面(複素平面,ガウス平面)の基本的な内容について解説します.
前提として,数学Ⅱで学習する程度の複素数の性質は知っているものとします.
自信がない方は,以下の記事をご参照ください.
複素数平面について
複素数zは,実数x, yを用いてz = x + y i と表されます.
そこで複素数を実数 x, y の組と考え,複素数z = x + y i と平面座標上の点( x , y )を1対1で対応させます.例えば,z = 2 + i の場合,平面上の座標( 2 , 1 )となる点と対応させます.平面ベクトル( 2 , 1 )と対応させていると考えても良いでしょう.
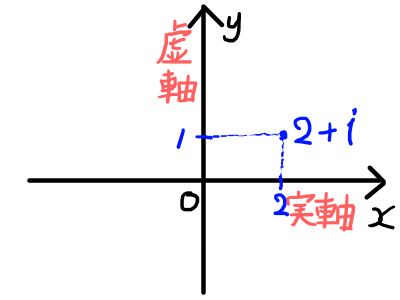
このように,複素数と点を1対1に対応させた平面のことを複素数平面といいます.また,ガウスの研究業績が大きいことからガウス平面と呼ばれることもあります1ガウス以前にも複素数を幾何的に考えた人はいますが,現在のような形に体系化したのはガウスが初めてであるため,ガウスの名前が用いられています..
実部の値に対応している軸(今回の場合はx軸)を実軸といい,虚部の値に対応している軸(今回の場合はy軸)を虚軸といいます.
虚部,実部を表す記号と複素数の絶対値
z = x + yi に関して, x を z の実部といい \mathrm{Re} (z) と表します.一方, y を z の虚部といい \mathrm{Im} (z) と表します.
また,複素数の絶対値は以下のように定義されます.
定義(複素数の絶対値).
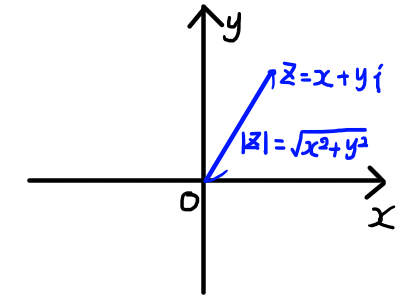
複素数平面上の点 z = x + yi から原点 \mathrm{O} までの距離 \sqrt{x^2 + y^2} を z の絶対値とよび, |z| と表します.
基本的な定理
定理1.
z + \overline{z} = 2 \, \mathrm{Re} (z)
証明1.
z = a +biとおく.
\begin{aligned}
z + \overline{z} &= (a +bi) + (a - bi)\\
&= 2a \\
&= 2 \, \mathrm{Re} (z)
\end{aligned}
定理2.
z - \overline{z} = 2i \, \mathrm{Im} (z)
証明2.
z = a +biとおく.
\begin{aligned}
z + \overline{z} &= (a +bi) - (a - bi)\\
&= 2bi \\
&= 2i \, \mathrm{Im} (z)
\end{aligned}
定理3.
z \overline{z} = |z|^2
証明3.
z = a +biとおく.
\begin{aligned}
z \overline{z} &= (a +bi)(a - bi)\\
&= a^2 +b^2 \\
&= (\sqrt{a^2 +b^2})^2 \\
&= |z|^2
\end{aligned}
定理4.
\overline{z^n} = \overline{z}^n
証明4.
zを複素数とする.
2つ以上の複素数 \alpha,\beta, \gammaに関して\overline{\alpha} \overline{\beta} \overline{\gamma} = \overline{\alpha \beta \gamma}であることを利用すると,
\overline{z^n} = \overline{z}^n
複素数の極形式
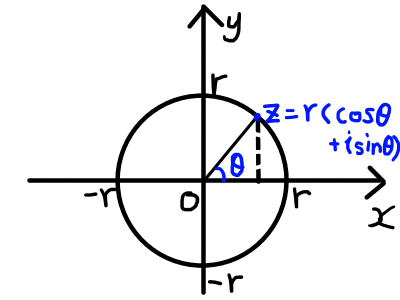
複素数平面上で,複素数 z を表す点を\mathrm{P}とします.実軸の正の側を始線として,動径\mathrm{OP}について回転角\thetaを考えます.
ここで原点\mathrm{O}を中心とする半径 r = |z| の円に関して,複素数を以下のように三角関数を用いた形で表せます.
z = r(\cos{\theta} + i \sin{\theta})このような形式の複素数の表し方を,複素数の極形式といいます.
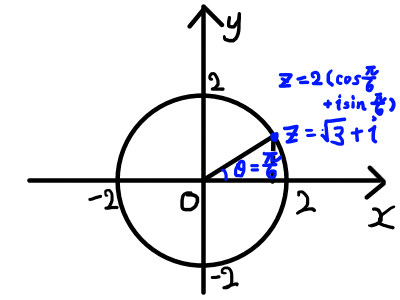
例として,z = \sqrt{3} + i を極形式で表してみましょう.
\begin{aligned}
|z| &= \sqrt{\left( \sqrt{3} \right)^2 +1^2}\\
&= \sqrt{3 +1} \\
&= 2
\end{aligned}
よって,
\begin{aligned}
z &= \sqrt{3} + i\\
&= 2 \left( \frac{\sqrt{3}}{2} + \frac{1}{2} \, i \right) \\
&= 2 \left( \cos{\frac{\pi}{6}} + i \, \sin{\frac{\pi}{6}} \right) \\
\end{aligned}
次回の記事
次回の記事では,複素数の加減乗除の計算が,複素平面上でどのように表されるかについて解説します.
今までの複素数は,せいぜい方程式の解で必要だっただけの概念ですが,複素平面上での振る舞いを知ると一気に面白くなります!
↓続きの記事↓

