複素数平面の基礎2 〜加減乗除と複素数平面〜
本記事では,複素数の加減乗除が複素数平面上でどのように表されるかを解説したいと思います.
複素数や複素数平面の基礎的な知識は既知であるとします.
自信がない方は,以下の記事をご参照ください.
複素数の加法と複素数平面
複素数の加法が,複素数平面上でどのような振る舞いをするか見てみましょう.
2つの複素数を z_1 = x_1 + y_1 i,z_2 = x_2 + y_2 i とします.
その和は,
\begin{aligned}
z_1 + z_2 &= x_1 + y_1 i + x_2 + y_2 i \\
& = (x_1 + x_2 ) + (y_1 + y_2 ) i \\
\end{aligned}
となります.
それぞれの複素数を複素平面上の座標で見ると,
z_1 : ( x_1 , y_1)
z_2 : ( x_2 , y_2)
z_1 + z_2 : (x_1 + x_2 , \, y_1 + y_2 )
複素数の和の座標は,座標の各成分の値を足したものになっています.
これはベクトルの和と同じです.
つまり複素数の和は,複素数平面上の図で表すと,ベクトルと同様に以下のようになります.
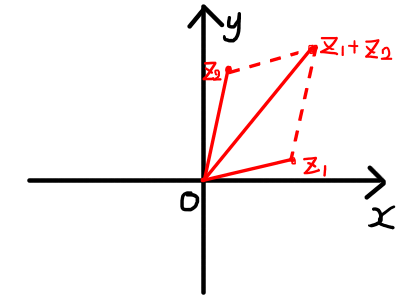
複素数の減法と複素数平面
次に複素数の減法が,複素数平面上でどのように表されるかを見てみましょう.
2つの複素数を z_1 = x_1 + y_1 i,z_2 = x_2 + y_2 i とします.
その2つの複素数の差は,
\begin{aligned}
z_1 - z_2 &= x_1 + y_1 i - ( x_2 + y_2 i ) \\
& = (x_1 - x_2 ) + (y_1 - y_2 ) i \\
\end{aligned}
となります.
それぞれの複素数を複素平面上の座標で見ると,
z_1 : ( x_1 , y_1)
z_2 : ( x_2 , y_2)
z_1 - z_2 : (x_1 - x_2 , \, y_1 - y_2 )
複素数の差の座標は,座標の各成分の値を引いたものとなっています.
加算の場合と同様に,ベクトルの差と同様の形となります.
複素数平面上で表すと以下のようになります.
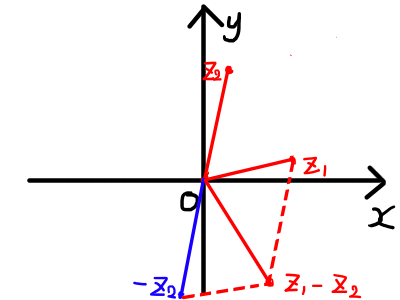
複素数の乗法と複素数平面
次に複素数の乗法について,複素数平面上で見てみましょう.
今回は複素数を極形式で表します.
2つの複素数を z_1 = r_1 (\cos{\alpha} + i \, \sin{\alpha}),z_2 = r_2 (\cos{\beta} + i \, \sin{\beta}) とします.
その2つの複素数の積を計算してみましょう.
\begin{aligned}
z_1 z_2 &= r_1 r_2 (\cos{\alpha} + i \, \sin{\alpha}) (\cos{\beta} + i \, \sin{\beta}) \\
& = r_1 r_2 (\cos{\alpha}\cos{\beta} + i \, \sin{\alpha}\cos{\beta} + i \, \sin{\beta}\cos{\alpha} - \sin{\alpha}\sin{\beta} ) \\
&= r_1 r_2 \{ (\cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta} ) + i \, (\sin{\alpha}\cos{\beta} + \sin{\beta}\cos{\alpha}) \} \\
&= r_1 r_2 \{ \cos{( \alpha + \beta ) } + i \, \sin{(\alpha + \beta)} \} \\
\end{aligned}
となります.
複素数 z の極表示における回転角 \theta を \arg{z}と表すとすると, | z_1 z_2 | = r_1 r_2 , \arg{ ( z_1 z_2 ) } = \arg{ z_1} + \arg{z_2} であることが分かりました.
複素数 z_1 に z_2 を掛けると,z_1 の点を \beta だけ回転させて,絶対値に r_2 掛けた点に移動します1面白いですね.
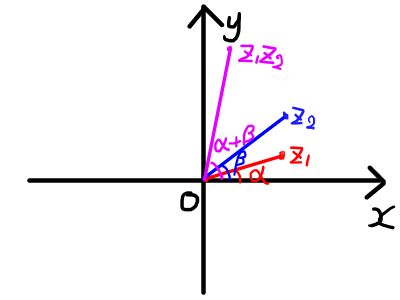
複素数の除法と複素数平面
最後に除法について考えてみましょう.
今回も複素数を極形式で表します.
2つの複素数を z_1 = r_1 (\cos{\alpha} + i \, \sin{\alpha}),z_2 = r_2 (\cos{\beta} + i \, \sin{\beta}) とします.
その2つの複素数の割り算を計算してみましょう.
\begin{aligned}
\frac{z_1}{z_2} &= \frac{r_1 (\cos{\alpha} + i \, \sin{\alpha})}{r_2 (\cos{\beta} + i \, \sin{\beta})} \\
&= \frac{r_1}{r_2} \cdot \frac{(\cos{\alpha} + i \, \sin{\alpha})}{(\cos{\beta} + i \, \sin{\beta})} \cdot \frac{(\cos{\beta} - i \, \sin{\beta})}{(\cos{\beta} - i \, \sin{\beta})} \\
&= \frac{r_1}{r_2} \cdot \frac{(\cos{\alpha} + i \, \sin{\alpha}) \{ \cos{(-\beta)} + i \, \sin{(- \beta)}) \} }{\cos^2{\beta} + \sin^2 {\beta}} \\
&= \frac{r_1}{r_2} \cdot \cos{(\alpha - \beta)} + i \, \sin{(\alpha - \beta)} \\
\end{aligned}
となります.
よって, \left| \frac{z_1}{z_2} \right| = \frac{r_1}{r_2} , \arg{ \left( \frac{z_1}{z_2} \right) } = \arg{ z_1} - \arg{z_2} であることが分かりました.

