配列の編集距離(ハミング距離,レーベンシュタイン距離)
距離の公理を満たすものは何でも距離と呼べます.
つまり配列(文字列)同士を考えることも可能なのです.
ちなみに距離の公理は以下の通りです.
距離の公理.
集合Xの任意の要素 a,b,c に関して,2変数関数 d が以下の条件を満たすとき,d のことを距離,または距離関数という.
d(a, b) = 0 \Leftrightarrow a = b
d(a, b) = d(b, a)
d(a, b) + d(b, c) \geqq d(a,c)
本記事では配列の距離として,ハミング距離とレーベンスタイン距離を紹介したいと思います.
ハミング距離
ハミング距離(Hamming distance)は長さが等しい2つの配列に対して定義される距離です.
2つの配列の文字を前から順に,1文字目同士,2文字目同士,といったように見比べます.そして,異なる文字の数がハミング距離となります.
例として「10111110」と「11011111」のハミング距離を見てみましょう.

1文字目から順に見ていき,文字が同じであれば「0」を,文字が異なっていれば「1」を足していくイメージです.そうすると異なる文字の個数になります.

今回の例だと 0 + 1 + 0 + 0 + 0 + 0 + 1 + 1 = 3 となり,ハミング距離は3です.
もうひとつ例を挙げます.
「walk」「work」の2つの単語のハミング距離を計算してみまましょう.
1文字目は「w」で一致,2文字目は「a」と「o」で不一致,3文字目は「l」と「r」で不一致,4文字目は「k」で一致するため,ハミング距離は2となります.
ハミング距離を数式で表すならば以下のようになります.
ハミング距離.
長さ n の配列 S,S' に関して,配列 S の i 番目の文字を s_i,配列 S' の i 番目の文字を s'_i と表すとすると,ハミング距離 d_{Hamming} は以下のように表される.
d_{Hamming}(S,S') = \sum_{n}^{i=1} 1 - \delta _{s_i, s'_i}
ただし,\delta _{s_i, s'_i} はクロネッカーのデルタであり, s_i = s'_i のとき \delta _{s_i, s'_i} = 1 となり,そうでない場合 \delta _{s_i, s'_i} = 0 となる.
配列の編集操作
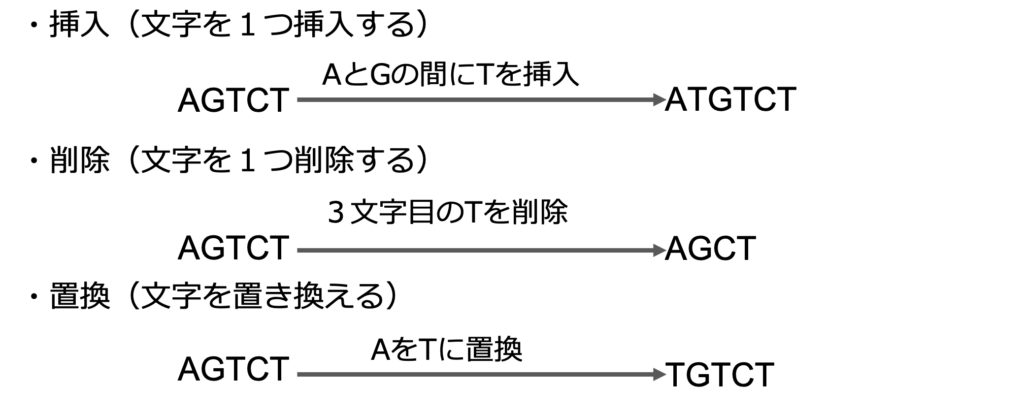
ここではレーベンシュタイン距離の解説の準備として,3種類の編集操作について解説します.
編集操作とは,配列の文字を変化させて別の配列にする操作のことです.
ここでは,挿入,削除,置換について解説します.
まず挿入ですが,配列に文字を1文字追加します.
例をいくつか挙げます.
- 配列「GTACCT」のGとTの間にAを挿入すると「GATACCT」となる.
- 「work」の末尾にsを挿入すると「works」となる.
- 「001101101」の4文字目の1と5文字目の0の間に1を挿入すると「0011101101」となる.
次に削除の操作について解説します.
削除の操作では,文字を1文字取り除きます.1種類ではなく1文字であることに注意が必要です.
削除の例もいくつか挙げてみます.
- 「GTTACC」の末尾のCを削除すると「GTTAC」となる.
- 「aisle」の先頭のaを削除すると「isle」となる.
- 「00001110」の末尾の0を削除すると「0000111」となる.
最後に置換の操作について解説します.
置換の操作では,1つの文字を別の文字に置き換えます.同じ文字であっても複数の文字を同時に変えることはできません.
置換についても例を挙げたいと思います.
- 「GTACGT」の最初のGをAに置換すると「ATACGT」となる.
- 「corporation」の3文字目のrをoに置換すると 「cooperation」となる.
- 「000101」の3文字目の0を1に置換すると「001101」となる.
ここまでに紹介した3つの編集操作,挿入,削除,置換について,以下の図にまとめたいと思います.
編集操作を用いる定ことで,ハミング距離を以下のように定義することもできます.
ハミング距離.
長さ n の配列 S,S' とする.ハミング距離 d_{Hamming} (S,S') は.置換の編集操作によって配列 Sを配列 S' に変換するときの,最小の置換回数である.
レーベンシュタイン距離
ハミング距離は,同じ長さの配列同士の距離でした.
異なる長さの配列の距離としてレーベンシュタイン距離(Levenshtein distance)1レーベンシュタイン編集距離(Levenshtein edit distance)を紹介します.
先ほど紹介した編集操作を用いてレーベンシュタイン距離を定義すると以下のようになります.
レーベンシュタイン距離.
配列 S を3つの編集操作,挿入,削除,置換によって配列 S' に変換することを考える.レーベンシュタイン距離 d_{Lev} (S,S') は.配列 S を配列 S' に変換するときの,最小の編集操作の回数である.
「work」を編集操作によって「walk」に変換することを考えます.
例えば,次のような変換方法があるでしょう.
「work」
↓ oを削除
「wrk」
↓ rを削除
「wk」
↓ wとkの間にa挿入
「wak」
↓ aとkの間にlを挿入
「walk」
この変換方法だと編集操作が4回必要となります.しかし,これは変換に必要な最小の編集操作の回数ではありません.次の変換方法を見てみましょう.
「work」
↓ oをaに置換
「wark」
↓ rをlに置換
「walk」
編集操作は2回です.ちなみにこれが最小回数となります.
よって「work」と「walk」のレーベンシュタイン距離は2となります.
さて,最小の編集操作の回数を求めるのに工夫が必要ですが,この記事では割愛します.
興味のある方は「レーベンシュタイン距離 動的計画法」で検索してみてください.2そのうち動的計画法の記事を書くかもしれません.
ちなみに,あえて再帰式で書くならば以下のようになります.
レーベンシュタイン距離.
X,Y を配列,x_1 を配列 X の先頭の文字,y_1 を配列 Y の先頭の文字,X' を配列 X の先頭の文字を除いた配列,Y' を配列 Y の先頭の文字を除いた配列とするとき,レーベンシュタイン編集距離 d_{Lev} の再帰式は以下のようになる.
d_{Lev} (X, Y) = \mathrm{min} =
\begin{cases}
d_{Lev} (X', Y) + 1 \\
d_{Lev} (X, Y') + 1 \\
d_{Lev} (X', Y') + 1 - \delta _{x_1, y_1}
\end{cases}
ただし,空配列 - に対して d_{Lev} (X, -) = |X| ( |X| は配列Yの長さ) ,d_{Lev} (- , Y) = |Y| ( |Y| は配列Yの長さ) ,d_{Lev} (- , -) = 0とする.また,\delta _{x_1, y_1} はクロネッカーのデルタであり, x_1 = y_1 のとき \delta _{x_1, y_1} = 1 となり,そうでない場合 \delta _{x_1, y_1} = 0 となる.
再帰式をそのままプログラムに起こすこともできますが,再帰式は2つの理由で悪手です.メモリも食いますし,何より配列が長いと計算時間が大きくなります.レーベンシュタイン距離を求めるコードを書くときも動的計画法を使うのが良いでしょう.