集合の基礎

この記事では，集合の基本的な内容について解説します．

集合とは何か

集合とは，数学的考察の対象となる「もの」の集まりのことです．

例えば，「1桁の自然数」「整数全体の集まり」「0 \leqq x \leqq 1を満たす実数 x の集まり」「平面上の点全体の集まり」「小文字のローマ字全体の集まり」「1次関数全体の集まり」は全て集合です．集合を記号で表すときは，一般的にA,B,X,Yなどの大文字のローマ字(ラテン文字)を使います．

集合を構成する「もの」ひとつひとつのことを要素もしくは元（げん）といいます． a が集合Aの要素であることを a \in A と書き，「 a は集合Aの要素である」または「 a は集合Aに属する」と読みます．逆に， a が集合Aの要素ではないことを a \notin A と書き，「 a は集合Aの要素ではない」または「 a は集合Aに属さない」と読みます．

集合は，どのような「もの」に対しても，その集合に属するか属さないかハッキリと定まっていなければなりません．例えば，「大きな数の集まり」は集合ではありません．「大きな数」は人によって感じ方が異なり，100を大きな数と感じる人もいれば，大きな数と感じない人もいるからです．

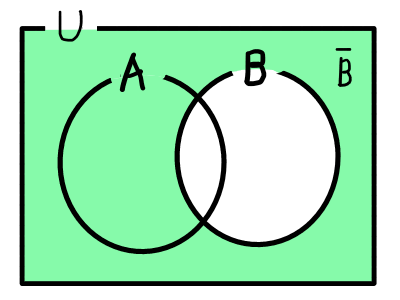
また，複数の集合の関係を視覚的に捉えるために，以下のような図が使われることがあります．このような図のことをベン図と呼びます．

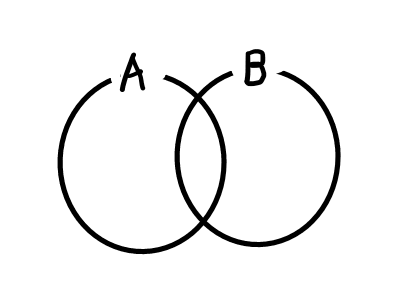
集合の記法

集合の書き方は2種類あります．

ひとつは要素を列挙する方法です．例えば，A= \{ 2, 4, 6, 8 \}やB= \{2,4,6,8, \cdots \}といった書き方です．基本的には全ての要素を書きますが，書ききれない場合，もしくは，要素が無限にある場合¹要素が無限にある集合を無限集合といいますが，どうやら学習指導要領外のようです．は，規則性が分かるところまで書いて，上記の集合Bのように残りの要素を省略します．このような記法を外延的記法といいます．

もうひとつの書き方は，その集合の要素が満たす条件を書く方法です．例を挙げますと，A= \{ x | 0 < x < 10 , xは偶数\}，B= \{ x | 0 < x , xは偶数\}といった具合です．代表となる要素を挙げ（今回の場合は x ）’|’の左側に書き，その文字が満たすべき条件を右側に書きます．このような記法を内包的記法といいます．

ちなみに，上で挙げた2つの例，集合 A ，集合 B は，書き方が違うだけで同じ集合を表しています．

さて，ここからは学習指導要領外の余談となります．
外延的記法には弱点が存在します．それは，規則性について誤解を生む可能性がある点です．要素が無限にある場合などに省略が発生しますが，この省略が誤解の原因となります．次の集合を見てください．

さて，これは一体どのような集合に見えますか？フィボナッチ数列²1つ前の数と2つ前の数を足していく数列．に出てくる数の集合に見えましたか？おやまあ、残念です．私は，以下の集合のつもりで書いていたのですが……

\{ x | x =\left \lceil \exp(\frac{n-1}{2}) \right \rceil，nは0より大きい整数\}

\lceil x \rceilは x 以上の最小の整数を意味する記号で，天井関数といいます． \exp(n)は e^n（ eはネイピア数）のことです．55の次が91であることまで書いておけば，フィボナッチ数列と間違えることは無かったのですが，やってしまいましたなぁ(棒読み)．

このように，外延的記法で書くと誤解が生じてしまうことがあります．要素が書ききれないほど多い場合は，内包的記法で書くことをオススメします．

お世話になったWebサイト様³フィボナッチ数列と途中まで等しい数列を探すのに使いました．この数列の存在自体は知っていたのですが，中身を思い出せなかったため調べてしまいました．このサイトはたまーにお世話になるので，ブックマークをオススメします．
オンライン整数列大辞典（OEIS）

部分集合

集合 A ， B に関して，全てのAの要素 a \in A に対して， a \in B が成り立つとき，AはBの部分集合であるといい， A \subset B と書きます．例えば， A = \{ 2, 4, 6, 8 \} ， B = \{ 2, 4, 6, 8, 10 \} のとき， Aの要素は全て B の要素であることから， A \subset B が成り立ちます．

集合 A ， B の要素が全て等しいとき，集合 A と集合 B は等しいといい， A = B と書きます．この定義は， A \subset B と B \subset A が同時に成り立つと言い換えることが可能です．

集合を扱う際には，考察の対象となる集合が，全てなんらかの集合の部分集合になる場合があります．整数の集合を考えているときは，考察対象となる集合は全て「整数全体の集合」の部分集合になりますし，平面上の点の集合について考えているときは，「平面上の点全体」の部分集合について考えていることになります．このように，考察の対象となる範囲が存在している場合，考察の対象全体の集合のことを全体集合，または普遍集合といいます．全体集合は英語の’universal set’の頭文字を取って，Uと表されることが多いです．

また，要素のない集合を空集合といい， \emptyset と書きます⁴外延的記法により \{　\} と書くこともできます．．空集合は，あらゆる集合の部分集合となります（任意の集合Aに対して， \emptyset \subset A ）．

和集合・共通部分・補集合

集合 A ， B に関して，集合 A ， B に共通する要素の集合を， A と B の共通部分といい， A \cap B と書きます．

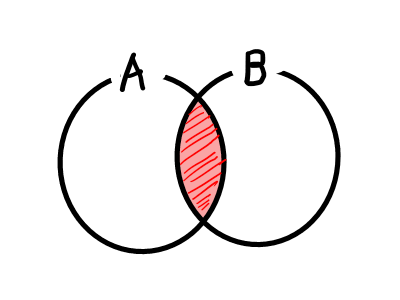
また，少なくともどちらか一方に属している要素の集合を和集合といい， A \cup B と書きます．

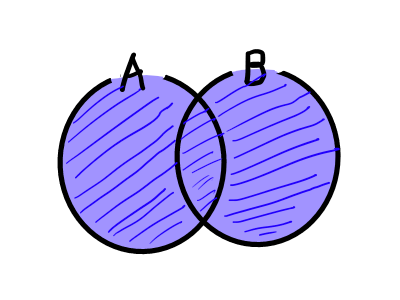
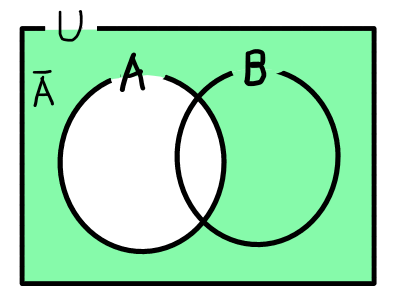
全体集合Uとその部分集合Aが与えられたときに，Aに属していない要素全体のことをAの補集合といい， \overline{A} と書きます⁵他の記号との兼ね合いで A^c や A' と書く場合もあります．．また，補集合に関して， \overline{ \overline{A}} = A， \overline{A} \cap A = \emptyset ， \overline{A} \cup A = U が成り立ちます．

ここまでに説明した，共通部分，和集合，補集合に関して，以下の法則，ド・モルガンの法則が成り立ちます．

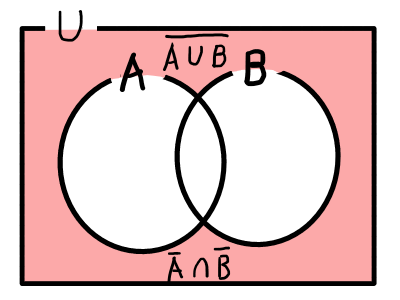
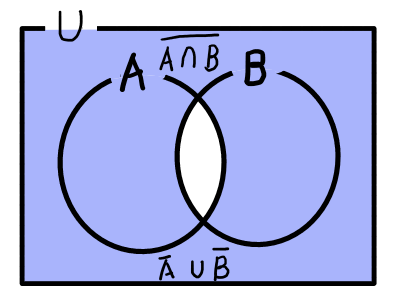
\overline{A \cup B} = \overline{A} \cap \overline{B} \\
\overline{A \cap B} = \overline{A} \cup \overline{B} 

ド・モルガンの法則はベン図を書くと納得すると思います．

厳密な証明の思い出

ここから最後まで余談になります．

私は大学時代にマンツーマンで数学のゼミをしていましたが，最初にぶつかった壁が厳密な証明でした．
自分としては集合の法則などは図を使って示せた気になっていたのですが，それは証明と呼べるものではありません．「集合が等しいこと」をしっかりと証明するならば，「左辺の集合の要素ならば，右辺の集合の要素でもある」( A \subset B )ことと「右辺の集合の要素ならば，左辺の集合の要素である」( B \subset A )を示す必要があります．「集合が等しいこと」の定義は何であるかに立ち返り，定義が「 A \subset B と B \subset A が同時に成り立つこと」であることを理解し，それを示す必要がある，というわけです．

初めは厳密な証明の意味がよく分かりませんでしたが，分かるようになってからは証明に夢中になりました．しかし，数学をするにあたって，厳密な証明は必要ですが，同時に，内容の論理的理解や感覚的理解を忘れてはいけません⁶幾何学の問題の幾何学的意味を理解できなかったにもかかわらず，代数的操作だけで幾何学の問題を解き続けた物理学者もいるので，感覚的理解が必ずしも必要かと訊かれると，「私は必要だと思う」としか応えられません．．
厳密な証明にのめり込んでいるときに，先生から「じゃあ，その例は？」などと質問され，ただちに答えられず，学習が偏っていたことにハッと気付かされたものです．
大学時代の数学ゼミは，厳密な証明の習得と感覚的理解との両立に手こずったことを覚えています．

ちなみに，厳密な証明の片鱗を味わいたい方は，赤チャート⁷改訂版　平成29年2月10日発行　第6刷の例題46，例題47，例題48に挑戦してみてください．

「勝手気ままに高校数学」シリーズ一覧へ