高校数学の理想的3ステップ勉強法！勉強方法に悩んでいる人は必見！3つの状況に合わせた実践法まで紹介！

　

　　

「数学の勉強方法が分からない」
「数学の成績を上げたい」
「数学を楽しく勉強できるようになりたい」

　　

高校数学をどう勉強すればいいか悩んでいるあなたへ．

　　

この記事では，数学の理想的な勉強方法の一例を紹介します．
人によって向き不向きがあります．万人に共通する勉強法はありませんが，出来るだけ多くの人に当てはまる理想的な勉強法を紹介したいと思います．

また定期試験の勉強なのか，大学入試に向けた勉強なのか，時間がどのくらい残されているのか，状況によって勉強方法も変わってきます．記事の後半では，状況ごとに理想的勉強法をどう実行すれば良いかを解説したいと思います．

　　　
↓本記事の要点↓

• 新しい数学的概念は，何も見ずに解説できるまで「理解」する．
• 公式や定理は自力で証明してみる¹例外あり．
• 演習問題はスラスラ解けるまで繰り返す．
• 時間がないときは，小手先の勉強法や暗記でOK！志望大学に合格することが最重要！
• あくまで勉強方法の１つなので，自分と勉強法の相性も大切に．

　　　　

理想的な高校数学の勉強方法

「理想的」の定義からしていきましょう．

この記事では，理想的な高校数学勉強法とは，

• 計算だけでなく，数学ができるようになる．
• 基本的な問題から応用問題まで対応できるようになる．
• 大学数学とのギャップを少なくする．
• 出来るだけ多くの人に当てはまる方法である．

以上の4つの条件を満たした勉強方法であるとします．

数学は「暗記科目」であると言われることがあります．ひどい場合ですと「数学は丸暗記だ」などと言われる場合もあります²ひどいWebサイトやブログになりますと，有名な数学者である岡潔の随筆『春宵十話』から「試験は全て暗記で済ませた」という文章を文脈を無視して引用し，数学は丸暗記だとする主張も散見されます．しかし，これは岡潔に関する理解不足，調査不足が如実に現れた暴論であり，わざと文脈を無視している可能性すらある偉人への冒涜とも言える発言です．文脈もわからぬ阿呆にはハッキリと記している部分を見せるほかありませんので，その部分を随筆集『情緒と創造』より引用しましょう．
（旧制中学1年から5年に関して）それで私には学科は暗記物と数学の二つしかなかった。数学はここでは「覚えなくてもよいもの」である。．しかしこれは本当でしょうか？私は数学は暗記科目ではないと考えています．確かに暗記が必要な部分もありますが，数学において重要なことは理解することだと思います．数学で初めて学ぶ概念を理解する，定理や公式を理解する，解答をしっかり理解して納得した上で書き上げる，これらが数学の土台だと考えています．

大学入試においても，理解を重視することは重要です．基本的な概念の理解が，応用問題の糸口になるときがあります．また近年では，基本的な概念の理解を直接質問する問題が増えています³1ラジアンの定義(弧度法の理解)や加法定理の証明など．

理解を重視することは数学を楽しむためにも重要なことです．
2022年にフィールズ賞⁴40歳以下の優秀な成果を挙げた数学者に贈られる賞を受賞したメイナードのインタビュー記事を引用したいと思います．

質問者：数学の面白さを理解してもらうにはどうしたらいいでしょうか？

メイナード氏：数学は計算ではなくアイディアであることを理解してもらうことが重要だと思います。

これは私が学生に教える際にも、心がけていることです。

数学嫌いこそ読んでほしい！　フィールズ賞を受賞した4人の数学者のインタビュー (3/4)
https://nazology.net/archives/111610/3　(2022年7月13日閲覧)

これは高校数学にも当てはまることでしょう．高校生の間は，自分でアイディアを出す機会は，上質な応用問題を解くときしかないかもしれません．しかし，新しく学ぶ概念，解答がどのようなアイディアに基づいているか理解することは，数学を楽しむための第1歩になるのです．

　

ただし，高校数学に「暗記要素」があることは否定できません．その理由は2つあります．
その理由のひとつは，高校数学には証明不可能な定理や，アイディアの理解すら困難な部分が存在するためです．極限については厳密な証明ができませんし，無限や連続性についてはまともな解説すらない場合があります．球の体積や表面積の公式は，数学Ⅲを学習しない人にとって，暗記が最も確実な習得方法でしょう．
もうひとつの理由は，定期試験や大学入試においては，早く解けることが有利に働くためです．特に大学入学共通テストや定期試験では，計算が早いこと，頻出する問題形式の解法を暗記することで，高得点が取りやすくなる場合があります．
これらのことが原因で，数学にも明確な暗記要素が存在しており，そのため数学は暗記科目であるという誤解が生まれているのでしょう．

　

さて事前の解説が長くなりましたが，これから理想的な高校数学の勉強方法を紹介していきます！

STEP1. 新しい概念を理解する

まず初めに，新しく出てきた概念を理解しましょう．

三角比を例にこのSTEPを簡単に解説します．
まず三角比は「相似な直角三角形の辺の比」が始まりのアイディアになります．どの２つの辺の比であるかによって，正弦，余弦，正接が定義されます．さらにこれらのアイディアから，直角三角形において適当な角の大きさと辺の長さが分かれば，他の辺の長さも計算できることが分かります．
しかし，直角三角形だけを使っていると，鈍角に対応できないため三角比の概念を拡張してやる必要があります．xy平面座標において原点を中心とする円を使って，正弦，余弦，正接の定義をし直します⁵詳しくは，こちらやこちらのページをご参照ください．．

上記のような内容をもう少し詳細に，何も見ずに説明できるようになればOKです．

また必要に応じて簡単な練習問題を解くのも良いでしょう．三角比の例の場合，\sin{60^{\circ}} や \tan{45^{\circ}} を求めるような練習をするのが良いでしょう．

　　

　　

[追記 2022年9月30日]

どうしても理解できない部分は丸暗記しても構いません．飛ばしても構いません．ただし，どの部分を丸暗記したか，どの部分を飛ばしたかを記録しておきましょう．

理解が困難な場合に限り，丸暗記は学習に必要なものだと考えています．というのも以下に示すようなプロセスが頻繁に起こるためです．

どうしても理解できない
↓
解答例や証明方法を見ても理解できない
↓
丸暗記（「飛ばす」という方法もアリ）
↓
学習を進める
↓
いつの間にか丸暗記した部分（飛ばした部分）が理解できるようになっている

[追記おわり]

　　　

後に紹介するSTEP2と合わせて，個人的には以下の『総合的研究 数学』シリーズでの学習がオススメです．ただし「何も考えずにすぐ分かる」ことを期待すると大火傷する本なので，その点には気を付けて下さい．
また，令和3年度入学者までに適用の学習指導要領に基づいた本となっています．
令和4年度以降に入学した方は，学習指導要領の違いに留意して下さい．

　　　

本を読むのが苦手な人には，スタディサプリがオススメです．
スタディサプリには，理解することに重きを置いた授業動画があります．また動画をダウンロードして，どこでも見ることができます．
自分のペースで学習することができるので，塾などで理解している部分の授業を聴きたくない人にもオススメです．自己分析と自己管理ができる人には，最良の教材となるでしょう．

受験生の2人に1人が利用する圧倒的なわかりやすさ！まずは無料でお試し。

STEP2. 基本的な定理（公式を含む）を理解する

証明できる公式や定理は，自力で証明するのが良いでしょう⁷本来「公式」は「式の形で表現される定理」を意味するため，公式と定理を並記するのはおかしいですが，まぁ気にせず読みましょう．．試験中にど忘れした場合も，落ち着いて公式や定理を導き出すことができます．技巧的な式変形が必要だったり，複雑になる場合もありますので，難しそうな定理では，証明の例を読んでから取り組んだので構いません．

ただし高校数学の知識で証明することができない定理がありますので，そういった定理(公式)は無理に証明する必要がありません．なんとなくそれが成り立ちそうなことが納得できれば良しとしましょう．

さらに，公式や定理をイメージで捉えることも重要です．

三角比の例ですと，余角定理や正弦定理，余弦定理，面積の公式を証明してみましょう⁸詳しくはこちらやこちらをご参照ください．．図を描けるものに関しては，図を描いてみるのもオススメです．

　　

　　　

STEP2の勉強においてオススメの本が『プレックス数学重要公式・定理集』です．文系版と理系版があります．重要な公式と定理を集めた一冊で，高校数学の知識で証明可能なものは全て証明が載っています．
厳密な証明ができないものに関しては説明という形で解説が載っているため，高校までの知識で証明可能か否かをキッチリ分けているという意味でもオススメの一冊です．

STEP3. 演習問題を解く

最後に演習問題を解くことで，理解を深めましょう．

間違えた問題は，どうして間違えたのかをしっかりと考えることで，誤解を解消したり，理解の浅い部分を見つけることができます．また問題を解くために必要な考え方を身につけることもできます．自分の誤答と向き合うのは勇気のいることですが，勉強をする上では必要不可欠なことです．頑張りましょう．

また，現実の世界に応用するタイプの文章問題を避ける人がいますが，このような問題もしっかりと解きましょう．三角比などの，大昔から現実に応用されてきた分野では，入試でもこのタイプの文章問題が出題されることがあります．特に大学入学共通テストでは，2年連続で三角比を現実の世界で使うことを想定した問題が出題されています．

　

　　

さてこのSTEP3ですが，もう一つ重要なポイントがあります．それは繰り返し問題を解くことです．大学以降の数学ですと，自力で解ける程度まで繰り返せば上出来ですが，高校数学の場合は，スラスラ解けるようになるまで繰り返すことが推奨されます．もちろん，問題の難易度や，現時点での習熟度，数学に充てられる勉強時間などを考慮して，繰り返す回数を決めましょう．

何度も繰り返すことには理由があります．高校数学は，定期試験や大学入試で高得点をとることが重要な目的のひとつであり，それらの試験では解く早さが重要な場合があるためです．本来，早く解けるからといってすごいワケでもナンデモナイのですが，そこは文句を言っても仕方がありません．そんな形式になっているのですから，それに合わせて勉強しましょう．

　　　

　　　　　

STEP3の学習には，問題集が必要となります．オススメの問題集はチャート式シリーズの通称『青チャート』です．チャート式数学には4つの色があり，難しい順に，赤→青→黄→白となっています⁹入試問題に特化した紫や黒もありますが，主にこの４色が有名です．．
『青チャート』が難しいと感じる人や数学に苦手意識がある人は，『黄チャート』を使用するのもアリだと思います．逆に『赤チャート』は，数学で確実に高得点を取りたい人や，すでに青チャートを解き終わっている人以外にはオススメしません．

↓令和3年度までに入学された方はこちらがオススメです．↓

　　

↓令和4年度以降に入学された方はこちら↓

　　

理想的な勉強方法，３つのステップのまとめ

この勉強法の3ステップをまとめると以下のようになります．

　　　　　

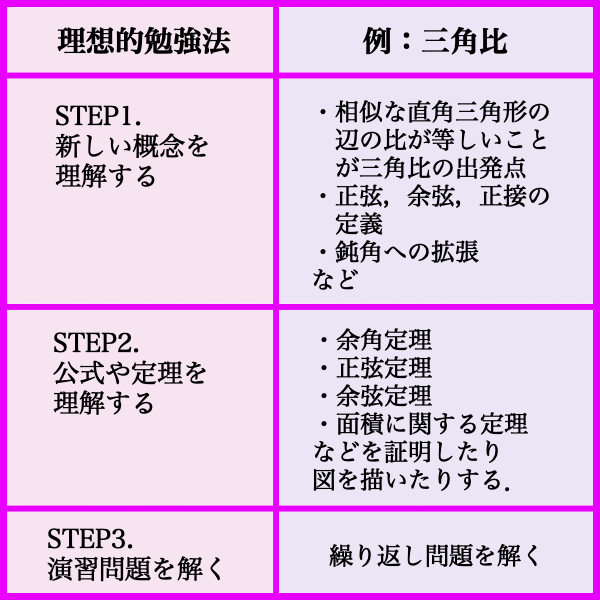
当たり前のことばかり書いていると思う人がいるかもしれません．
しかし，その当たり前が多くの人にとって重要なのです．

自分の状況に合わせた勉強をしよう！

さてこれまで理想的な勉強方法を解説してきましたが，常にこの勉強方法が最適であるとは限りません．
置かれている状況によって，この勉強法を多少アレンジしたり，理想論を投げ捨てて小手先に走ることが最適のケースもあります．

ここからは，状況に合わせた勉強方法について説明します．

初めに以下のフローチャートに沿って，現状がどのケースに当てはまるか確認しましょう．

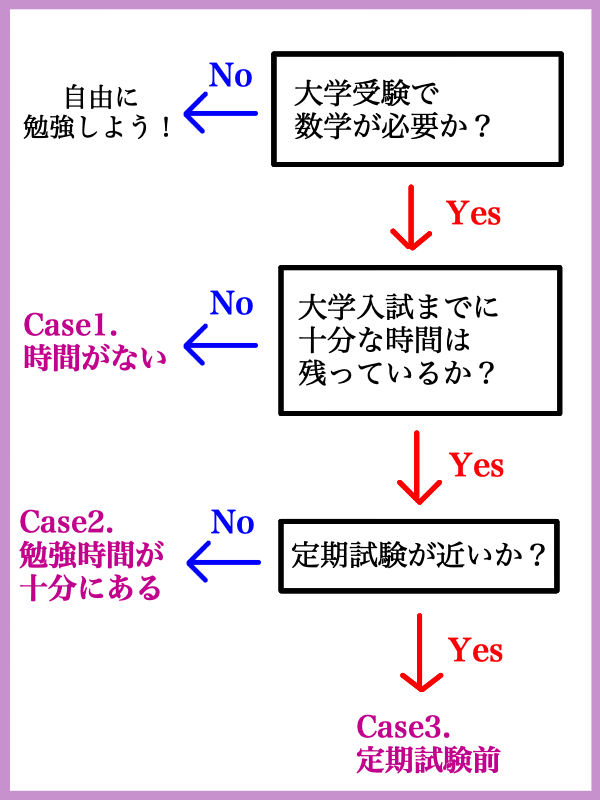
フローチャートの質問の補足
「大学入試までに十分な時間は残っているか？」と言う質問に関しては，
(未学習の単元&苦手な単元の数) × 1ヶ月 + 1ヶ月という式で必要な時間を概算してみてください．この時間と大学入学共通テストまでの残り日数を比較しましょう．
勉強する科目数が少なく，数学の勉強に時間を割ける人は「× 1ヶ月」の部分を「× 20日」に変えても構いません．ちなみに最後の「+ 1ヶ月」はマークシート形式に慣れるための時間です．マークシート形式の試験を受けない人は省きましょう．

状況別勉強方法を解説！

大雑把にではありますが，フローチャートで状況を整理しました．
ここからは，置かれている状況別に勉強方法を提案したいと思います．

Case1. 時間がない場合

時間がない場合，全ての単元をしっかりと勉強することは現実的ではありません．勉強する単元の取捨選択をしたり，一部の単元に勉強時間を偏らせる必要があります．

このケースでは，過去問を出来るだけ早く利用し始めましょう．
志望校が決まっていない場合は，出来るだけ早く志望校を決めてください．もちろん滑り止めも含めて決めましょう．

赤本などの過去問集には，各科目の問題の特徴や出題傾向のページがあります．まずはそれを見て，重点的に勉強する単元を決めましょう．実際の問題を見てみることも重要です．大学によって，問題の感覚的な特徴も異なるので，自分に合いそうなもの，点を取れそうな単元・分野を肌感覚で探しましょう．こういった直感は意外と重要です．

しっかり学習する単元，少しだけ勉強する単元，全く勉強しない単元を決めて，それに従って勉強しましょう．

少ししか勉強しないと決めた単元の勉強では，理想論もくそもありません．理解するよりも公式丸暗記の方が楽だと感じたら，直ちにそうしてください．本当に残り時間が少ない場合も同様です．
理想論を投げ捨てて，小手先の勉強方法に走ることになったとしても，志望校に合格できればひとまずOKなので，数学との付き合い方は大学合格が決まってから考えましょう．

Case2. 勉強時間が十分にある場合

上述した理想的な勉強方法で勉強することをオススメします．

どの科目にも言えることですが，時間が十分にあるときに，土台となる部分をしっかり作っておきましょう．

Case3. 定期試験前

定期試験前も，上述した理想的な勉強方法をオススメします．

ただし，それまでに十分な学習ができている場合や，残り時間が少ない場合は，各STEPの勉強がうまくいっているか，確認するだけで十分でしょう．

STEP1の場合，新しく学習した数学的概念について，何も見ずに解説できるか試してみましょう．
STEP2については，公式を覚えているか，忘れた場合に備えて公式を自力で導出できるか確認します．
STEP3については，それまでに解いた問題のうち間違えた問題の確認を優先しましょう．余裕があれば，まだ解いたことのない問題を解くのもアリです．

ちなみに，定期試験対策でもスタディサプリがオススメです．

最後に

高校数学の理想的な勉強方法と，状況に合わせた勉強方法について解説しました．

終盤でこのようなことを言うのもなんですが，人によって合う合わないの相性があると思いますので，1ヶ月試してみて合わないなと感じたら，自分なりの勉強方法を考えてみましょう．また少しだけアレンジを加えたい人もいると思います．自分に合った勉強方法を考えることもまた，重要な勉強です．積極的に挑戦してみましょう．

最後にこの記事のポイントを再掲して終わりたいと思います．それでは，数学の勉強を楽しみましょう！

• 新しい数学的概念は，何も見ずに解説できるまで「理解」する．
• 公式や定理は自力で証明してみる¹⁰例外あり．
• 演習問題はスラスラ解けるまで繰り返す．
• 時間がないときは，小手先の勉強法や暗記でOK！志望大学に合格することが最重要！
• あくまで勉強方法の１つなので，自分と勉強法の相性も大切に．

　　　

「勝手気ままに高校数学」シリーズ一覧へ